初中 数学
 ,如图所示.将函数y=kx+b中的k与b交换位置后得一次函数y=bx+k,其图象为直线
,如图所示.将函数y=kx+b中的k与b交换位置后得一次函数y=bx+k,其图象为直线  .设直线
.设直线  交y轴于点A,直线
交y轴于点A,直线  交直线
交直线  于点B,直线
于点B,直线  交y轴于点C.
交y轴于点C. | x | ﹣2 | 4 |
| y | ﹣4 | 2 |

-
(1) 求直线l2的解析式;
-
(2) 若点P在直线
 上,且△BCP的面积是△ABC的面积的1+
上,且△BCP的面积是△ABC的面积的1+  倍,求点P的坐标;
倍,求点P的坐标;
-
(3) 若直线y=a分别与直线
 ,
,  及y轴的三个交点中,其中一点是另两点所成线段的中点,求a的值.
及y轴的三个交点中,其中一点是另两点所成线段的中点,求a的值.
 B .
B .  C .
C .  D .
D . 


-
(1) 求a2+b的值;
-
(2) 求代数式3abc-a2b-[3a2b-(ab2-3abc)+ab2]的值.
(几何概型)
条件:如图1:  是直线
是直线  同旁的两个定点.
同旁的两个定点.
问题:在直线  上确定一点
上确定一点  ,使
,使 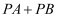 的值最小;
的值最小;
方法:作点  关于直线
关于直线  对称点
对称点 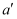 ,连接
,连接  交
交  于点
于点  ,则
,则  ,
,
由“两点之间,线段最短”可知,点  即为所求的点.
即为所求的点.

-
(1) (模型应用)
如图2所示:两村
 在一条河
在一条河  的同侧,
的同侧,  两村到河边
两村到河边  的距离分别是
的距离分别是  千米,
千米,  千米,
千米,  千米,现要在河边
千米,现要在河边  上建造一水厂,向
上建造一水厂,向  两村送水,铺设水管的工程费用为每千米20000元,请你在
两村送水,铺设水管的工程费用为每千米20000元,请你在  上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用
上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用 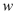 .
. -
(2) (拓展延伸)
如图,
 中,点
中,点  在边
在边  上,过
上,过  作
作  交
交  于点
于点  ,
,  为
为 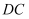 上一个动点,连接
上一个动点,连接  ,若
,若  最小,则点
最小,则点  应该满足( )(唯一选项符合题意)
应该满足( )(唯一选项符合题意) A .
A . B .
B .  C .
C .  D .
D . 
男生:100,95,95,90,90,90,85,85,80,80;
女生:100,95,95,90,90,90,90,85,85,80.
-
(1) 完善分析数据表,并写出女生成绩方差的计算过程.
平均分
中位数
众数
方差
男生
89
90
39
女生
90
-
(2) 由分析数据,评估这个班男生、女生选手成绩.
 的三个顶点的坐标分别是
的三个顶点的坐标分别是 ,
,  ,
,  .
.
-
(1) 直接写出点A、B、C关于x轴对称的点
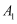 、
、 、
、 的坐标;
的坐标;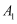 (,)、
(,)、 (,)、
(,)、 (,)
(,)
-
(2) 在图中作出
 关于y轴对称的图形
关于y轴对称的图形 .
.
-
(3) 求
 的面积.
的面积.
 =1﹣
=1﹣  ;②
;②  =
=  ﹣
﹣  ;③
;③  =
=  ﹣
﹣  ;④
;④  =
=  ﹣
﹣  ,…
,…
-
(1) 试用字母n的等式表示出你发现的规律,并证明该等式成立;
-
(2)

+
 +
+  +…+
+…+  =.(直接写出结果)
=.(直接写出结果)
 的结果是( )
的结果是( )
 B .
B .  C .
C .  D .
D . 
 在
在  的延长线上,
的延长线上, 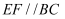 ,
,  ,
,  ,
,  ,则∠
,则∠  的度数是( )
的度数是( ) 
 B .
B .  C .
C .  D .
D . 
如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )

已知线段AB的长为10厘米,点P是线段AB的黄金分割点,那么较长的线段AP的长等于 厘米.(结果保留根号)
下列说法中正确的是( )
(A) 方程3x-4y=1可能无解.
(B) 方程3x-4y=1有无数组解,即x,y可以取任何数值.
(C) 方程3x-4y=1只有两组解,两组解是:
(D) ![]() 是方程3x-4y=1的一组解.
是方程3x-4y=1的一组解.
如图所示,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形![]() 绕坐标原点
绕坐标原点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后得到四边形
后得到四边形![]() .
.
(1)直接写出![]() 点的坐标;
点的坐标;
(2)将四边形![]() 平移,得到四边形
平移,得到四边形![]() ,若
,若![]() ,画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)
,画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)

二次函数![]() 与一次函数
与一次函数![]() 的图象如图所示,则满足
的图象如图所示,则满足
![]() 的x的取值范围是
的x的取值范围是
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]()
 |
- —I feel stressed from time to time. What can I do with it?
- 原来静止的氡核在进行衰变时,放出的粒子具有动能,设此过程中核能均转化为粒子动能,(1)求出α衰变过程中氡核剩余核动能 (
- 细胞核中行使遗传功能的重要结构是A.核被膜及核孔B.球状结构的核仁C.染色质D.透明、胶状的核基质
- 如图所示,在y=0和y=2m之间有沿着x轴方向的匀强电场,MN为电场区域的上边界,在x轴方向范围足够大。电场强度的变化如
- C、H、 O 三种元素在人体内质量分数约为73%左右,而在组成岩石圈的化成分中还不到1%,这一事实说明了( )A.生
- 如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米, ∠CAB=30°,∠CBA=45°,因线路整改需要,将
- Only by working hard and never giving up our goals. A.
- 有一动圆P恒过定点F(a,0)(a>0)且在与y轴相交与点A、B,若△ABP为正三角形,则点P的轨迹为( ) A.
- Tom is verykind and I promise you will get onwell hi
- 若NA表示阿伏加德罗常数的值,下列叙述正确的是 ( ) ①标准状况下,2.24 L四氯化碳含碳原
- 如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那
- , ,无人会,登临意。(辛弃疾《水龙吟·登建康赏心亭》)
- A、B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,
- 补写出下列题目中的空缺部分: 31.王维《送元二使安西》中有“劝君更尽一杯酒,西出阳关无故人”两句诗,高适《别董大》中
- —Where isSally from , Mike ? — A .I am from C
- 下列有关溶液中离子存在和转化的表达合理的是( ) A. 向0.1 mol·L-1、pH=1的NaHA 溶液中加入 NaO
- 下列搭配正确的是( ) A、古埃及——西亚——金字塔 B、古巴比伦——北非——《汉谟拉比
- 下列试纸使用时,不宜先用水湿润的是 A.蓝色石蕊试纸 B.红色石蕊试纸 C.pH试纸 D.淀粉碘化钾试纸
- 著名学者汉斯·科恩认为,普鲁士19世纪60、70年代的胜利,“为1918年和1945年的失败打下了基础”。以下各项可以作
- 双曲线的离心率为,且它的两焦点到直线的距离之和为2,则该比曲线方程是 A. B. C.



