初中 数学
 人,则有
人,则有  人无法安排;每间住
人无法安排;每间住  人,则空出
人,则空出  张床.
张床.
-
(1) 本次参加“冰雪冬令营”的学生总数为多少人?
-
(2) 冬令营结束时,学校准备给这些同学每人送一个售价为
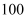 元的
元的  或
或  种纪念品,但实际购买时发现,
种纪念品,但实际购买时发现,  、
、  两种商品的售价都有变动,
两种商品的售价都有变动,  种商品打八折出售,
种商品打八折出售,  种商品的价钱比原售价提高了
种商品的价钱比原售价提高了 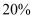 ,若实际购买
,若实际购买  种商品费用比购买
种商品费用比购买  种商品费用的
种商品费用的  倍多
倍多  元,那么此次活动中学校购买
元,那么此次活动中学校购买  种商品多少个?
种商品多少个?
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴(同角的补角相等)①
∴(内错角相等,两直线平行)②
∴∠ADE=∠3()③
∵∠3=∠B()④
∴(等量代换)⑤
∴DE∥BC()⑥
∴∠AED=∠C()⑦


 化简结果正确的是( )
化简结果正确的是( )
 B .
B .  C .
C . 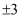 D .
D . 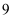
 =
= 
 有意义的字母x的取值范围是( )
有意义的字母x的取值范围是( )
 盒中的44号奖券调换到B盒,此时,A、C两盒奖券的编号平均数比调换前增加了0.6,B盒奖券的编号平均数比调换前增加了0.9,同时经计算发现,B盒中编号平均数调换前低于36,调换后编号平均数却高于36,则调换前A盒中有张奖券.
盒中的44号奖券调换到B盒,此时,A、C两盒奖券的编号平均数比调换前增加了0.6,B盒奖券的编号平均数比调换前增加了0.9,同时经计算发现,B盒中编号平均数调换前低于36,调换后编号平均数却高于36,则调换前A盒中有张奖券.


 的解集是x<2,那么m的取值范围是( )
的解集是x<2,那么m的取值范围是( )

-
(1) 填表:
顶点数a
棱数b
面数c
图1
8
12
6
图2
图3
图4
图5
-
(2) 若顶点数,棱数,面数分别用a,b,c表示,请你猜测a,b,c之间满足怎样的数量关系?请直接写出你的结论.
如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为.

| 时间/时 | 0 | 4 | 8 | 12 | 16 | 20 | 24 |
| 水位/米 | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 |
-
(1) 3(2x+5)>2(4x+3)
-
(2)
 ≥1
≥1
-
(3)
 =1
=1

 .
.
如图,点 














A . 3 B . 4 C . 

已知:如图,抛物线![]() 与
与![]() 轴交于点A(
轴交于点A(![]() ,0)和点B,将抛物线沿
,0)和点B,将抛物线沿![]() 轴向上翻折,顶点P落在点P'(1,3)处.
轴向上翻折,顶点P落在点P'(1,3)处.
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P'作![]() 轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比
轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比![]() (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:![]() ,
,![]() ,结果可保留根号)
,结果可保留根号)

如图,点M、N分别是正五边形ABC![]() DE的边BC、CD上的点,且BM=CN,AM交BN于点P.
DE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
 |
下列图形中,是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
- “Made in China” has changed Many shoppers in the Weststill
- They had all children well looked after ____ their parents r
- (2010·黑龙江省哈尔滨市,3,3分)下面句子中加点词语使用正确的一项是( ) A.周围高高低低的树木鳞次
- “这些事情(指东欧剧变)来得虽很突然,但都有长期形成的多方面的深刻原因。”就外部因素而言,东欧剧变是由于( )①照
- 函数的部分图像如图所示,则的值为 A B C D
- 条件甲:>1,条件乙:<a2(0<a<1),则甲是乙成立的( ) A.充分不必要条件
- 基因型为AaBb的个体,能产生几种配子 A.数目相等的四种配子 B.数目两两相等的四种配子 C.数目相等的两
- 阅读下面的文言文,完成小题。 廖永忠,楚国公永安弟也。从永安迎太祖于巢湖,年最少。太祖曰:“汝亦欲富贵乎?”永忠曰:“获
- 选择一种溶剂将碘水中的碘萃取出来,这种溶剂应具备的性质是( ) A.易溶于水,且不能与碘发生化学反应
- 已知反应3Cl2+6NaOH=5NaCl+NaClO3+3H2O,对该反应的下列说法不正确的是A、Cl2既是氧化剂,又是
- 2011年5月,在北京开幕的中国首届华佗文化节,集中展示了传统中医的优秀成果。下列属于华佗医学成就的有 ①编著《
- (4分)为了探究可燃物燃烧的条件,按如右图的甲、乙两个装置进行对比实验。请回答: (1)实验过程中,装置甲热水中的白磷
- 补出下列名句名篇中的空缺 (1)默写《书愤》的颔联。 ,
- 写出一个比大的负数: 。
- ---Whydidn’t you call me this morning? ---I _____call you.
- 设平面上向量与不共线, ⑴证明向量与垂直 ⑵当两个向量与的模相等,求角.
- 下图为某地等高线图,读图回答下面试题。图幅范围内的最大高差H可能为 A.1500<H<2000 B.100
- 2003年全国部分省份爆发流行的非典型肺炎主要是由于冠状病毒感染引起的,它与大肠杆菌的最明显区别是 A.无成形的细胞核
- 神经纤维受到刺激后会产生动作电位并沿神经纤维传导。下列叙述正确的是 A.神经纤维中段受刺激产生的动作电位是单向传导的 B
- 关于声现象,下列说法错误的是( ) A.弦乐队在演奏前,演奏员要调节乐器的弦的松紧,这样做的目的是为了改变音调 B



