初中 数学
如图,分别以AB,AC为直径的两个半圆,其中AC是半圆O的一条弦,E是弧AEC中点,D是半圆ADC中点。若AB=12,DE=2
且AC>6,则AC长为( )

A . 6+  B . 8+
B . 8+  C . 6+2
C . 6+2  D . 8+2
D . 8+2 
 B . 8+
B . 8+  C . 6+2
C . 6+2  D . 8+2
D . 8+2 
Rt△ ABC 中, AB=AC,点 D 为 BC 中点.∠ MDN=90°, ∠ MDN 绕点 D 旋转,DM、DN 分别与边 AB,AC 交于 E,F 两点.下列结论:① BE+CF=  BC;② S△AEF ≤
BC;② S△AEF ≤  S△ABC;③ S四边形AEDF=AD•EF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
S△ABC;③ S四边形AEDF=AD•EF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
 BC;② S△AEF ≤
BC;② S△AEF ≤  S△ABC;③ S四边形AEDF=AD•EF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
S△ABC;③ S四边形AEDF=AD•EF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
A . 1个
B . 2个
C . 3个
D . 4个
如图,下列选项中能使平行四边形ABCD是菱形的条件有( )
①AC⊥BD ②BA⊥AD ③AB=BC ④AC=BD.

A . ①③
B . ②③
C . ③④
D . ①②③
如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.求四边形ABCD的面积.

已知关于  ,
,  的二元一次方程组
的二元一次方程组  的解互为相反数,则
的解互为相反数,则  的值是( )
的值是( )
 ,
,  的二元一次方程组
的二元一次方程组  的解互为相反数,则
的解互为相反数,则  的值是( )
的值是( )
A . 3
B . 2
C . 1
D . 0
下列说法正确的是( )
①  +
+  =0;
=0;
②若  +2
+2  =0,则m=1;
=0,则m=1;
③无理数是无限小数;
④实数与数轴上的点一一对应.
A . ①②④
B . ②③④
C . ①③④
D . ①②③④
我市在创建全国文明城市过程中,决定购买A , B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
-
(1) 求购买A , B两种树苗每棵各需多少元?
-
(2) 考虑到绿化效果和资金周转,购进A种树苗不能少于48棵,且用于购买这两种树的资金不能超过7500元,若购进这两种树苗共100棵,则有哪几种购买方案?
-
(3) 某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
如图,在方格纸中,点A,B,C都是格点.

-
(1) 求tan∠BAC.
-
(2) 仅用直尺在图中画一个与∠BAC相等的角,使点B或点C是这个角的顶点,且BC为这个角的一边.(画出一个角即可)
如图,在平面直角坐标系中,双曲线  在第一象限的分支经过
在第一象限的分支经过  的直角顶点
的直角顶点  平行
平行  轴,当顶点
轴,当顶点  能同时落在双曲线
能同时落在双曲线  上时,
上时,  的值是.
的值是.
 在第一象限的分支经过
在第一象限的分支经过  的直角顶点
的直角顶点  平行
平行  轴,当顶点
轴,当顶点  能同时落在双曲线
能同时落在双曲线  上时,
上时,  的值是.
的值是.

计算:
-
(1)

-
(2)

-
(3)

在算式3-|-1□2|中的“□”里,选择一个运算符号,使得算式的值最大( )
A . +
B . -
C . ×
D . ÷
如图,

-
(1) 在△ABC中,BC边上的高是;
-
(2) 在△AEC中,AE边上的高是;
-
(3) 在△FEC中,EC边上的高是;
-
(4) 若AB=CD=2 cm,AE=3 cm,求△AEC的面积及CE的长.
如图,在四边形  中,AD
中,AD  BC,
BC,  .对角线
.对角线  交于点
交于点  平分
平分  交
交  于点
于点  ,连接
,连接  .
.
 中,AD
中,AD  BC,
BC,  .对角线
.对角线  交于点
交于点  平分
平分  交
交  于点
于点  ,连接
,连接  .
. 
-
(1) 求证:四边形
 是矩形;
是矩形;
-
(2) 若
 ,
,  =
=  ,求△
,求△  的面积.
的面积.
如图, 平行四边形ABCD的对角线  与
与  交于点
交于点  ,
,  ,
,  ,
, 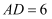 ,则
,则  的长为.
的长为.
 与
与  交于点
交于点  ,
,  ,
,  ,
, 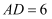 ,则
,则  的长为.
的长为.

已知二次函数y=x2+6x+c(c为常数)的图象与x轴的一个交点为(﹣1,0),则它与x轴的另一个交点的坐标是.
已知点A(1,![]() +2)在双曲线
+2)在双曲线![]() 上.则
上.则![]() 的值为( )
的值为( )
A. 1 B. -1 C. 2 D. -2
如图,已知正方形纸片ABCD,M,N分别是AD、BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ= 度.
 |
某学校初三年级男生共200人,随机抽取10名测量他们的身高为(单位:cm):
181、176、169、155、163、175、173、167、165、166.
(1)求这10名男生的平均身高和上面这组数据的中位数;
(2)估计该校初三年级男生身高高于170cm的人数;
(3)从身高为181、176、175、173的男生中任选2名,求身高为181cm的男生被抽中的概率.
如图,⊙O的半径为![]() ,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为( )
,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
 | |||
| |||
计算:![]() .
.
最近更新
- 如图是小明用八块小正方体搭的积木,该几何体的俯视图是( )
- 语法选择One day, a lady on a carriage saw a young man walking on
- 某学生欲称取4.3g氯化钠,他在左盘放了4g砝码,把游码移到0.3g处,然后在右托盘上加氯化钠直到天平平衡。这时托盘上的
- The story shows that ________knowledge of ________ first aid
- 某样本方差的计算式为S2 =[(x1-30)2+(x2-30)]2+…+(xn-30)2],则该样本的平均数=
- 下列关于物质、运动、规律三者关系说法正确的是( ) A.运动是物质固有的属性和存在方式 B.物质是运动的物质,运动
- 下列化工生产过程中,未涉及氧化还原反应的是( ) A.氨碱法制碱 B.氯碱工业 C.海水提镁
- 将pH=2的盐酸和pH=12的氨水等体积混合后,在所得的混合溶液中,下列关系式正确的是() A.c(Cl-)>c(NH)
- 在各项均为正数的等比数列{an}中,若a5·a6=27,则log3a1+log3a2+…+log3a10等于()
- 人民代表大会和其他国家机关(行政机关和司法机关)是监督和被监督的关系。
- 小球由地面竖直上抛,上升的最大高度为H,设所受阻力大小恒定,地面为零势能面.在上升至离地高度h处,小球的动能是势能的2倍
- 过点作圆:的切线,直线:与直线平行,则直线与的距离为( ) A.4 B.2 C. D.
- 实验室配制500 mL 0.2 mol·L-1的Na2CO3溶液,请完成下列问题: (1)应用托盘天平称取Na2CO3·
- 18.有甲、乙两种商品,经销这两种商品所能获得的利润分别是万元和万元,它们与投入资金万元的关系为:,今有3万元资金投入经
- 氯气与金属锡在加热时可制得SnCl4 ,SnCl4的熔点为-33℃,沸点为 114℃。SnCl4 极易水解,在潮湿的空气
- 已知 ||=1,||=。(1)若//,求・;(2)若,的夹角为135°,求 |+| .
- 下列遗传实例中,属于性状分离现象的是 () ①高茎豌豆与矮茎豌豆杂交,后代全为高茎豌豆 ②高茎豌豆与矮茎豌
- 下列属于公民直接参与选举的有( ) ①县及县级以下的人大代表的选举 ②县级以上各级人大代表的
- 读东北地区年降水量分布图(单位:mm),完成下题。 3.影响东北地区年降水量分布的主要因素有( ) A.太阳辐射
- 10月23日(星期五)中午在你上学途中发生了一件事情。请根据下列图画用英语写一篇日记。注意:(1)日记须包括所有图画的内



