初中 数学
 有两个相等的实数根,则m=.
有两个相等的实数根,则m=.


| 抽取件数(件) | 50 | 100 | 150 | 200 | 500 | 800 | 1000 |
| 合格频数 | 48 | 98 | 144 | 193 | 489 | 784 | 981 |
 ×4)之值为何?( )
×4)之值为何?( )
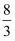 D . ﹣
D . ﹣ 
 )(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( ) 
 B .
B .  C .
C .  D .
D . 
-
(1)
 ;
;
-
(2)
 .
.

 中,点
中,点  分别是
分别是  的中点,点F是
的中点,点F是  上一点,连接
上一点,连接  ,且
,且  ,若
,若  ,则
,则  .
. 
 与
与 轴交于点
轴交于点 , 点
, 点 的坐标分别是
的坐标分别是 , 与
, 与 轴交于点
轴交于点 . 点
. 点 在第一、二象限的抛物线上,过点
在第一、二象限的抛物线上,过点 作
作 轴的平行线分别交
轴的平行线分别交 轴和直线
轴和直线 于点
于点 、
、 . 设点
. 设点 的横坐标为
的横坐标为 , 线段
, 线段 的长度为
的长度为 .
. 
-
(1) 求这条抛物线对应的函数表达式;
-
(2) 当点
 在第一象限的抛物线上时,求
在第一象限的抛物线上时,求 与
与 之间的函数关系式;
之间的函数关系式;
-
(3) 在⑵的条件下,当
 时,求
时,求 的值.
的值.
某中学初三(1)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男、女生的人数之比为________.
我区实施新课程改革后,学生的自主学习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调査,并将调査结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调査了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
如图,绐正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为l的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2012次“移位”后,则他所处顶点的编号是 .


在△ABC中,∠A=40°(每空1分,证明6分).
(1)如图1,若两内角∠ABC,∠ACB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(2)如图2,若内角∠ABC,外角∠ACE的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(3)如图3,若两外角∠EBC,∠FCB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 .
(![]() 选择其中一种数量关系加以证明)
选择其中一种数量关系加以证明)

![]()
请写出一个解为-2的一元一次方程__________________________.
如图,∠BAC=90°,AD⊥BC,∠BAD=30°,则∠C的度数是( )

A.30° B.40°
C.50° D.60°
- 某小组为了研究光对豌豆发芽的影响,在两个花盆里种了豌豆,并设计如下表实验,应该是( ) 花盆 阳光 温度 水 A 向
- 下列叙述正确的是
- 端午节,民间有在屋中贴五毒图的民俗,以红纸印画五种毒物,再用五根针刺于五毒之上,即认为毒物被刺死,再不能横行了。这种民俗
- (2009四川卷理)(本小题满分12分) 为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省
- 基因在染色体上可以从下列哪个结论中得出 A. 基因和染色体都在细胞中 B. 基因和染色体的行为存在着明显的平行关系 C.
- 某地首创一种实名制、免费发放的文化惠民卡,市民持卡可以看电影、看演出、买书,只要在签约商户进行文化消费,就可以享受折扣、
- 下表是我国某区域四季平均降水量和各等级降水量(mm),表中各等级降雨包含其它降水形式。据此完成3~4题。降水量 微雨 小
- 在可逆反应中,平衡常数与反应进行的限度关系正确的是() A. K越大,反应程度越大 B. K越大,反应程度越小 C.
- 如果a的倒数是1,那么a2009等于( ) A.1
- 一列车的制动性能经测定,当它以标准速度20m/s在水平轨道上行驶时,制动后需40s才停下,现这列车正以20m/s的速度在
- 祖国大陆实现解放和统一的标志性事件是 ( )A.抗日战争胜利
- 国家工业和信息化部要求从去年7月1日起;所有在我国境内生产销售的计算机出厂时都要预装一款名为“绿坝—花季护航”的绿色上网
- ①某人射击一次,中靶;②从一副牌中抽到红桃A;③种下一粒种子发芽;④掷一颗骰子,出现6点.其中是随机现象的是______
- --- What were you up to when she dropped in ?---I _____ for
- 右图是制取和收集某气体的实验装置,该装置可用于() A.浓盐酸和二氧化锰反应制取Cl2 B.浓氨水和生石灰反应制取NH3
- 下列各组物质所属类型全部正确的是 A. 碱性氧化物:Na2O Na2O2 A12O3 B. 酸性氧化物:CO Si02
- 下列表格中各项分类都正确的一组是()纯净物 混合物 电解质 非电解质 A 生理盐水 明矾 液态KNO3 蔗糖 B CaO
- My newly-rented small apartment was far away from the centre
- 某粒子结构示意图如图所示,下列说法错误的是()若,则该粒子符号为 B. 若,则该粒子是原子 C. 若,则该粒子是阳离子
- 利用化学反应原理的相关知识,回答下列问题: (1)将一定量纯净的氨基甲酸铵置于密闭真空容器中(假设容器体积不变,固体试样



