初中 数学
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于.

在 中,
中,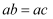 , 作AB的垂直平分线交AB于点D,交直线AC于点E,若
, 作AB的垂直平分线交AB于点D,交直线AC于点E,若 , 则∠B的度数为.
, 则∠B的度数为.
 中,
中,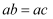 , 作AB的垂直平分线交AB于点D,交直线AC于点E,若
, 作AB的垂直平分线交AB于点D,交直线AC于点E,若 , 则∠B的度数为.
, 则∠B的度数为.
分解因式:
-
(1) 4﹣a2
-
(2) 3b2﹣12b+12
用反证法证明命题“在Rt△ABC中,若∠A=90°,则∠B≤45°或∠C≤45°“时,应先假设( )
A . ∠B>45°,∠C≤45°
B . ∠B≤45°,∠C>45°
C . ∠B>45°,∠C>45°
D . ∠B≤45°,∠C≤45°
若a与b互为相反数,c与d互为倒数,则(a+b)3﹣4(cd)5=.
《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,如图2所示,图中各行从左到右列出的算筹数分别表示未知数  ,
,  的系数与相应的常数项.图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为
的系数与相应的常数项.图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为  .
.
 ,
,  的系数与相应的常数项.图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为
的系数与相应的常数项.图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为  .
. 
图1
类似地,图2所示的算筹图我们可以表述为( )

图2
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式.
(2)当销售单价为多少元时,月销售额为14000元;
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
[参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是( ,
, )].
)].
化简  的结果是( )
的结果是( )
 的结果是( )
的结果是( )
A . -a-1
B . -a+1
C . -ab+1
D . -ab+b
如图,若∠DBC=∠D,BD平分∠ABC,∠ABC=50°,则∠BCD的大小为( )
A . 50°
B . 100°
C . 130°
D . 150°
如图,点 是
是 的内心,
的内心, 的延长线和
的延长线和 的外接圆相交于点
的外接圆相交于点 , 连接
, 连接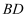 ,
,  ,
,  , 若
, 若 , 则
, 则 的大小为( )
的大小为( )
 是
是 的内心,
的内心, 的延长线和
的延长线和 的外接圆相交于点
的外接圆相交于点 , 连接
, 连接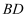 ,
,  ,
,  , 若
, 若 , 则
, 则 的大小为( )
的大小为( )
A . 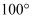 B .
B .  C .
C .  D .
D . 
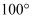 B .
B .  C .
C .  D .
D . 
一个不透明的盒子装有m个除颜色外完全相同的球,其中有4个白球,每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过如此大量重复试验,发现摸到白球的频率稳定在0.2左右,则m的值约为( )
A . 8
B . 10
C . 20
D . 40
过线段外一点画这条线段的垂线,垂足一定在( )
A . 线段上
B . 线段的端点上
C . 线段的延长线上
D . 以上情况都有可能
右图是某个几何体的三视图,则这个几何体是( )

A . 圆锥
B . 圆柱
C . 长方体
D . 三棱锥
阅读材料,回答问题:
小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= , AB=c=2,那么
, AB=c=2,那么 =
= =2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着
=2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着 =
= =
= 的关系.
的关系.

这个关系对于一般三角形还适用吗?为此他做了如下的探究:
-
(1) 如图2,在R△ABC中,∠C=90°,BC=a,AC=b,AB=C,请判断此时“
 =
= =
= ”的关系是否成立?答:
”的关系是否成立?答:
-
(2) 完成上述探究后,他又想“对于任意的锐角△ABC,上述关系还成立吗?”因此他又继续进行了如下的探究:
如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“
 =
= =
= ”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).
”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).
已知x+  =
=  ,则x-
,则x-  的值为( )
的值为( )
 =
=  ,则x-
,则x-  的值为( )
的值为( )
A .  B . ±2
C . ±
B . ±2
C . ±  D .
D . 
 B . ±2
C . ±
B . ±2
C . ±  D .
D . 
计算:(﹣1)0+|﹣1|=.
如图,在 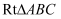 中,
中,  ,
, 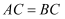 ,
,  轴,点
轴,点  、
、  都在反比例函数
都在反比例函数  上,点
上,点  在反比例函数
在反比例函数 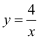 上,则
上,则  .
.
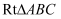 中,
中,  ,
, 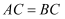 ,
,  轴,点
轴,点  、
、  都在反比例函数
都在反比例函数  上,点
上,点  在反比例函数
在反比例函数 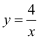 上,则
上,则  .
. 
如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=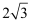 ,则四边形MABN的面积是()
,则四边形MABN的面积是()
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知x、y满足|x-5|+(x-y-1)2=0,则(x-y)2010的值是__________________.
比较大小:﹣5__________﹣3(填“<”、“>”、“=”)
最近更新
- 下列说法中,错误的是() A.无论是乙烯与Br2的加成,还是乙烯使酸性KMnO4溶液褪色,都与分子内含有碳碳双键有关 B
- 下列各组物质充分反应后,只能得到一种气体的是() A.固体硝酸铜受热分解 B.Na2O2与足量的稀硫酸反应 C.木炭和浓
- 实验室制取气体的装置如下图所示,根据所学知识,回答下列问题: (1)图中标有①②的仪器名称:①___________
- 请仿照示例,从下列列举的名著中选择其中的一部,写出该名著的作者,用一句话概括、点评名著的内容或特色。 举例:作者:施耐庵
- 据报道,意大利科学家用普通氧分子与带正电的氧离子作用,制造出新物质O4。下列关于化学键的叙述正确的是( )A.化学
- 如图所示,小球A、B带电量相等,质量均为m,都用长L的绝缘细线挂在绝缘的竖直墙上0点,A球靠墙且其悬线刚好竖直,B球悬线
- 我国著名生物学家童第周认为,搞生物学的人要学点辩证法,不懂辩证法就搞不好生物学。这一论断的合理性在于承认() A.哲学是
- 读“地球光照示意图”(题51图),完成下列问题。(10分)(1)图示为_________(节气),这一天大约是_____
- 、如图所示,请你用笔画线代替导线将开关和螺口灯座连入电路中,使开关能控制灯泡的亮灭.
- 下列甲、乙分裂过程中产生配子时发生的变异图解,请判断下列说法正确的是A.甲图中发生了基因突变,乙图中发生了基因重组 B.
- (2009·宁波中考)下列与实物图一致的电路图是( )
- 阅读下面的文字,完成1——3题。 情绪异常是一种非常复杂的现象,长期以来,各个领域的学者从自己的学科出发,对此现象纷
- The city of Yuyao has ___________in holding the 11th Exhibit
- 双链DNA分子的一个片段中,含有腺嘌呤520个,占碱基总数20%,则这个片段中含胞嘧啶( ) A.350个
- 2009年8月15日《人民日报》报道,河南南阳公民王清向全市181个政府部门申请信息公开,要求获知“三公”消费——公款吃
- (9分)如图13(1)所示,物体A、B的质量分别是4kg和8kg,由轻弹簧连接,放在光滑的水平面上,物体B左则与竖直墙壁
- 一正常女性与一色盲男性婚配,生了一个色盲女孩,这对夫妇的基因型是()A. XBXb、XBY B. XbXb、XbY C.
- SectionD Directions: Read the passage carefully. Then answer
- 对右边漫画中某地政府个别工作人员“钓鱼式执法”认识正确的是( )A.严格依照法律办事,维护了法律的权威 B.依法
- 针对多国涉足南海问题,中国《环球时报》社评严厉警告,所有和中国出现海上摩擦的周边国家如不加收敛,中国或将“杀一儆百”东亚



