初中 数学
如图,一次函数y=﹣  x+6与反比例函数y=
x+6与反比例函数y=  (k>0)交于A、B两点,过A、B两点分别作x轴、y轴的平行线交于点C,连接OC交AB于点D,连接OA.若△ADO的面积是△BDC面积的
(k>0)交于A、B两点,过A、B两点分别作x轴、y轴的平行线交于点C,连接OC交AB于点D,连接OA.若△ADO的面积是△BDC面积的  倍,则k的值是( )
倍,则k的值是( )
 x+6与反比例函数y=
x+6与反比例函数y=  (k>0)交于A、B两点,过A、B两点分别作x轴、y轴的平行线交于点C,连接OC交AB于点D,连接OA.若△ADO的面积是△BDC面积的
(k>0)交于A、B两点,过A、B两点分别作x轴、y轴的平行线交于点C,连接OC交AB于点D,连接OA.若△ADO的面积是△BDC面积的  倍,则k的值是( )
倍,则k的值是( ) 
A . 8
B . 10
C . 10.5
D . 12
长方形的周长为12cm,长是宽的2倍,则长为 cm.
⊙  的半径为5cm,AB、CD是⊙
的半径为5cm,AB、CD是⊙  的两条弦,
的两条弦,  ,
,  ,
,  .则
.则  和
和  之间的距离为.
之间的距离为.
 的半径为5cm,AB、CD是⊙
的半径为5cm,AB、CD是⊙  的两条弦,
的两条弦,  ,
,  ,
,  .则
.则  和
和  之间的距离为.
之间的距离为.
下列计算正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
利用幂的运算性质 计算:  .
.
 .
.
若 x=2+ , y=
, y= , 则x与y关系是( )
, 则x与y关系是( )
 , y=
, y= , 则x与y关系是( )
, 则x与y关系是( )
A . x>y
B . x=y
C . x<y
D . xy=1
如图,正方形 中,点E、F分别在边
中,点E、F分别在边 上,
上, , 则
, 则
 ;若
;若 的面积等于1,则
的面积等于1,则 的值是.
的值是.
 中,点E、F分别在边
中,点E、F分别在边 上,
上, , 则
, 则
 ;若
;若 的面积等于1,则
的面积等于1,则 的值是.
的值是.
如图,在平行四边形ABCD中,用直尺和圆规作的∠BAD平分线交BC于点E,若AE=8,AB=5,则BF的长为( )

A . 4
B . 5
C . 6
D . 8
解方程组.
-
(1)

-
(2)

先化简,再求值:已知 , 求
, 求 的值.
的值.
 , 求
, 求 的值.
的值.
如图,在△ABC中,∠ACB=90°,∠B=30°,CE垂直于AB于点E,D是AB的中点.

-
(1) 求证:AE=ED;
-
(2) 若AC=2,求DE的长.
某网店销售一种羽毛球拍和羽毛球,羽毛球拍每副定价80元,一桶羽毛球定价20元.“双十一”期间网店决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副羽毛球拍送一桶羽毛球;
方案二:买羽毛球拍或买羽毛球都按定价的90%付款.现某客户准备购买羽毛球拍10副,羽毛球  桶(
桶(  ),
),
-
(1) 若该客户按方案一购买,需付款元(用含
 的代数式表示)若该客户技方案二购买,需付款元(用含
的代数式表示)若该客户技方案二购买,需付款元(用含  的代数式表示);
的代数式表示);
-
(2) 若
 =30,通过计算说明按哪种方案购买较为合算?(用含
=30,通过计算说明按哪种方案购买较为合算?(用含  的代数式表示),
的代数式表示),
-
(3) 当
 =30时,你能给出一种更为省钱的购买方案吗?请写出你的购买方法,并计算需付款多少元?
=30时,你能给出一种更为省钱的购买方案吗?请写出你的购买方法,并计算需付款多少元?
如图,  平分
平分  ,
,  ,则
,则  ( )
( )
 平分
平分  ,
,  ,则
,则  ( )
( ) 
A .  B .
B .  C .
C . 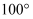 D .
D . 
 B .
B .  C .
C . 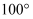 D .
D . 
如图,已知抛物线  与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
 与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3). 
-
(1) 求抛物线的解析式;
-
(2) 抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;
-
(3) 点P是抛物线上AC下方的一个动点,是否存在点p,使△PAC的面积最大?若存在,求出点P的坐标,若不存在,请说明理由.
如图,要使 成为矩形,需添加的条件是( )
成为矩形,需添加的条件是( )
 成为矩形,需添加的条件是( )
成为矩形,需添加的条件是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,顶点为(  ,﹣
,﹣  )的抛物线y=ax2+bx+c过点M(2,0).
)的抛物线y=ax2+bx+c过点M(2,0).

-
(1) 求抛物线的解析式;
-
(2) 点A是抛物线与x轴的交点(不与点M重合),点B是抛物线与y轴的交点,点C是直线y=x+1上一点(处于x轴下方),点D是反比例函数y=
 (k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.
(k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.
若  ,则
,则  的值为.
的值为.
 ,则
,则  的值为.
的值为.
若不等式  的解集中
的解集中  的每一个值,都能使关于
的每一个值,都能使关于  的不等式
的不等式  成立,则
成立,则  的取值范围是( )
的取值范围是( )
 的解集中
的解集中  的每一个值,都能使关于
的每一个值,都能使关于  的不等式
的不等式  成立,则
成立,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若![]() ,则
,则![]() 的值为_____.
的值为_____.
先化简,后求值:
![]() ,其中a=
,其中a=![]() +1.
+1.
最近更新
- 在平面直角坐标系中,点O为原点,点A的坐标为(-6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C
- 2011年3月11日,日本发生9.0级地震,地震引发海啸,多地被淹没,造成重大人员伤亡和财产损失。(1)氢在目前的地震预
- 有H、D、T三种原子,它们之间的关系是__________。 (1)在标准状况下,它们的单质的密度之比是________
- 下列化学用语与含义相符的是 A. ——1个铝离子带3个单位的正电荷 B.2H2O——2个水分子
- 蛋白质进行化学消化的场所有() A. 口腔,食道,胃 B.口腔,咽,胃 C. 口腔,咽,小肠
- 如图甲所示,物体以初速度v0冲上足够长的粗糙斜面,乙图中关于物体位移x与时间t关系的图象可能正确的是
- 下列有关化学用语表示正确的是 A.:可以表示氯化铵的电子式 B.:可以表示中子数为18的氯原子结构示意图 C.:可以表示
- 右图所示食物网存在于某相对封闭的生态系统,若甲(生产者)固定太阳能为N,能量传递效率为10%,则丁获得的能量 A.等于
- 七七事变是因日本驻军在北平附近宛平城外卢沟桥演习、无理挑衅引起。的。允许包括日本在内的帝国主义国家派兵驻扎北京到山海关铁
- 近年在汉堡发现了1691年出版的《论语》英译本,书的前言写着:“这位思想家的道德是无限辉煌的。”被赞誉的思想家是 A.孔
- 古诗文默写。(共8分) (1) 子曰:“岁寒, 。”(《子罕》)
- 下列属于旅游活动直接产生的环境问题是( ) A.台风过后,海边一些旅游设施遭到破坏 B.为改变“自古华山一条路”,近
- 二、文学类文本阅读(14分) 诗棺 张晓林 于之渔这个诗人,爱黄昏到野外去煮茶喝。茶壶里丢三五片竹叶——有
- A lot of teachers hate doodlers(乱写乱画的人)during classes. “
- Alex: Excuse me, I’m a journalist and I want to get some inf
- 如图,以平行四边形ABCD的边AB、BC、CD、DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺
- 秦朝统一后,废除六国货币,并严禁地方和私人铸钱。这本质上体现了( )A. 专制主义中央集权制度的确立 B.
- 某校为了了解高一1800名学生的体重情况,从中随机地抽取160名学生进行测量。下列说法正确的是( ) ①总体是18
- 以35 m/s的初速度竖直向上抛出一个小球.不计空气阻力,g=10 m/s2,以下判断正确的是() A.小球到最大高度时
- —What do you wear when you go out? —Well, it ____.A.chan



