下列命题中正确的是(        )

A. 命题“，  ”的否定是“”

B. 命题“为真”是命题“为真”的必要不充分条件

C. 若“，则”的否命题为真

D. 若实数，则满足的概率为.

已知、m是两条不同的直线，是个平面，则下列命题正确的是（    ）

A．若//，//, 则      B ．若，//, 则

．若，,则//      D ．若//，,，则

若 点的极坐标为 ，则 点的直角坐标是（ ）

已知点P是抛物线y²＝－8x上一点，设P到此抛物线准线的距离是d₁，到直线x＋y－10＝0的距离是d₂，则d₁＋d₂的最小值是(　　)

A.       B．2      C．6       D．3

某校高三（）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题．

（1）求全班人数及分数在之间的频数，并估计该班的平均分数；

（2）若要从分数在之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在之间的概率．

已知实数x、y满足2x＋y＋5＝0，那么的最小值为              .

椭圆的焦点在轴上，且，，则这样的椭圆的个数是

 若f（x）=﹣x²+bln（x+2）在（﹣1，+∞）上是减函数，则b的取值范围是（  ）

A．[﹣1，+∞）              B．（﹣1，+∞）   

C． （﹣∞，﹣1）          D．（﹣∞，﹣1]  

袋子中有四个小球，分别写有“幸”“福”“快”“乐”四个字，有放回地从中任取一个小球，取到“快”就停止，用随机模拟的方法估计直到第二次停止的概率：先由计算器产生1到4之间取整数值的随机数，且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字，以每两个随机数为一组，代表两次的结果，经随机模拟产生了20组随机数：

据此估计，直到第二次就停止的概率为(　　)

A.                          B.                  C.                               D.

在平面直角坐标系中，若不等式组(a为常数)所表示的平面区域的面积等于2，则a的值为         

已知点P，Q分别在直线与直线上，且，点，，则的最小值为（）．

A．           B．      C．            D．

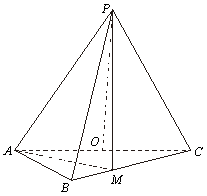
如图，在三棱锥中，，，为的中点．

（1）证明：平面；

（2）若点在棱上，且二面角为，求与平面所成角的正弦值．

 若﹁p是﹁q的必要不充分条件，则p是q的

A.充分不必要条件                B.必要不充分条件

C.充分且必要条件                D.既不充分也不必要条件

如图，在中，边上的中线长为3，且，．

（1）求的值；

（2）求及外接圆的面积．

已知等差数列{a_n}的公差为d(d≠0)，且a₃＋a₆＋a₁₀＋a₁₃＝32，若a_m＝8，则m为（   ）

A．12                 B．8 

C．6                  D．4

命题“，”的否定为                   ．

一个几何体的三视图如图所示，则该几何体的体积为(　　)

　　A． 　　　　  B．          C． 　　　　  D．

已知圆，圆，直线分别过圆心，且与圆相交于,与圆相交于,是椭圆上的任意一动点，则的最小值为            .

设命题p：已知点，直线与线段AB相交；命题q：函数的定义域为R。如果命题p、命题q有且仅有一个为真命题，求实数a的取值范围。

从某小学随机抽取名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图由图中数据可知身高在内的学生人数为（   ）

A.20          B.25            C.30             D.35