作图﹣旋转 知识点题库
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).

-
(1) 画出△ABC关于y轴对称的△A1B1C1;
-
(2) 将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留π).
(1)如图,▱ABCD中,E、F、G、H为各边中点,请用三种不同的方法,通过适当连线,找出▱ABCD的对称中心P.
(2)圆内接正五边形是否中心对称图形 .


-
(1) ①在图中,先将△AOB向上平移6个单位,再向右平移3个单位,画出平移后的△A1O1B1;(其中点A,O,B的对应点为A1 , O1 , B1)
②在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1 , B1的对应点为A2 , B2)
-
(2) 直接写出点A2 , B2的坐标.

-
(1) 画出△ABC关于x轴对称的△A1B1C1 .
-
(2) 画出△ABC绕原点O旋转180°后的△A2B2C2 .

(I)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1 , 请画出菱形OA1B1C1 , 并直接写出点B1的坐标;
(II)将菱形OABC绕原点O顺时针旋转90°菱形OA2B2C2 , 请画出菱形OA2B2C2 , 并求出点B旋转到点B2的路径长.
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)

-
(1) 画出△ABC关于y轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;
-
(2) 画出△ABC绕点A按逆时针旋转90°后的△AB2C2 , 并写出点C的对应点C2的坐标.

 只是轴对称图形而不是中心对称图形;
只是轴对称图形而不是中心对称图形;
 既是轴对称图形又是中心对称图形.画出符合要求的图形各两个.
既是轴对称图形又是中心对称图形.画出符合要求的图形各两个.
-
(1) 请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
-
(2) 请画出△ABC绕点A顺时针方向旋转90度的⊿A″B″C″;
-
(3) 写出B″的坐标,点B关于原点对称点B1的坐标.


-
(1) 画出△ABC绕点B逆时针旋转90°后得到的△A1BC1 , 其中A、C分别和A1、C1对应.
-
(2) 平移△ABC,使得A点落在x轴上,B点落在y轴上,画出平移后的△A2B2C2 , 其中A、B、C分别和A2B2C2对应.
-
(3) 填空:在(2)的条件下,设△ABC,△A2B2C2的外接圆的圆心分别为M、M2 , 则MM2=.

①建立适当的平面直角坐标系,写出各个顶点的坐标;
②将△ABC向左平移5个单位,请在图中画出平移后的△A1B1C1;
③将△A1B1C1绕点C1按逆时针旋转90°,请在图中画出旋转后的△A2B2C1.

-
(1) 画出△ABC关于原点O的中心对称图形DA1B1C1 , 并写出点A1的坐标;
-
(2) 将△ABC绕点C顺时针旋转90°得到DA2B2C,画出DA2B2C,求在旋转过程中,线段CA所扫过的面积.
 中,
中,  ,延长
,延长  使
使  ,线段
,线段 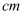 绕点C顺时针旋转90°得到线段
绕点C顺时针旋转90°得到线段  ,连结
,连结  .
. 
-
(1) 依据题意补全图形;
-
(2) 当
 时,
时,  的度数是;
的度数是;
-
(3) 小聪通过画图、测量发现,当
 是一定度数时,
是一定度数时,  .
. 小聪把这个猜想和同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:通过观察图形可以发现,如果把梯形
 补全成为正方形
补全成为正方形  ,就易证
,就易证  ,因此易得当
,因此易得当  是特殊值时,问题得证;
是特殊值时,问题得证;想法2:要证
 ,通过第(2)问,可知只需要证明
,通过第(2)问,可知只需要证明  是等边三角形,通过构造平行四边形
是等边三角形,通过构造平行四边形  ,易证
,易证  ,通过
,通过  ,易证
,易证  ,从而解决问题;
,从而解决问题;想法3:通过
 ,连结
,连结  ,易证
,易证  ,易得
,易得  是等腰三角形,因此当
是等腰三角形,因此当  是特殊值时,问题得证.
是特殊值时,问题得证.请你参考上面的想法,帮助小聪证明当
 是一定度数时,
是一定度数时,  .(一种方法即可)
.(一种方法即可)

-
(1) 在图①中确定格点D,并画出以A.B.C.D为顶点的四边形,使这个四边形为轴对称图形.(画一个即可)
-
(2) 在图②中确定格点E,并画出以A.B.C.D为顶点的四边形,使这个四边形为中心对称图形.(画一个即可)

-
(1) 画出△ABC关于y轴的对称图形△A1B1C1;
-
(2) 将△ABC绕点O顺时针旋转90°得到△A2B2C2 , 请在网格中画出△A2B2C2 , 并直接写出线段B1B2的长.

-
(1) ①将△ABC向右平移4个单位得△A1B1C1 , 画出△A1B1C1;
②画出△A1B1C1关于原点对称的△A2B2C2;
-
(2) 由△ABC和△A2B2C2组成的图形是中心对称图形吗?如果是,请直接写出对称中心的坐标.
 的正方形网格中,两条网格线的交点叫做格点,每个小正方形的边长均为1.以点
的正方形网格中,两条网格线的交点叫做格点,每个小正方形的边长均为1.以点  为圆心,5为半径画圆,共经过图中个格点(包括图中网格边界上的点).
为圆心,5为半径画圆,共经过图中个格点(包括图中网格边界上的点). 
 的位置如图所示:(每个方格都是边长为1个单位长度的正方形,
的位置如图所示:(每个方格都是边长为1个单位长度的正方形,  的顶点都在格点上).
的顶点都在格点上). 
-
(1) 画出
 关于
关于  轴对称的
轴对称的  ;写出
;写出  点对应点
点对应点 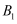 的坐标;
的坐标;
-
(2) 将
 绕点
绕点  逆时针旋转
逆时针旋转  得到
得到  ,请你求出线段
,请你求出线段  旋转过程中扫过的面积.
旋转过程中扫过的面积.

⑴请画出△ABC关于点O的对称图形△A1B1C1;
⑵将△ABC绕原点O逆时针旋转90°后得到△A2B2C2 , 请画出△A2B2C2并求出在旋转过程中点B所经过的圆弧长.

-
(1) 画出将△ABC向左平移4个单位后得到的△A1B1C1 , 并写出点A1的坐标;
-
(2) 画出把△ABC绕原点O旋转180°后得到的△A2B2C2 , 并写出点A2的坐标;
-
(3) 观察图形可知,△A1B1C1与△A2B2C2关于点( )中心对称.

-
(1) 在网格中画出△A1B1C1和△A2B2C1;
-
(2) 计算线段A1C1在变换到A2C1的过程中扫过区域的面积.
- 下图表示叶片的光合作用强度与植物周围空气中的CO2浓度的关系,ce段是增大了光照强度后测得的曲线。下列有关叙述错误的是:
- 华夏族是汉族的前身,是中华民族的主干部分,为华夏族的形成作出最重要贡献的两位部落联盟的首领是() A.黄帝和尧
- 如图,在中,是斜边上两点,且将绕点顺时针旋转90°后,得到连接下列结论:① ② ③的面积等于四边形的面积;④ ⑤其中正确
- 为庆祝中国成立91周年,某学校准备举行“光辉的足迹”图片展。下列四幅图片按时间先后排序正确的是①开天辟地 ②
- 图7所示正确的是
- 胰岛分泌的调节是一个复杂的过程,下图为胰液分泌调节的示意图(部分)。请据图回答:(1)人体在正常情况下,咀嚼食物引起胰液
- 已知单位圆有一条长为的弦,动点在圆内,则使得的概率为( ) A. B. C.
- 为了响应国家“节能减排”的号召,同学们讨论家用汽车的节能方法,你认为下列方法不合理的是() A.开车过程中不宜频繁的急加
- 以保护环境和垃圾资源化为目的,将城市生活垃圾进行分类,下列属于同一类的 是() A.玻璃瓶、塑料袋
- 阅读下面这首宋诗,完成下面小题。 红 梅① 苏 轼 怕愁贪睡独开迟,自恐冰容不入时。故作小红桃杏色,尚余孤瘦雪霜姿。
- 某工厂开发研制了一种高、中、低三档家用电火锅,观察其内部结构发现是由两个相同的发热电阻丝构成.改变档位就是改变电热丝连入
- 17.补写出下列名句名篇中的空缺部分。 ⑴骐骥一跃,不能十步, ,功在不舍。 (荀子《劝学》)
- (2010鸡西)用如图所示的装置,匀速向上提起重2N的物体,所用的拉力为1.5N,动滑轮的机械效率为 。如果要
- 四、阅读理解(共40分) A Linda Eva
- 忆江南 【唐】白居易 江南忆,最忆是杭州。山寺月中寻桂子,郡亭枕上看潮头。何日更重游? 1.作者最难忘的是什么季节的
- 雌果蝇体细胞中有8条染色体,在有丝分裂后期细胞中染色体、染 单体和DNA分子数目分别是A.8、16、16
- 新经济政策与战时共产主义政策在农业方面的共同点是() A.国家享有优先获得农民部分农产品的权利 B.农民自由支配交国家后
- 设函数y=f(x)是定义在(0,+∞)上的减函数,并且满足f(xy)=f(x)+f(y),f=1. (1)求f(9)的值
- It’s a bad practice to ____ children much money as a New Yea
- 下列有关金属的说法正确的是 ( )A.铝具有很好的抗腐蚀性能B.铜能置换出酸中的氢C.钢是纯净物D.银能把铁



