初中 数学
 D .
D . 
 =。
=。 ,则斜坡AB的长是米.
,则斜坡AB的长是米. 

 的说法,错误的是( )
的说法,错误的是( )
 随
随  的增大而减小
C . 图象与
的增大而减小
C . 图象与  轴交于点
轴交于点  D . 当
D . 当  时,
时, 
 、
、  、
、  、
、  中,最简分式的个数是个.
中,最简分式的个数是个.
 的长为2,
的长为2,  为
为  上一个动点,分别以
上一个动点,分别以  、
、  为斜边在
为斜边在  的同侧作两个等腰直角三角形
的同侧作两个等腰直角三角形  和
和  ,那么
,那么  长的最小值是.
长的最小值是.

 =±3
D .
=±3
D . 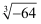 =
= 
 在第二象限,则
在第二象限,则 的可能取值为( )
的可能取值为( )
 B .
B .  C . 4
D .
C . 4
D . 
-
(1) 证明:不论m为何值时,方程总有实数根;
-
(2) 当m为何整数时,方程有两个不相等的整数根.
 的解是()
的解是()
 B .
B .  C .
C .  D .
D . 
| 成绩/分 | 84 | 88 | 92 | 96 | 100 |
| 人数/人 | 2 | 4 | 9 | 10 | 5 |
某校为了开展“阳光体育运动”,计划购买篮球和足球,已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.
(1)每个篮球、每个足球的价格分别为多少元?
(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?
用小立方块搭成一个几何体,使它的主视图和俯视图如图所示。如果n表示小立方块的总块数,n的取值为
![]()


主视图 ![]() 俯视图
俯视图
如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第20个图需要黑色棋子的个数为_________.

猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中 ,
两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
| 类别 价格 | | |
| 进货价(元 / 个) | | |
| 销售价(元 / 个) | | |
( 1 )第一次小李用 
,
两款玩偶共

( 2 )第二次小李进货时,网店规定 款玩偶进货数量不得超过
款玩偶进货数量的一半.小李计划购进两款玩偶共

( 3 )小李第二次进货时采取了( 2 )中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小李来说哪一次更合算?
(注:利润率 
- 世界上海洋和陆地的比例是( ) A.四分之一是海洋 B.三分之二是陆地C.三分陆地
- 用所学的化学知识解答下列问题。 (1) 物质是由分子、 和 构成的。如氧气是由大量的
- .Jessica has to do the job she doesn’t like. She is sufferin
- 山东省所在的地理区域是( ) A.北方地区 B.南方地区 C.西北地区 D
- 下列词语中加点的字,读音完全正确的一组是( ) A、咎言(jiù) 城隅(yú) 葳蕤(ruí) 隰
- 已知,则 。
- 对于天地万物的形成和人类的起源,历史上有过各种各样的神创说。但在历史上,也有许多思想家不断地对神创说进行批驳。科学每发展
- Mr Smith, of the speech, started to read a novel.
- 下列有关细胞的说法中错误的是( ) A.所有的生物都是由细胞构成的 B.细胞是生物体的结构单位,也是生物体的功能单位
- 补写出下列名篇名句中的空缺部分。 古代文人善于把抽象的感觉形象化,如李煜《虞美人》中的“问君能有几多愁? ”
- 经实验测得衣藻DNA在细胞中分布如下:84%在染色体上,14%在叶绿体上,1%在线粒体上,1%游离于细胞质中。这些数据说
- 现有银、铜、铁三种金属,某研究小组的同学为探究银、铜、铁的金属活动性顺序,设计了三个实验:I.将铁片浸入稀硫酸中;II.
- 已知函数 (1)当时,求函数的最大值和最小值; (2)求实数的取值范围,使在区间上是单调函数
- 现代文阅读(9分,每小题3分) 阅读下面的文字,完成第l—3题。 网络文学:什么才是人们该关注的 潘凯雄
- 氢氧化铁胶体稳定存在的主要原因是 ( ) A.胶粒直径小于1n
- .高等植物细胞和动物细胞之间,在细胞分裂的机制上的不同点是:( ) ① 着丝点分裂 ② 细胞质分裂 ③ 纺锤丝的功
- 世界上跨纬度最广、陆地面积最大的大洲是( ) A.亚洲 B.北美洲 C.非洲
- 在世界现代化进程中,各国发展模式不尽相同。 请回答: (1)以美国和苏联为例,说明“自由放任”模式和“计划经济”模式产生
- The millionaire passed away, leaving his children with a lar
- 已知与成正比例,且时,.1.(1)求与的函数关系式;2.(2)当时,求的值;3.(3)将所得函数图象平移,使它过点(2,





