初中 数学
如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是

如图,直线AB与CD相交于点E,∠BEC=45°,射线EG在∠AEC内(如图1),

-
(1) 若∠CEG比∠AEG小25°,求∠BEG的大小;
-
(2) 若射线EF平分∠AED,∠FEG=m°(m>90)(如图2),则∠AEG-∠CEG=(用含m的代数式表示,请直接写出结果).
小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图. 请根据图中信息,解答下列问题:

-
(1) 这次被调查的总人数是多少?
-
(2) 试求表示A组的扇形圆心角的度数,并补全条形统计图;
-
(3) 如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.
如图,在  中,
中,  ,
,  ,
,  ,点D是边
,点D是边  上的动点,过点D作
上的动点,过点D作  于E点.请探究下列问题:(1)若
于E点.请探究下列问题:(1)若 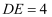 ,则
,则  ;(2)若
;(2)若  ,设点F是边
,设点F是边  上的动点,连接
上的动点,连接  、
、 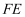 ,以
,以  、
、 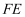 为邻边作平行四边形
为邻边作平行四边形  ,且使得顶点G恰好落在
,且使得顶点G恰好落在  边上,则
边上,则  .
.
 中,
中,  ,
,  ,
,  ,点D是边
,点D是边  上的动点,过点D作
上的动点,过点D作  于E点.请探究下列问题:(1)若
于E点.请探究下列问题:(1)若 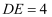 ,则
,则  ;(2)若
;(2)若  ,设点F是边
,设点F是边  上的动点,连接
上的动点,连接  、
、 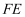 ,以
,以  、
、 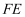 为邻边作平行四边形
为邻边作平行四边形  ,且使得顶点G恰好落在
,且使得顶点G恰好落在  边上,则
边上,则  .
. 
已知在  中,
中, 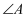 、
、 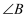 都是锐角,且
都是锐角,且  ,
,  ,那么
,那么  度.
度.
 中,
中, 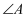 、
、 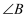 都是锐角,且
都是锐角,且  ,
,  ,那么
,那么  度.
度.
国家环保局统一规定,空气质量分为5级.当空气污染指数达0﹣50时为1级,质量为优;51﹣100时为2级,质量为良;101﹣200时为3级,轻度污染;201﹣300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如图两幅不完整的统计图.请根据图中信息,解答下列各题:

-
(1) 本次调查共抽取了天的空气质量检测结果进行统计;
-
(2) 补全条形统计图;
-
(3) 扇形统计图中3级空气质量所对应的圆心角为°;
-
(4) 如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
已知 , 则下列四个不等式中,不正确的是( )
, 则下列四个不等式中,不正确的是( )
 , 则下列四个不等式中,不正确的是( )
, 则下列四个不等式中,不正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
﹣a的相反数是.﹣a的相反数是﹣5,则a=.
 的相反数是;绝对值不大于4的整数有.
的相反数是;绝对值不大于4的整数有.
如图,在 中,点D,E分别是
中,点D,E分别是 的中点,
的中点, 与
与 相交于点F.若
相交于点F.若 , 则
, 则 的长是.
的长是.
 中,点D,E分别是
中,点D,E分别是 的中点,
的中点, 与
与 相交于点F.若
相交于点F.若 , 则
, 则 的长是.
的长是.
如图,抛物线y=ax2+bx+c和直线y=kx+b都经过点(﹣1,0),抛物线的对称轴为x=1,那么下列说法正确的是( )

A . ac>0
B . b2﹣4ac<0
C . k=2a+c
D . x=4是ax2+(b﹣k)x+c<b的解
如图所示,该几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .
如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.

-
(1) 在图1中画出以AB为底边的等腰直角△ABC , 点C在小正方形顶点上,且△ABC的面积为5
-
(2) 在图2中画出以AB为一腰的等腰三角形ABD , 点D在小正方形顶点上,且△ABD的面积为6
-
(3) 在(2)的条件下,请直接写出△ABD的周长.
当代数式 的值等于7时,代数式
的值等于7时,代数式 的值是.
的值是.
 的值等于7时,代数式
的值等于7时,代数式 的值是.
的值是.
(列二元一次方程组求解)小明家离学校2km,其中有一段为上坡路,另一段为下坡路.他从家跑步去学校共用了16min,已知小明在上坡路上的平均速度是4.8km/h,在下坡路上的平均速度是12km/h.求小明上坡、下坡各用了多少min?
已知方程x2+kx-6=0的一个根是2,则它的另一个根为( )
A . 1
B . -2
C . 3
D . -3
计算:|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |+…+|
|+…+|![]() ﹣
﹣![]() |
|
如图,直线 
,则
的度数为 _________ .

利用三角形的中线,你能否将图中的三角形的面积分成相等的四部分?(给出3种方法)

若4a+9与3a+5互为相反数,则a的值为_____.
最近更新
- 甲、乙两同学进行课外实验,各取250 mL无色透明饮料瓶一个,依次加入4 g氢氧化钠、4 g葡萄糖、半瓶水、3滴0.2%
- 英王詹姆士一世明确提出“君权神授”,其根本目的是 A、从神学角度论证君主专制的合理性 B、为推行君主专制统治制造依据
- 如图所示的装置,C、D、E、F、X、Y都是惰性电极。将电源接通后,向乙中滴入酚酞溶液,在F极附近显红色。则以下说法不正确
- 36.Surveys demonstrate that a majority of urban residents no
- 通常当人走向银行门口时,门就会自动打开,是因为门上安装了下列那种传感器 A.温度传感器 B.压力
- 下列离子方程式书写正确的是 ( ) A.碳酸钙与盐
- 宣传画不仅是艺术,而且还折射出时代风貌。观察下列宣传画,其中反映20世纪50年代末社情的是( )
- 、为了既保护鸟类又保证飞机的飞行安全,机场大多采用“鸟击雷达探测系统”探测机场附近鸟情,利用“驱鸟王”播放同类的哀鸣或天
- 下列关于人体细胞呼吸的叙述,正确的是A.是否产生二氧化碳是有氧呼吸和无氧呼吸的主要区别B.有氧呼吸过程中,中间产物丙酮酸
- 下列性质属于纸张化学性质的是() A.白色 B.不溶于水 C.可燃 D.易撕碎
- 在密闭容器中,对于反应N2+3H22NH3(g),N2、H2起始分别为10mol、30mol,达平衡时H2的转化率为25
- 反应CaCO3CaO+CO2在不同的温度下,在密闭容器中达到平衡的压强如下: 温度/℃550650750850897压强
- 某种用来束缚原子的磁场,其磁感线分布如图所示。以O点(图中白点)为坐标原点,沿Z轴正方向磁感应强度B大小的变化最有可能是
- 在一定温度下,有a.盐酸 b.硫酸 c.醋酸三种酸: (1)当三种酸物质的量浓度相同时,c(H+)由大到小的顺序是
- 分子间同时存在吸引力和排斥力,下列说法正确的是( )A.固体分子间的吸引力总是大于排斥力B.气体能充满任何容器是因
- 为了测定黄铜(铜、锌合金)的组成,某研究性学习小组称取该样品10g,向其中逐滴加9.8的稀硫酸至刚好不再产生气体为止。反
- 优生学是利用遗传学原理改善人类遗传素质,预防遗传病发生的一门科学。以下不属于优生措施的是() A.提倡适龄生育 B
- (浙江省2009届高考押题卷20题)14-16世纪的西欧文学与中国明末清初的文学都体现了反封建、追求个性解放的时代特征。
- 秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍
- . He was lucky in the accident, but his ___________ car is u



