初中数学：七年级　 八年级　 九年级　 中考　

初中数学

已知，如图，O为直线AB上一点，∠DOE＝90°．若∠AOC＝130°，OD平分∠AOC．

（1）求∠BOD的度数；
（2）通过计算说明OE是否平分∠BOC．

有理数a、b在数轴上的表示如图所示，那么（）

A . -b＞a B . -a＜b C . b＞a D . |a|＞|b|

若a²﹣ab=0（b≠0），则 $\text{[math]}$ =（）

A . 0 B .

C . 0或

D . 1或 2

在一条笔直的公路旁依次有 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个村庄，甲、乙两人同时分别从 $\text{[math]}$ 、 $\text{[math]}$ 两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向 $\text{[math]}$ 村，最终到达 $\text{[math]}$ 村.设甲、乙两人到 $\text{[math]}$ 村的距离 $\text{[math]}$ ， $\text{[math]}$ 与行驶时间 $\text{[math]}$ 之间的函数关系如图所示，请回答下列问题：

（1） $\text{[math]}$ 、 $\text{[math]}$ 两村间的距离为 $\text{[math]}$ ， $\text{[math]}$ ；
（2）求出甲、乙两人到 $\text{[math]}$ 村的距离 $\text{[math]}$ ， $\text{[math]}$ 与行驶时间 $\text{[math]}$ 之间的函数关系式，并求出图中点 $\text{[math]}$ 的坐标；
（3）乙在行驶过程中，何时距甲 $\text{[math]}$ ？

如图，已知：D，E分别是△ABC的边BC和边AC的中点，连接DE，AD，若S_△_ABC=24cm² ，则△DEC的面积的面积为（　　）

A . 4cm² B . 6cm2 C . 8cm2 D . 10cm2

根据下图所示的程序计算y的值，若输入的x值为－3，则输出的结果为( ) ．

A . 5　 B . 1　 C . －5　 D . －1

第19届亚运会将于2022年9月在浙江杭州举行，为了让更多的同学了解亚运会，某校甲、乙两个班级开展“亚运会知识竞答”活动.现将各班竞答成绩分为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 四组，依次对应优秀、良好、中等、合格四个等级，分别赋分为：10分，8分，6分，4分，并制作如下频数分布表和扇形统计图.已知乙班参赛人数为40人.

甲班知识竞答成绩频数分布表

组别	频数（人）
$\text{[math]}$	4
$\text{[math]}$	15
$\text{[math]}$	6
$\text{[math]}$	5

乙班知识竞答成绩扇形统计图

（1）请分别求出甲、乙两个班级竞答成绩的平均分.
（2）根据平均数、中位数、众数及成绩等级分析，你认为哪个班级成绩较好？请简述理由.

在学习图案与设计这一节课时，老师要求同学们利用图形变化设计图案，下列设计的图案中是中心对称图形但是不是轴对称图形的是（）

A .

图片_x0020_100001

B .

图片_x0020_100002

C .

图片_x0020_100003

D .

图片_x0020_100004

如图，△ABC内接于⊙O ， AB为⊙O的直径，过点A作⊙O的切线交BC的延长线于点E ，在弦BC上取一点F ，使AF＝AE ，连接AF并延长交⊙O于点D ．

（1）求证：∠B＝∠CAD；
（2）若CE＝2，∠B＝30°，求AD的长．

一个长为2，宽为1的长方形以下面的四种“姿态”从直线l的左侧水平平移至右侧(下图中的虚线都是水平线).其中，所需平移的距离最短的是（）

A .

B .

C .

D .

如图，在平面直角坐标系中，一次函数的图象经过点 $\text{[math]}$ ，且与正比例函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ，与x轴相交于点 $\text{[math]}$

（1）求m的值及一次函数的表达式.
（2）求△BOC的面积.

阅读材料：若m²－2mn＋2n²－8n＋16＝0，求m、n的值．

解：∵m²－2mn＋2n²－8n＋16＝0，∴(m²－2mn＋n²)＋（n²－8n＋16)＝0

∴（m－n）²＋（n－4）²＝0，∴（m－n）²＝0，（n－4）²＝0，∴n＝4，m＝4．

根据你的观察，探究下面的问题：

（1）已知x²＋2xy＋2y²＋2y＋1＝0，求2x＋y的值；
（2）已知a－b＝4，ab＋c²－6c＋13＝0，求a＋b＋c的值．

为调查本校学生对“关灯一小时”有关情况的了解程度，学校政教处随机抽取部分同学进行了调查，将调查结果分为：“A—不太了解、B—基本了解、C—了解较多、D—非常了解”四个等级，依据相关数据绘制成如下两幅统计图.

（1）这次调查抽取了多少名学生？
（2）根据两个统计图提供的信息，补全这两个统计图；
（3）若该校有3000名学生，请你估计全校对“关灯一小时”非常了解的学生有多少名？

有两个一元二次方程M：ax²+bx+c=0；N：cx²+bx+a=0，其中a•c≠0，a≠c．下列四个结论中，错误的是（　　）

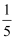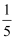A . 如果方程M有两个相等的实数根，那么方程N也有两个相等的实数根 B . 如果方程M的两根符号相同，那么方程N的两根符号也相同 C . 如果5是方程M的一个根，那么 $\text{[math]}$ 是方程N的一个根 D . 如果方程M和方程N有一个相同的根，那么这个根必是x=1

甲、乙两人相约周末登花果山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：

（1）甲登山上升的速度是每分钟米，乙在A地时距地面的高度b为米；
（2）若乙提速后，乙的登山上升速度是甲登山上升速度的3倍，请求出乙登山全程中，距地面的高度y（米）与登山时间x（分）之间的函数关系式（写出自变量范围）；
（3）登山多长时间时，甲、乙两人距地面的高度差为70米？

一个梯形，上底为3 cm，下底为5 cm，高为h cm,则它的面积是_______cm².

方程的根是．

方程的解是

A． B． C． D．

已知：an＝（n＝1，2，3，…），记b1＝2(1－a1)，b2＝2(1－a1)(1－a2)，…，

bn＝2(1－a1)(1－a2)…(1－an)，则通过计算推测出bn 的表达式bn＝ .

（用含n的代数式表示）.

如图7，用直尺和圆规作一个角等于已知角的示意图如图所示，则说明的依据是．

A、SSS B、SAS C、ASA D、AAS

最近更新

　