初中 数学
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为-1和0,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2019次后,数轴上数2019所对应的点是( )

A . 点A
B . 点B
C . 点C
D . 点D
如图,  三个顶点的坐标分别为
三个顶点的坐标分别为  ,
,  ,
,  .
.
 三个顶点的坐标分别为
三个顶点的坐标分别为  ,
,  ,
,  .
. 
-
(1) 请画出
 关于
关于  轴对称的
轴对称的 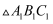 ,并写出点
,并写出点  的坐标;
的坐标;
-
(2) 请画出
 绕点
绕点  逆时针旋转90°后的
逆时针旋转90°后的  ;
;
-
(3) 求出(2)中
 点旋转到
点旋转到  点所经过的路径长(结果保留
点所经过的路径长(结果保留  ).
).
已知a表示一个四位数,b表示一个两位数,把a放到b的左边组成一个六位数,则这个六位数可以表示为.
某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
|
组别 |
正确字数x |
人数 |
|
A |
0≤x<8 |
10 |
|
B |
8≤x<16 |
15 |
|
C |
16≤x<24 |
25 |
|
D |
24≤x<32 |
m |
|
E |
32≤x<40 |
20 |

根据以上信息解决下列问题:
-
(1) 在统计表中,m=,n=,并补全直方图;
-
(2) 扇形统计图中“C组”所对应的圆心角的度数是度;
-
(3) 若该校共有964名学生,如果听写正确的个数少于24个定为不合格,请你估算这所学校本次比赛听写不合格的学生人数.
25的平方根是( )
A . 5
B . -5
C . ± D . ±5
D . ±5
 D . ±5
D . ±5
关于x的方程  =2+
=2+  无解,则m的值为( )
无解,则m的值为( )
 =2+
=2+  无解,则m的值为( )
无解,则m的值为( )
A . -5
B . -8
C . -2
D . 5
某中学初二年级抽取部分学生进行跳绳测试.并规定:每分钟跳90次以下的为不及格;每分钟跳90∼99次的为及格;每分钟跳100∼109次的为中等;每分钟跳110∼119次的为良好;每分钟跳120次及以上的为优秀.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

-
(1) 参加这次跳绳测试的共有人;
-
(2) 补全条形统计图;
-
(3) 在扇形统计图中,“中等”部分所对应的圆心角的度数是;
-
(4) 如果该校初二年级的总人数是450人,根据此统计数据,请你估算该校初二年级跳绳成绩为“优秀”的人数.
如图所示,BD、AC相交于点O,若OA=OD,用“SAS”证明△AOB  △DOC,还需.
△DOC,还需.
 △DOC,还需.
△DOC,还需. 
分式方程 +
+ =
= 的解是 ( )
的解是 ( )
 +
+ =
= 的解是 ( )
的解是 ( )
A . 无解
B . x=2
C . x=-1
D . x=±3
计算
-
(1)

-
(2) 3
 ﹣|
﹣|  |
|
如图,已知CD为⊙O的直径,弦AB⊥CD,垂足为E,连接AD、AC,点F在DC延长线上,连接AF,且∠FAC=∠CAB.
(1)求证:AF为⊙O的切线;
(2)若AD=10,sin∠FAC=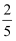 , 求AB的长.
, 求AB的长.

一元二次方程x2+2x+2=0的根的判别式的值为.
若  ,
,  ,则
,则  的值是.
的值是.
 ,
,  ,则
,则  的值是.
的值是.
如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=40°,则∠2等于( )

A . 40°
B . 60°
C . 50°
D . 70°
解下列方程:
-
(1) x2+2x-3=0
-
(2) 3x2-2=5x
下列各曲线中不能表示y是x的函数是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,在∆ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm 的速度移动,点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,∆BPQ的面积。

如图,抛物线y=-x2+(m+2)x+![]() 与x轴交于A(-2-n,0),B(4+n,0)两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A(-2-n,0),B(4+n,0)两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)求此抛物线的解析式;
(2)以点B为直角顶点作直角三角形BCE,斜边CE与抛物线交于点P,且CP=EP,求点P的坐标;
(3)将△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转的角度为α,旋转后的图形为△BO′C ′.当旋转后的△BO′C ′ 有一边与BD重合时,求△BO′C ′ 不在BD上的顶点的坐标.
 |
在![]() 中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点O。某学生在研究这一问题时,发现了如下的事实:
中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点O。某学生在研究这一问题时,发现了如下的事实:
(1)当![]() 时,有
时,有![]() (如图1);
(如图1);
(2)当![]() 时,有
时,有![]() (如图2);
(如图2);
(3)当![]() 时,有
时,有![]() (如图3);
(如图3);

在图4中,当![]() 时,参照上述研究结论,请你猜想用n表示
时,参照上述研究结论,请你猜想用n表示![]() 的一般结论,并给出证明(其中n是正整数)
的一般结论,并给出证明(其中n是正整数)

在数轴上,表示-7的点在原点的 ________侧.
最近更新
- 依次填入下列各句横线上的词语,最恰当的一项是 (1)婴儿只能 到他的内部要求,外部世界只有同他的需要有关的才是
- 如图所示的电路中,只闭合S2时,L1和L2________连接;闭合S1S3,断开S2时,L1和L2__________
- Last month I went tothe UK for a holiday, I first _____ in
- 如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当时,自变量x的取值范围是()A.
- 我国北方某大城市自1982年以来,人口大幅度增加,下表为该城市各圈人口密度、面积等数据。读表完成11~13题。各圈范围
- , ,此事古难全。(苏轼《水调歌头》)
- 用物质的名称或化学式填写下表:名称 水 硝酸锌 氢氧化铜 化学式 NH4CI C6H12O6
- Which do you preferto use to keep in touch with your friends
- 总质量为M的列车,沿水平直线轨道以v匀速前进,最后一节车厢质量为m,中途脱钩,司机发觉时,已行驶了L的距离,于是立即关闭
- 下列说法正确的是( ) (A) 的倒数是 (B)(C) 的相反数是 (D) 的绝对
- 埃及的农业主要集中分布在( ) A、尼罗河谷地和三角洲 B、地中海沿岸地区 C、苏伊士运河两岸
- 小李大学毕业后想自主创业,咨询税务部门得知:大学生创业可以免征、减征企业所得税。对税务部门这一信息的理解,你认为最恰当的
- 如果一个基因的中部缺失了1个脱氧核苷酸对,不可能的结果是 A.无法合成蛋白质产物
- 如图,是杭州PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )(原创) A、表示汽车尾气排放的圆心
- 材料一:自1998年以来,我国各地房地产价格持续上扬,许多地方的住房价格远远超过了普通百姓的购买力。为了抑制房价,200
- 狗外出时走很远也不会忘记回家的路,这是由于它出去时走不远就撒尿,其目的是: ( ) A.与其他的狗沟通信息 B
- 已知反比例函数的图象经过(1,-2),则____________.
- 阅读下面的唐诗,完成下列各题。 阙题 刘眘虚 道由白云尽,春与青溪长。 时有落花至,远随流水香。 闲门向山路,深柳读书堂
- 29.The attackers were arrested and didn’t know where they __
- Tom__________ a report when I telephoned him yesterday afte



