初中 数学
已知关于x的不等式2x-m>-3的解集如图所示,则m的取值为( )
![]()
A . 2
B . 1
C . 0
D . -1
已知等腰三角形△ABC,BC边上的高恰好等于BC边长的一半,则∠BAC的度数是( )
A . 75°
B . 90°或75°
C . 90°或 75°或15°
D . 75°或15°或60°
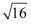 的平方根是( )
的平方根是( )
A . 4
B . -4
C . ±4
D . ±2
计算(﹣2x2y3)•3xy2结果正确的是( )
A . ﹣6x2y6
B . ﹣6x3y5
C . ﹣5x3y5
D . ﹣24x7y5
如图,四边形ABCD是 的内接四边形,其中
的内接四边形,其中 , 则
, 则 的度数为( )
的度数为( )
 的内接四边形,其中
的内接四边形,其中 , 则
, 则 的度数为( )
的度数为( )
A . 130°
B . 100°
C . 80°
D . 50°
一次函数y1=kx-1(k是常数,且k≠0)和y2=x+1图象的交点始终在第三象限,则k的取值范围是.
将方程2x2-4x-3=0配方后所得的方程正确的是( )
A . (2x-1)2=0
B . (2x-1)2=4
C . 2(x-1)2=1
D . 2(x-1)2=5
在函数y=  中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A . x>2
B . x<2
C . x≠2
D . x≥2
下列说法正确的个数为( ).
①若直线  与直线
与直线  相交,则
相交,则  .
.
②若  且a,m都不为0,则直线
且a,m都不为0,则直线  与直线
与直线  平行.
平行.
③若  表示正比例函数,则
表示正比例函数,则  .
.
④若  ,则直线
,则直线  与x轴交于正半轴
与x轴交于正半轴
A . 1
B . 2
C . 3
D . 4
一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“扬”、“州”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
-
(1) 若从中任取一个球,球上的汉字刚好是“扬”的概率为多少?
-
(2) 甲从中任取一球,不放回,再从中任取一球,请用画树状图的方法求出甲取出的两个球上的汉字恰能组成“灵秀”或“扬州”的概率P1;
-
(3) 乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“扬州”的概率为P2 , 指出P1 , P2的大小关系(请直接写出结论,不必证明).
已知等腰三角形的周长为12,底边为y,腰长为x,求y与x的函数关系式,并求自变量x的取值范围
如图,在平面直角坐标系中,已知点A(1,0),将x轴绕点A顺时针旋转60°交y轴于点B,再将点B绕点A顺时针旋转90°得到点C.

-
(1) 求直线BC的解析式;
-
(2) 若点Q为平面直角坐标系中一点,且满足四边形ABCQ为平行四边形,求点Q的坐标;
-
(3) 在直线BC和y轴上,是否分别存在点M和点N,使得以点M,N,A,C为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,说明理由.
已知方程组  中的 x,y互为相反数,则m的值为( )
中的 x,y互为相反数,则m的值为( )
 中的 x,y互为相反数,则m的值为( )
中的 x,y互为相反数,则m的值为( )
A . 2
B . ﹣2
C . 0
D . 4
小颖准备乘出租车到距家超过3km的科技馆参观,出租车的收费标准如下:
| 里程数/km | 收费/元 |
| 3km以内(含3km) | 8.00 |
| 3km以外每增加1km | 1.80 |
则小颖应付车费y(元)与行驶里程数x(km)之间的关系式为.
阅读材料:一般地,对于某个函数,如果自变量x在取值范围内任取x=a与x=  时,函数值相等,那么这个函数是“对称函数”.例如:y=x2 , 在实数范围内任取x=a时,y=a2;当x=
时,函数值相等,那么这个函数是“对称函数”.例如:y=x2 , 在实数范围内任取x=a时,y=a2;当x=  时,y=
时,y=  = a2 ,所以y=x2是“对称函数”.
= a2 ,所以y=x2是“对称函数”.
 时,函数值相等,那么这个函数是“对称函数”.例如:y=x2 , 在实数范围内任取x=a时,y=a2;当x=
时,函数值相等,那么这个函数是“对称函数”.例如:y=x2 , 在实数范围内任取x=a时,y=a2;当x=  时,y=
时,y=  = a2 ,所以y=x2是“对称函数”.
= a2 ,所以y=x2是“对称函数”. 
-
(1) 函数
 ▲ 对称函数(填“是”或“不是”).当x≥0时,
▲ 对称函数(填“是”或“不是”).当x≥0时,  的图象如图1所示,请在图1中画出x<0时,
的图象如图1所示,请在图1中画出x<0时,  的图象.
的图象.
-
(2) 函数
 的图象如图2所示,当它与直线y=-x+n恰有3个交点时,求n的值.
的图象如图2所示,当它与直线y=-x+n恰有3个交点时,求n的值.
-
(3) 如图3,在平面直角坐标系中,矩形ABCD的顶点坐标分别是A(-3,0),B(2,0),C(2,-3),D(-3,-3),当二次函数
 (b>0)的图象与矩形的边恰有4个交点时,求b的取值范围.
(b>0)的图象与矩形的边恰有4个交点时,求b的取值范围.
某种商品原价200元,连续两次降价a%后,售价为148元.下列所列方程正确的是( )
A . 200(1+ a%)2=148
B . 200(1- a%)2=148
C . 200(1- 2a%)=148
D . 200(1-a2%)=148
如图,在平行四边形  中,
中, 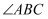 的平分线交
的平分线交  于
于  ,
, 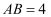 ,
,  ,则
,则  为( )
为( )
 中,
中, 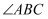 的平分线交
的平分线交  于
于  ,
, 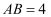 ,
,  ,则
,则  为( )
为( ) 
A . 10
B . 5
C . 3
D . 2
如图,在平面直角坐标系xOy中,一次函数  的图象与反比例函数
的图象与反比例函数  的图象都经过A(
的图象都经过A( 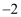 ,
, 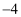 ),B(4,
),B(4,  )两点.
)两点.
 的图象与反比例函数
的图象与反比例函数  的图象都经过A(
的图象都经过A( 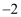 ,
, 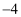 ),B(4,
),B(4,  )两点.
)两点. 
-
(1) 求反比例函数和一次函数的表达式;
-
(2) 过O,A两点的直线与反比例函数图象交于点C,连接BC,求△ABC的面积.
现定义一种新运算:对任意有理数a、b,都有a⊗b=a2﹣b,例如3⊗2=32﹣2=7,2⊗(﹣1)= .
下列化简错误的是………………………………………………………………………( )
(A)![]() ;(B)
;(B)![]() ;(C)
;(C)![]() ;(D)
;(D)![]() .
.
最近更新
- 76. What she said is ________ true. That is to say, not all
- 对于实数、,给出以下三个判断: ①若,则.②若,则 . ③若,则.其中正确的判断的个数是( )A.3
- 德国著名诗人歌德曾对艺术用如下形象的语言进行阐述: 艺术要通过一种完整体向世界说话,但这种完整体不是他(艺术家)在自然界
- 下列两种物质混合后不能发生离子反应的是() A.稀硝酸和碳酸钠溶液混合 B.氯化钠溶液和硝酸银溶液混合 C.硫酸钾溶液和
- 世界博览会已经历150多个春秋,各届博览会都带着深刻的时代烙印。下图所示的体现当时工业成就的展品最有可能出现于 A
- —Tom,please give me some butter. —OK,Mom.________ do you nee
- 下列提高热机的效率的方法中,不可行的是
- —Are you glad that you came to Jilin? — Yes, indeed.I ______
- 全年对太阳能量的利用率,森林生态系统远大于农田生态系统,主要原因是前者 A.以木本植物为主 B.土壤肥沃 C.
- 下列叙述错误的是()A.三大合成材料是指塑料、合成纤维、合成橡胶 B.聚乙烯塑料袋可用加热法封口 C.燃烧法可辨别毛衣的
- .角θ的终边过点P(-1,2),则sinθ等于() A. B. C. -
- 人体中化学元素含量的多少直接影响健康,缺乏下列哪种元素易导致贫血症 A.钙 B.碘
- 句型转换. ⒈He finished his homework yesterday afternoon. (改为否定句)
- 2008年8月8日至8月24日,第二十九届奥运会在我国北京顺利举行。结合有关知识,完成问题。 外国游客在观看体育赛事后,
- 在物质分类中,前者包括后者的是( ) A.氧化物、化合物 B.化合物、酸性氧化物 C.溶液、
- “其书罗列甚远之国,指掌形势,可谓奇书。”“方今急边防,疲氓未息肩。苦心著此书,搜讨颇有年。”这是对下列哪本书的评价?
- 实验是科学探究的重要手段,下列化学实验操作不正确的是
- 在百度贴吧里,一个只有标题“贾君鹏,你妈妈喊你回家吃饭!”没有任何内容的空贴,在短短一天时间内迅速成为网络第一神帖,点击
- 古诗词中有许多关于光的诗句,请你欣赏:“举杯望明月,对影成三人”。这里的三人其中一“人”是由于光的直线传播形成的是___
- 某校一课外活动小组自制一枚火箭,设火箭发射后始终在垂直于地面的方向上运动.火箭点火后可认为做匀加速直线运动,经过4s到达



