初中 数学
探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图像特征,概括函数性质的过程.结合已有的学习经验,请画出函数 的图象并探究该函数的性质.
的图象并探究该函数的性质.
 的图象并探究该函数的性质.
的图象并探究该函数的性质.
|
x |
… |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
… |
|
|
… |
|
a |
|
|
b |
|
|
|
|
… |
|
|
c |
d |
e |
f |
g |

-
(1) 列表,写出表中a,b的值:a= ▲ , b= ▲ ;描点、连线,在所给的平面直角坐标系中画出该函数的图象.
-
(2) 观察函数图象,判断下列关于函数性质的结论是否正确,在下面横线上填入“序号”或填入“无”,正确的是,错误的是.
①函数
 的图象关于y轴对称;
的图象关于y轴对称;②当
 时,函数
时,函数 有最小值,最小值为
有最小值,最小值为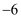 ;
;③在自变量的取值范围内函数y的值随自变量x的增大而减小.
-
(3) 已知二次函数
 , 请你写出表中c,d,e,f,g的值:c= ▲ , d= ▲ , e= ▲ , f= ▲ , g= ▲ , 并在所给的同一坐标系中画出函数
, 请你写出表中c,d,e,f,g的值:c= ▲ , d= ▲ , e= ▲ , f= ▲ , g= ▲ , 并在所给的同一坐标系中画出函数 的图像,结合你所画的函数图象,直接写出不等式
的图像,结合你所画的函数图象,直接写出不等式 的解集.
的解集.
点P(1,﹣5)所在的象限是( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
一个圆柱体和一个圆锥体的底面积相等,它们的体积比是4:3,它们的高度比是。
已知A、B是数轴上任意两点,对应的数分别是a、b , 则表示A、B两点的距离正确的是( )
A . |a|+|b|
B . |a|﹣|b|
C . |a+b|
D . |a﹣b|
某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为。
杭州一月某天的最高气温是  ,最低气温是
,最低气温是  ,那么这天的温差是
,那么这天的温差是  .
.
 ,最低气温是
,最低气温是  ,那么这天的温差是
,那么这天的温差是  .
.
如图,将长方形纸片  沿对角线
沿对角线  折叠,若
折叠,若  ,
,  ,则重叠部分(即
,则重叠部分(即  )的面积是.
)的面积是.
 沿对角线
沿对角线  折叠,若
折叠,若  ,
,  ,则重叠部分(即
,则重叠部分(即  )的面积是.
)的面积是. 
若收入3元记为+3,则支出2元记为( )
A . -2
B . -1
C . 1
D . 2
已知:如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.求证:AB=AD.

如图,已知∠AOB,按照以下步骤画图:
(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M、N为圆心,大于 MN的长半径画弧,两弧在∠AOB内部相交于点C.
MN的长半径画弧,两弧在∠AOB内部相交于点C.
(3)作射线OC.
则判断△OMC≌△ONC的依据是( )

A . SAS
B . SSS
C . ASA
D . AAS
甲乙两人共同计算一道整式乘法题:  .由于甲抄错了第一个多项式中a的符号,得到的结果为
.由于甲抄错了第一个多项式中a的符号,得到的结果为  ;由于乙漏抄了第二个多项式中x的系数,得到的结果为
;由于乙漏抄了第二个多项式中x的系数,得到的结果为  .
.
 .由于甲抄错了第一个多项式中a的符号,得到的结果为
.由于甲抄错了第一个多项式中a的符号,得到的结果为  ;由于乙漏抄了第二个多项式中x的系数,得到的结果为
;由于乙漏抄了第二个多项式中x的系数,得到的结果为  .
.
-
(1) 求正确的a , b的值.
-
(2) 若知道,请计算出这道整式乘法题的符合题意结果.
若规定一种运算:  ,则
,则  .
.
 ,则
,则  .
.
下列命题中,一定是真命题的是( )
A . 同位角相等
B . 三角形中任何两边的和大于第三边
C . 三角分别相等的两个三角形全等
D . 直线 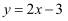 向下平移2个单位可得到一次函数
向下平移2个单位可得到一次函数 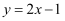 的图象
的图象
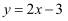 向下平移2个单位可得到一次函数
向下平移2个单位可得到一次函数 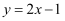 的图象
的图象
-
(1) 计算:

-
(2) 解方程:

计算:
-
(1)
 ;
;
-
(2)
 ;
;
-
(3)
 ;
;
-
(4)
 .
.
建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
-
(1) 若他早上领取备用金4000元,那么下班时应交回银行元钱.
-
(2) 请判断在这七次办理业务中,小张在第次业务办理后手中现金最多,第次业务办理后手中现金最少.
-
(3) 若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
-
(4) 若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.

方程x2-6x+9=0的根的情况是( )
A . 有两个不相等的实数根
B . 有两个相等的实数根
C . 没有实数根
D . 无法判断
单项式  的系数是.
的系数是.
 的系数是.
的系数是.
- 的倒数是;-
的倒数是;- 的平方是.3的相反数是.
的平方是.3的相反数是.
 的倒数是;-
的倒数是;- 的平方是.3的相反数是.
的平方是.3的相反数是.
如图10,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,
∠ABC的角平分线BE交AD于F. 试找出图中所有的等腰三角形,并说明理由.
 |
最近更新
- SARS”病毒的遗传物质中含有核苷酸的种类及碱基的种类分别是( ) A.1、4 B.5、
- 某企业是一家集体企业,由于生产任务较多,未经劳动行政部门批准,要求职工每天加班工作,星期天也照常上班。职工每月累计加班加
- 分析一个DNA分子时,发现30%的脱氧核苷酸含有腺嘌呤,由此可知该分子中一条链上鸟嘌呤含量的最大值可占此链碱基总数的
- 阅读下面的文字,按照要求作文。(60分) 中国自古有“学而知之”的说法,这里的“学”,通常被理解为从师学习。韩愈就说过:
- 下图表示在25℃时,A、B两种植物随着光照强度的变化,吸收量或释放量的变化曲线图。据图回答下列问题:(1)写出光合作用的
- 漳州市被国家交通运输部列为国家公路运输枢纽城市,现拥有营运客货车月21000辆,21000用科学记数法表示为()A 0.
- 能使两个直角三角形全等的条件是( ) A. 两直角边对应相等
- 如图,已知=3e1,=3e2,且C、D是AB的三等分点,则=_____________________,=_______
- 下列关于体温调节的叙述错误的是() A.体温调节中枢在下丘脑 B.体温调节是神经调节和体液调节共同作用的 C.人体的体温
- 2009年,财政部发布了“家电下乡”的政府补贴资金政策,对农民购买手机等四类家电给予销售价格13﹪的财政补贴,以提高农民
- 从2009年2月1日起,财政补贴家电下乡政策推广到全国。财政补贴家电下乡政策 ① 有利于调动农民购买家电积极性,改善农民
- 关于运动员和球类能否看成质点,以下说法正确的是( ) A.研究跳高运动员的起跳和过杆动作时,可以把运动员看成
- Fe元素是地壳中最丰富的元素之一,在金属中仅次于铝,铁及其化合物在生活、生产中有广泛应用。请回答下列问题: (1)磁铁矿
- 将点B(5,-1)向上平移2个单位得到点A(a+b, a-b)。则( )A.a=2, b=3B.a=3, b=
- 6从甲、乙等10个同学中挑选4名参加某项公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有()(A)种 (B)种
- 如图所示,闭合开关S后,A灯与B灯均发光,当滑动变阻器的滑片P向左滑动时,以下说法中正确的是A.A灯变亮
- 某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:尺码(cm)23.52424.52525.5销售量(双)1
- 河南省某市成立行政服务中心,把过去“群众围着政府转”转变为“政府围着群众转”,坚决克服了“门难进、脸难看、话难听、事难办
- 34. We are living in an age ____________ we treasure very mu
- 黄宗羲认为:“秦变封建而为郡县,以郡县得私于我也;汉建庶孽(指诸侯王国),以其可以藩屏于我也;宋解方镇之兵,以方镇之不利











