初中 数学
如图,若△ABC≌△DEF , 且BE=5,CF=2,则BF的长为( )

A . 2
B . 3
C . 1.5
D . 5
三角形有两条边的长度分别是5和7,则最长边a的取值范围是.
如图(1),大正方形的面积可以表示为  ,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即
,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即  .同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:
.同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:  .把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”
.把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”
 ,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即
,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即  .同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:
.同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:  .把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”
.把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法” 
-
(1) 用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个多项式进行因式分解的等式:;

-
(2) 如图(3),
 中,
中,  ,
,  ,
,  ,
,  是斜边
是斜边  边上的高.用上述“面积法”求
边上的高.用上述“面积法”求  的长;
的长; 
-
(3) 如图(4),等腰
 中,
中,  ,点O为底边
,点O为底边  上任意一点,
上任意一点,  ,
,  ,
,  ,垂足分别为点M,N,H,连接
,垂足分别为点M,N,H,连接 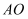 ,用上述“面积法”,求证:
,用上述“面积法”,求证:  .
. 
学期即将结束,为了表彰优秀,班主任王老师用W元钱购买奖品。若以2支钢笔和3本笔记本为一份奖品,则可买60份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品。设钢笔单价为x元/支,笔记本单价为y元/本。
-
(1) 请用y的代数式表示x.
-
(2) 若用这W元钱全部购买笔记本,总共可以买几本?
用一根长为21厘米的铁丝围成一个三条边长均为整数厘米的等腰三角形,则方案的种数为( )
A . 5
B . 6
C . 7
D . 8
计算:

如图,在直角坐标系中,  ,
,  ,
,  ,点D在
,点D在  上,
上,  ,
,  于H.
于H.
 ,
,  ,
,  ,点D在
,点D在  上,
上,  ,
,  于H.
于H. 
-
(1) 判断
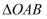 的形状,并说明理由.
的形状,并说明理由.
-
(2) 求点D的坐标.
-
(3) 若P是
 上的动点,当
上的动点,当  的周长最小时,求
的周长最小时,求  的面积.
的面积.
若2是关于x的一元一次方程2x=kx+6的解,则k=
在大课间活动中,体育老师对甲、乙两名同学每人进行10次立定跳远测试,他们的平均成绩相同,方差分别是S甲2=0.20,S乙2=0.16,则甲、乙两名同学成绩更稳定的是
如图,在  中,点
中,点  、
、  分别在
分别在  、
、  上,
上, 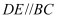 ,点
,点  在
在  的延长线上,
的延长线上,  ,则下列结论错误的是( )
,则下列结论错误的是( )
 中,点
中,点  、
、  分别在
分别在  、
、  上,
上, 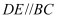 ,点
,点  在
在  的延长线上,
的延长线上,  ,则下列结论错误的是( )
,则下列结论错误的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
把几个数用大括号围起来,中间用逗号断开,如:{1,2,﹣3}、{﹣2,7, ,19},我们称之为集合,其中的数称其为集合的元素,如果一个集合满足:当有理数a是集合的元素时,有理数8﹣a也必是这个集合的元素,这样的集合我们称为好的集合.
,19},我们称之为集合,其中的数称其为集合的元素,如果一个集合满足:当有理数a是集合的元素时,有理数8﹣a也必是这个集合的元素,这样的集合我们称为好的集合.
 ,19},我们称之为集合,其中的数称其为集合的元素,如果一个集合满足:当有理数a是集合的元素时,有理数8﹣a也必是这个集合的元素,这样的集合我们称为好的集合.
,19},我们称之为集合,其中的数称其为集合的元素,如果一个集合满足:当有理数a是集合的元素时,有理数8﹣a也必是这个集合的元素,这样的集合我们称为好的集合.
-
(1) 请你判断集合{3,7},{﹣2,1,4,7,10}是不是好的集合?
-
(2) 请你写出满足条件的两个好的集合的例子.
我们知道:如果点A、B在数轴上分别表示有理数a、b,那么在数轴上A、B两点之间的距离AB=|a-b|.所以式子|x-3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.利用这个结论,请结合数轴解答下列问题:
![]()
-
(1) 数轴上表示0和3的两点之间的距离是;数轴上表示-1和-4的两点之间的距离是;数轴上表示1和-4的两点之间的距离是 .
-
(2) 数轴上表示x和-1的两点之间的距离可以表示为|x-(-1)|,即:|x+1|.
如果|x+1|=2,那么x= .
-
(3) 如果数轴上表示数x的点位于2与-3之间,那么|x-2|+|x+3|的值为 .
-
(4) 当x取时,|x-1|=x+3;当x取时,|x-2|+|x+2|=6.
-
(5) 当x取时,|x+3|+|x-1|+|x-5|的值最小,最小值是
如图,在平面直角坐标系中,  为坐标原点,
为坐标原点, 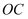 在
在  轴正半轴上,四边形
轴正半轴上,四边形 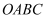 为平行四边形,反比例函数
为平行四边形,反比例函数  的图象经过点
的图象经过点  与边
与边  相交于点
相交于点  ,若
,若  ,
,  ,则
,则  .
.
 为坐标原点,
为坐标原点, 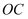 在
在  轴正半轴上,四边形
轴正半轴上,四边形 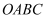 为平行四边形,反比例函数
为平行四边形,反比例函数  的图象经过点
的图象经过点  与边
与边  相交于点
相交于点  ,若
,若  ,
,  ,则
,则  .
.

如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽 时,涵洞顶点与水面的距离是2m.这时,离开水面1.5m处,涵洞的宽DE为( )
时,涵洞顶点与水面的距离是2m.这时,离开水面1.5m处,涵洞的宽DE为( )
 时,涵洞顶点与水面的距离是2m.这时,离开水面1.5m处,涵洞的宽DE为( )
时,涵洞顶点与水面的距离是2m.这时,离开水面1.5m处,涵洞的宽DE为( )
A .  B .
B .  C . 0.4
D . 0.8
C . 0.4
D . 0.8
 B .
B .  C . 0.4
D . 0.8
C . 0.4
D . 0.8
小明从家中出发,到离家1.2千米的早餐店吃早餐,用了一刻钟吃完早餐后,按原路返回到离家1千米的学校上课,在下列图象中,能反映这一过程的大致图象是 ( )
 A. B. C. D.
A. B. C. D.
因式分解:![]() .
.
正比例函数 



因式分解:x2﹣2x= .
方程![]() 的解的相反数是( )
的解的相反数是( )
A.2 B.-2 C.3 D.-3
分解因式:mx-6my =____________
最近更新
- 比较二氧化碳和二氧化硫各一个分子,下列那个数值相等( ) A.含氧分子数 B.含氧的质量分数 C.含氧原子个数
- 22.补写出下列句子中的空缺部分。(每空1分,共6分) (1) 舞幽壑之潜蛟, 。
- 下列交通标志中既是中心对称图形,又是轴对称图形的是() A. B. C. D.
- 下列不是海水淡化主要方法的是( )A. 蒸馏法 B. 离子交换法 C. 电渗析法 D. 干馏法
- 小球从空中由静止下落与水平地面相碰后弹到空中某一高度,其速度一时间图象如图所示,已知重力加速度g=10m/s2,则由图可
- (本小题满分12分) 已知角的终边上有一点P(,m),且m, 求与的值。
- 图3为我国某地典型地貌景观图,读图回答3~4题。3. 此地貌景观最可能位于我国( ) A. 西南地区
- 中国政府对香港和将对澳门恢复行使主权,其原因是( ) A.香港和澳门都是我国领土的一部分 B
- 数字音乐播放器、智能手机和平板电脑等电子产品的问世,改变了人们的生活消费和娱乐方式。这表明 A.消费促进生产
- 据调查,在春节前夕,超市中许多商品的价格有不同程度的上涨。这说明( ) A.供给的变化会引起价格的变化 B.价格
- 中国古代农耕经济重心由北方黄河流域移至南方长江中下游地区的因素是( ) ①中原人口南迁使南方劳动力得到补充②南迁人口使南
- 高考后,一些考生的家长来到寺庙烧香拜佛,希望自己的孩子“取得高分”“金榜题名”。高考考好考坏,关键在考生,在课堂,但绝不
- (2013上海市闸北区期末)如图所示,虚线框内存在一沿水平方向、且与纸面垂直的匀强磁场。现通过图示装置来测量该磁场的磁感
- 若=在上恒正,则实数的取值范围是( )A. B. C. D.
- 2017年5月我国发布了四种新元素的中文名称,如图是其中一种元素的信息,下列有关说法错误的是()A.镆属于金属元素 B.
- 如图所示,固定的半圆弧形光滑轨道置于水平方向的勻强电场和匀强磁场中,轨道圆弧半径为R,磁感应强度为B,方向垂直于纸面向外
- 公元前7世纪后期,导致晋文公成为中原霸主的关键性战争是 A.桂陵之战
- “曹操立不起营寨,心中忧惧……子伯曰:‘连日阴云布合,朔风一起,必大冻矣……’是夜北风大作,操尽驱士兵担土泼水……比及天
- 关于刑事诉讼,下列说法中正确的是( ) ①刑事诉讼以立案为起点②它主要解决人民法院、人民检察院和公安机关在直接受理刑
- 中新网台北2008年11月电:大陆海协会会长陈云林与台湾海基金董事长江丙坤今日在台北举行第二次“陈江会谈”,这将成为两岸



