初中数学：七年级　 八年级　 九年级　 中考　

初中数学

如图，△ABC中，D为BC上一点，∠C＝∠BAD ， △ABC的角平分线BE交AD于点F ．

（1）求证：∠AEF＝∠AFE；
（2） G为BC上一点，当FE平分∠AFG且∠C＝30°时，求∠CGF的度数．

如图1，已知直线y=kx与抛物线y= $\text{[math]}$ 交于点A（3，6）．

（1）求直线y=kx的解析式和线段OA的长度；
（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；
（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？

如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A .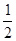

B . 2 C . 10

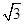D .

已知a，b，c是△ABC的三边长，其中a，b是二元一次方程组 $\text{[math]}$ 的解，那么c的值可能是下面四个数中的（　　）

A . 2 B . 6 C . 10 D . 18

某校随机抽取了50名九年级学生进行立定跳远水平测试，并把测试成绩（单位：m）绘制成不完整的频数分布表和频数分布直方图.

学生立定跳远测试成绩频数分布表

分组	频数
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	12
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	10

请根据图表中所提供的信息，完成下列问题：

（1）表中 $\text{[math]}$ ， $\text{[math]}$ ，样本成绩的中位数落在范围内；
（2）请把频数分布直方图补充完整；
（3）该校九年级组共有1200名学生，请估计该校九年级学生立定跳远成绩在 $\text{[math]}$ 范围内的有多少人？

按照如图所示的计算程序，若输出的结果为13，则输入的正数 $\text{[math]}$ 可以是．

某乡镇对主干道进行绿化，计划把某一段公路的一侧全部栽上合欢树，要求路的两端各栽一棵，中间栽上若干棵，并且相邻两棵树的距离相等。如果每隔5米栽一棵，则树苗缺21棵；如果每隔6米栽1棵，则树苗正好用完。设原有树苗x棵，则根据题意，可得方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

已知关于x的一元二次方程x²﹣（2m+3）x+m²+2=0．

（1）若方程有实数根，求实数m的取值范围；
（2）若方程两实数根分别为x₁、x₂ ，且满足x₁²+x₂²=31+|x₁x₂|，求实数m的值．

下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

AD是△ABC的中线，DE=DF．下列说法：①CE=BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

已知，如图，抛物线y=﹣x²+bx+c经过直线y=﹣x+3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．

（1）求此抛物线的解析式；
（2）若点M为抛物线上一动点，是否存在点M，使△ACM与△ABC的面积相等？若存在，求点M的坐标；若不存在，请说明理由．
（3）在x轴上是否存在点N使△ADN为直角三角形？若存在，确定点N的坐标；若不存在，请说明理由．

已知y与x﹣1成反比例，且当x＝2时，y＝3，求当y＝6时x的值.

已知点P，点A，点B是数轴上的三个点．若点P到原点的距离等于点A，点B到原点距离的和的一半，则称点P为点A和点B的“关联点”．

（1）已知点A表示1，点B表示﹣3，下列各数﹣2，﹣1，0，2在数轴上所对应的点分别是P₁ ， P₂ ， P₃ ， P₄ ，其中是点A和点B的“关联点”的是；
（2）已知点A表示3，点B表示m，点P为点A和点B的“关联点”，且点P到原点的距离为5，求m的值；
（3）已知点A表示a（a＞0），将点A沿数轴正方向移动4个单位长度，得到点B．当点P为点A和点B的“关联点”时，直接写出PB﹣PA的值．

《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马？根据题意，求得大马有匹．

如图，点M在∠AOB的边OB上．

（1）过点M画线段MC⊥AO，垂足是C；
（2）过点C作∠ACF=∠O．（尺规作图，保留作图痕迹）

若a=b，则在①a-3=b-3；② $\text{[math]}$ ；③ $\text{[math]}$ ；④3a-1=3b-1中，正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

如图，AD是△ABC边BC的中线，E、F分别是AD、BE的中点，若△BFD的面积为6，则△ABC的面积等于_____。

方程x（x+1）=2（x+1）的解是　　．

如图，在平面直角坐标系xOy中，点A，B，C满足二次函数的表达式，则对该二次函数的系数和b判断正确的是

A． B．

C． D．

最近更新

　