初中 数学
一次新冠病毒防疫知识竞赛有25道题,评委会决定:答对一道题得4分,答错或不答一题扣1分,在这次知识竞赛中,小明被评为优秀(85分或85分以上),那么小明至少答对了道题.
下列说法正确的是( )
A . 若 a、b、c是△ABC的三边,则a2+b2=c2
B . 若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C . 若 a、b、c是Rt△ABC的三边,  ,则a2+b2=c2
D . 若 a、b、c是Rt△ABC的三边,
,则a2+b2=c2
D . 若 a、b、c是Rt△ABC的三边,  ,则a2+b2=c2
,则a2+b2=c2
 ,则a2+b2=c2
D . 若 a、b、c是Rt△ABC的三边,
,则a2+b2=c2
D . 若 a、b、c是Rt△ABC的三边,  ,则a2+b2=c2
,则a2+b2=c2
已知:x2+y2=5,xy=﹣3,则(x﹣y)2=.
某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数.已知行李质量为20kg时需付行李费2元,行李质量为50kg时需付行李费8元.
-
(1) 当行李的质量x超过规定时,求y与x之间的函数表达式;
-
(2) 求旅客最多可免费携带行李的质量.
不等式的左右两边都是,只含有一个,并且未知数的最高次数是1,像这样的不等式叫做一元一次不等式.
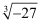 +
+  -
-  =.
=.
利用平方根的定义解方程:2x2-50=0
小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )
A . 三角形
B . 线段
C . 长方形
D . 平行四边形
已知点B在直线AC上,AB=8cm,AC=18cm,P、Q分别是AB、AC的中点,则PQ为cm.
计算:  .
.
 .
.
如图,是一个运算程序的示意图,若开始输入x的值为625,则第2018次输出的结果为.

下列实数中,介于  与
与  之间的是( )
之间的是( )
 与
与  之间的是( )
之间的是( )
A .  B .
B .  C .
C . 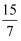 D .
D . 
 B .
B .  C .
C . 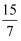 D .
D . 
对于实数x , 我们规定[x]表示不大于x的最大整数,例如[1.4]=1.若[  ]=5,则x的取值范围是( )
]=5,则x的取值范围是( )
 ]=5,则x的取值范围是( )
]=5,则x的取值范围是( )
A . x≥13
B . x≤16
C . 13≤x<16
D . 13<x≤16
如图,在▱ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )

A . 3
B . 6
C . 12
D . 24
如图,在平面直角坐标系中,直线y= 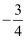 x+15分别交x轴、y轴于点A,B,交直线y=
x+15分别交x轴、y轴于点A,B,交直线y=  x于点M。动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒。
x于点M。动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒。
 x+15分别交x轴、y轴于点A,B,交直线y=
x+15分别交x轴、y轴于点A,B,交直线y=  x于点M。动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒。
x于点M。动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒。 
-
(1) 求点A的坐标和AM的长。
-
(2) 当t=5时,线段CD交OM于点P,且PC=PD,求a的值。
-
(3) 在点C的整个运动过程中,
①直接用含t的代数式表示点C的坐标。
②利用(2)的结论,以C为直角顶点作等腰直角△CDE(点C,D,E按逆时针顺序排列)。当OM与△CDE的一边平行时,求所有满足条件的t的值。
如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD的面积.

《孙子算经》中有一道题,原文是:“今有木,不知长短。引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问木长多少尺?如果设木长  尺,绳子长
尺,绳子长  尺,则下列方程组正确的是( )
尺,则下列方程组正确的是( )
 尺,绳子长
尺,绳子长  尺,则下列方程组正确的是( )
尺,则下列方程组正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,抛物线  与
与  轴交
轴交  、
、  两点(
两点(  点在
点在  点左侧),直线
点左侧),直线  与抛物线交于
与抛物线交于  、
、  两点,其中
两点,其中  点的横坐标为2.
点的横坐标为2.
 与
与  轴交
轴交  、
、  两点(
两点(  点在
点在  点左侧),直线
点左侧),直线  与抛物线交于
与抛物线交于  、
、  两点,其中
两点,其中  点的横坐标为2.
点的横坐标为2. 
-
(1) 求
 、
、  两点的坐标及直线
两点的坐标及直线  的函数表达式;
的函数表达式;
-
(2)
 是线段
是线段  上的一个动点,过
上的一个动点,过  点作
点作  轴的平行线交抛物线于
轴的平行线交抛物线于  点,求线段
点,求线段  长度的最大值;
长度的最大值;
-
(3) 点
 是抛物线上的动点,在
是抛物线上的动点,在  轴上是否存在点
轴上是否存在点  ,使
,使  、
、  、
、  、
、  四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的
四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的  点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.
点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.
.用“>”、“<”、“=”号填空:
﹣0.02 1;
如图,已知两个等圆![]() 和
和![]() 相交于A、B两点,
相交于A、B两点,![]() 经过点
经过点![]() ,点C是
,点C是![]() 上的任一点(不与A、
上的任一点(不与A、![]() 、B重合),连BC,并延长交
、B重合),连BC,并延长交![]() 于D,连结AC、AD,求证:______________________。
于D,连结AC、AD,求证:______________________。
(1)操作、测量:将图按照题中叙述补充完整,并观察或度量AC、CD、AD三条线段的长短,通过观察或度量,说出三条线段之间的关系。
(2)猜想结论(求证部分),并证明你的猜想(在你补充完整的图中证明)。

最近更新
- 某校高一的新同学分别乘两辆汽车去市公园游玩.两辆汽车在平直公路上运动,甲车内一同学看见乙车没有动,而乙车内一同学看见路旁
- ----- ? ----- They’re fine, thank y
- Thearticle gives students some ___________ about how to sta
- 化学用语是最简明、信息丰富、国际通用的语言。请用化学用语填空: 2个金原子 ;
- 下列物质在氧气中燃烧,火星四射,生成黑色固体的是A.木炭 B.镁条 C.红磷
- 112°E 读“我国某区域1月和7月等温线分布图”,回答15—16题。 图例 河流 7月等温线(°C)
- (16分)已知X、Y、Z、T四种元素中,只有T不是短周期元素,与它们有关部分信息如下表: (1)Y元素位于周期表的第
- 根据如图11-17所示实验,判断下列说法错误的是 ()图11-17 A.浓盐酸有挥发性 B.氯化氢分子在运动 C.Y杯溶
- 下列词语中加点的字,读音全都正确的一组是 A.癸丑(guǐ) 女红(gāng) 蕈菌(jūn) 茕茕孑
- 激光散斑测速是一种崭新的测速技术,它应用了光的干涉原理.用二次曝光照相所获得的“散斑对”相当于双缝干涉实验中的双缝,待测
- 装有胶卷的照相机和眼球有很多相似之处,下面各组照相机和眼球对应的结构,功能不相似的是 A.闪光灯和角膜 B.胶卷和视
- 在溶液中能大量共存的一组离子或分子是 A.NH4+ 、H+、NO3-、HCO3- B.K+
- 现代文阅读 奔跑的火焰
- 1. 漂浮在水面上的一块冰熔化成水,保持不变的物理量是 ( )A.体积
- 1978年春修订的《中华人民共和国宪法》规定,“全国人民在新时期的总任务是:坚持无产阶级专政下的继续革命”,同时把原宪法
- 有一种粉末它是由铁的氧化物中的一种或者两种组成,取3.04 g粉末加热,同时通入足量的CO使之完全反应,再用过量澄清石灰
- Our English teacher is very strict _______ us.A.with
- 下列实验、现象及相关结论均正确的是( ) 现象 品红褪色 最后试管有浅黄色沉淀 最后一滴溶液使酚酞由无色变为粉红色,
- 商鞅变法法令规定:“戮力本业,耕织致粟帛多者,复其身。事末利及怠而贫者,举以为收孥”。这项规定不利于A.保护农民阶级的利
- 下图表示培养液中K+浓度及溶氧量对小麦根系吸收K+速率的影响。下列有关两曲线形成机理的解释错误的是( )①曲线ab



