初中 数学
先化简,再求值:  ,其中x是整数且-3﹤x﹤1.
,其中x是整数且-3﹤x﹤1.
 ,其中x是整数且-3﹤x﹤1.
,其中x是整数且-3﹤x﹤1.
如图是由几个相同的小立方体组成的左视图和俯视图,小立方块的个数最少是 .

已知m为整数,方程组  有正整数解,则m=.
有正整数解,则m=.
 有正整数解,则m=.
有正整数解,则m=.
如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )

A . 32°
B . 48°
C . 60°
D . 66°
已知关于x的一元二次方程(a+1)x2+2x+1﹣a2=0有一个根为﹣1,求a的值.
如图①,将△ABC绕点A逆时针旋转90°得到△ADE.

-
(1) DE与BC的位置关系为;
-
(2) 如图②,连接CD,BE,若M为BE的中点,连接AM,请探究线段AM与CD的关系,并给予证明;
-
(3) 如图③,已知E是正方形ABCD的边BC上任意一点,以AE为边作正方形AEFG,连接BG,M为BG的中点,连接AM.
①若AB=4,BE=3,求AM的长;
②若AB=a,BE=b,则AM的长为 ▲ . (用含a,b的代数式表示)
计算 (2x+1)(x﹣1)﹣(x2+x﹣2)的结果,与下列哪一个式子相同?( )
A .  ﹣2x+1
B .
﹣2x+1
B .  ﹣2x﹣3
C .
﹣2x﹣3
C .  +x﹣3
D .
+x﹣3
D .  ﹣3
﹣3
 ﹣2x+1
B .
﹣2x+1
B .  ﹣2x﹣3
C .
﹣2x﹣3
C .  +x﹣3
D .
+x﹣3
D .  ﹣3
﹣3
若关于x的不等式组  恰有3个整数解,则m的取值范围是( )
恰有3个整数解,则m的取值范围是( )
 恰有3个整数解,则m的取值范围是( )
恰有3个整数解,则m的取值范围是( )
A . 4<m<5
B . 4≤m<5
C . 4<m≤5
D . 4≤m≤5
下列每组数分别是三根小木棒的长度,其中能摆成三角形的是( )
A . 3,4,5
B . 7,8,15
C . 3,12,20
D . 5,11,5
已知线段a和线段AB(a<AB).
![]()
-
(1) 以AB为一边,画△ABC,使AC=a,∠A=50°,用直尺、圆规作出△ABC边BC的垂直平分线,分别与边AB、BC交于点D、E,联结CD;(不写画法,保留作图痕迹)
-
(2) 在(1)中,如果AB=5,AC=3,那么△ADC的周长等于.
规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:
①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);
④若点(m,n)在反比例函数y=  的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A . ①②
B . ③④
C . ②③
D . ②④
小明调查了本班每位同学最喜欢的颜色,并绘制了不完整的扇形图1及条形图2(柱的高度从高到低排列).条形图不小心被撕了一块,图2中 “( )”应填的颜色是( )

A . 蓝
B . 粉
C . 黄
D . 红
如果抛物线y=(m+1)x2的最低点是原点,那么实数m的取值范围是
计算:  .
.
 .
.
若一个扇形的圆心角为90°,半径为6,则该扇形的面积为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,  沿
沿  平移至
平移至 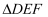 ,
,  ,
,  ,平移距离为6,则阴影部分的面积是.
,平移距离为6,则阴影部分的面积是.
 沿
沿  平移至
平移至 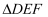 ,
,  ,
,  ,平移距离为6,则阴影部分的面积是.
,平移距离为6,则阴影部分的面积是. 
菱形 的边长为2,
的边长为2, , 点
, 点 、
、 分别是
分别是 、
、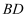 上的动点,
上的动点, 的最小值为.
的最小值为.
 的边长为2,
的边长为2, , 点
, 点 、
、 分别是
分别是 、
、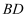 上的动点,
上的动点, 的最小值为.
的最小值为.
在△ABC中,AC=BC,∠ACB=90°,CD⊥AB于D,若S△ABC=16,则CD= .

已知,某一次函数与反比例函数相交于A(1,3),B(m,1),求:
(1)m的值与一次函数的解析式;
(2)△ABO的面积.


![]()
最近更新
- 右图中ACB为晨昏线,C点(经度45°,纬度70°)位于格陵兰岛上。据此完成下面2题。 33.飞机从A地点飞往B
- 甲、乙两球在光滑水平轨道上同向运动,已知它们的动量分别是p甲=5 kg·m/s,p乙=7 kg·m/s,甲追乙并发生碰撞
- 阅读下面的图画材料,根据漫画的寓意,选择一个角度构思作文,题目自拟,文体自定,写一篇不少于800字的作文。
- 在下面的括号里改正错别字( )(2分)(1) 顶礼莫拜( ) (2) 珠乐晶莹 ( )(3) 怒不可谒(
- 若南半球的某风带南侧为高气压带,北侧为低气压带,则该风带盛行风向是 A.东北方 B.东南风
- 在减数分裂中发生,而在有丝分裂中不发生的现象是 A. DNA复制 B. 纺锤体的形 C. 同源染色体分离 D.
- 用H2作还原剂和用金属作还原剂相比,所得金属纯度的说法正确的是A.用H2的高
- 阅读下面文言文,完成下列各题。 马仁瑀,大名夏津人。十余岁时,其父令就学,辄逃归。又遣于乡校习《孝经》,旬余不识一字。博
- 一列简谐横波在某一时刻的波形图如图1所示,图中P、Q两质点的横坐标分别为x=1.5m和x=4.5m。P点的振动图像如图2
- Look! An oldman is crossing the road. Let’s go and help ___
- 下面是权威资料统计,预计世界人口数量的一组数字,请根据表格内容,写一个描写地球 状态的比喻句。(4分)10万年前 300
- A、B、C、D、E、F是常见的六种物质,其中A、B是单质,C、D、E、F均是由两种元素形成的化合物。常温下,A为固体,B
- 读美国本土地理位置示意图,完成下列问题。(10分)(1)美国本土从经度位置看位于 半球,从纬度位置看位于地球五带
- 明朝时,太湖地区出现大量“以机为田,以梭为耒”的家庭;苏州震泽镇及附近镇各村居民“尽逐丝绸之利”;松江地区男女几乎均以棉
- “朝蝇暮蚊”,其主要影响因素是 A、空气 B、温度 C、阳光D、湿度
- 2005年被联合国定为“世界物理年”,以表彰爱因斯坦对科学的贡献.爱因斯坦对物理学的贡献有()A.创立“相对论”
- 重铬酸铵(NH4)2Cr2O7是一种受热易分解的盐,若是发生氧化还原反应而分解,下列各组对重铬酸铵受热分解产物的判断,可
- —Where are the Greens, may I ask? —Well, they ______ to Engl
- 20世纪五六十年代,苏美领导人曾分别谈到:“英国雄师一声吼而天下震撼一切的日子已经一去不复返了。如今,英国已经吓不倒任何
- .下列说法不正确的是 ()。 ①FeCl3溶液可用于铜质印刷线路板制作是因为FeCl3能从含Cu2+的溶液中置换出



