初中 数学

 D . 4
D . 4
-
(1)
 ;
;
-
(2)
 ;
;
-
(3)
 ;
;
-
(4)
 ;
;
-
(5)
 ;
;
-
(6)
 .
.
 的不等式
的不等式  的解集是
的解集是 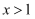 ,则
,则  的取值范围在数轴上表示正确的是( )
的取值范围在数轴上表示正确的是( )

 B .
B .  C .
C .  D .
D . 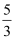
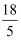 (a> 0)上,则y1, y2, y3的大小关系是( )。
(a> 0)上,则y1, y2, y3的大小关系是( )。
 是完全平方式,则m=.
是完全平方式,则m=.

-
(1)

-
(2)

 B .
B .  C .
C .  D .
D . 
-
(1) a3﹣6a2+5a;
-
(2) (x2+x)2﹣(x+1)2;
-
(3) 4x2﹣16xy+16y2 .

 的方程
的方程  的解是
的解是  ,那么
,那么  的值为.
的值为.

如图, 







A .  B .
B .  C .
C .  D .
D . 
在等式3×(1- )-2×( -1)=15的两个方格中分别填入一个数,使这两个数互为相反数,且等式成立,则第一个方格中的数是 。
解方程组:![]()
两个数相加,如果和为负数,则这两个数( )
A.必定都为负 B.总是一正一负 C.可以都为正 D.至少有一个负数
如图,公园内有一个半径为 18 米的圆形草坪,从 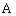
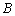


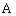
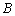


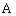
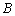

A . 

C . 

- 如图,D是四边形AEBC内一点,连接AD、BD,已知CA=CB,DA=DB,EA=EB. (1)C、D、E三点在一条直线
- 蛇为变温动物,也就是体温随着外界的温度而改变,故推测其较不适合生活于何种生活环境( ) A.热带雨林
- 对下列各句运用的比喻修辞方法分析不恰当的一项是( ) A.明净的兴庆湖犹如一面照妖镜(“照妖镜”这个喻体,人
- 下列动物行为中,属于学习行为的是( ) A.鸡妈妈把小猫掩护在翅膀下 B.蚂蚁觅
- 下列物质最难电离出H+的是( )A.C2H5OH B.H2O C.
- 你校将在假期组织部分学生赴英国学习。作为该项目的负责人,你需负责将两位赴英学生的情况介绍给英方家庭。 [写作内容]
- 宋辽、宋夏和议中的共同内容 A、辽夏向宋称臣
- 血液中的脂质称为血脂,它的主要成分是胆固醇、甘油三酯、磷脂和游离脂肪酸。它们在血液中都与蛋白质结合在一起组成脂蛋白。下图
- 下列关于原子结构、元素性质及元素周期表的结构的说法正确的是 A.元素周期表中位于金属和非金属非界线附近的元素属于过渡元素
- 21.阅读下面的材料,根据要求写一篇不少于800字的文章。 2015年5月2日,中国裸捐第一人余彭年离世。他做过记者,曾
- “五十六个民族,五十六之支花……”,中华五十六个民族大家庭中,哪个民族是元朝时经过长期融合而形成的新民族A.回族B.维吾
- 右图是基因型为AaBb(两对基因独立遗传)的某动物组织切片显微图像,下列说法正确的是 A.细胞分裂先后经过①→③→②过程
- Myparents don’t mind what job I do ________ I am happy. A
- 下图为鸽卵的结构图,请据图回答:(14分)(1)写出图中[2]的名称是 。(2)卵细胞是由[4]
- 已知过氧化氢由过氧化氢和水两种物质组成,实验室常用过氧化氢溶液与二氧化锰混合制取氧气。现将3.6g二氧化锰放入盛有200
- 阅读下面这首古诗,完成(1)(2)两小题。 同儿辈赋未开海棠元好问 枝间新绿一重重,小蕾深藏数点红。 爱惜芳心莫轻吐,且
- 2011年,重庆、上海等城市拟开征房产税。对这一情况,国家有关部门负责人表示,考虑到房产税改革情况复杂,拟先在部分城市对
- 如图,E、B、F、C四点在一条直线上,再添一个条件仍不能证明△ABC≌△DEG的是( )A.AB=DE
- 将一株新鲜的苔藓植物放入其中加有伊红(一种红色染料)的一种浓的盐溶液中,过一定时间后你会看到苔藓的细胞,如下图所示。①,
- 在下列保鲜方法中,依据除去水分防止细菌生长这一原理的措施是 ( ) A.罐藏法保存肉类



