初中 数学
一元二次方程  配方后可变形为( )
配方后可变形为( )
 配方后可变形为( )
配方后可变形为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列运算中,正确的是( )
A . a3÷a2=a
B . a2+a2=a4
C . (ab)3=a4
D . 2ab﹣b=2a
如图,△ABC中,AB=4,∠ACB=75°,∠ABC=45°,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则EF的最小值为。

如图1,已知  ,
,  在
在  内,
内,  在
在 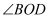 内,
内,  .
.
 ,
,  在
在  内,
内,  在
在 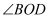 内,
内,  .
. 

-
(1)
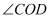 从图1中的位置绕点
从图1中的位置绕点  逆时针旋转到
逆时针旋转到 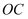 与
与  重合时,如图2,
重合时,如图2, 
 ;
;
-
(2) 若图1中的
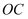 平分
平分  ,则
,则 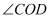 从图1中的位置绕点
从图1中的位置绕点  逆时针旋转到
逆时针旋转到 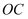 与
与  重合时,旋转了多少度?
重合时,旋转了多少度?
-
(3)
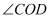 从图2中的位置绕点
从图2中的位置绕点  逆时针旋转
逆时针旋转  ,试问:在旋转过程中
,试问:在旋转过程中 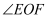 的度数是否改变?若不改变,请求出它的度数;若改变,请说明理由.
的度数是否改变?若不改变,请求出它的度数;若改变,请说明理由.
如图,直线l与⊙O相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF,并分别延长交直线l于B、C两点.

-
(1) 求证:∠ABC+∠ACB=90°;
-
(2) 当⊙O的半径R=5,BD=12时,求tan∠ACB的值.
一项工程,甲队8天完成,乙队要12天完成,甲乙的工作效率的比是
方程  的解与关于x的方程
的解与关于x的方程  的解相同,则
的解相同,则  .
.
 的解与关于x的方程
的解与关于x的方程  的解相同,则
的解相同,则  .
.
如图,已知△ABC三个顶点的坐标分别为A(﹣2,﹣1),B(﹣3,﹣3),C(﹣1,﹣3).将△ABC先向右平移3个单位,再向上平移4个单位得到△A1B1C1 , 在坐标系中画出△A1B1C1 , 并写出△A1B1C1各顶点的坐标.

-
(1) 计算:sin230°+cos245°
-
(2) 解方程:x(x+1)=3
下列运算中正确的是( )
A . b3 •b3 =2b3
B . x 2•x3 =x6
C . (a5 )2 =a7
D . a2 ÷a5 =a-3
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )

A . AB=CD
B . 当AC⊥BD时,它是菱形
C . AB=AC
D . 当∠ABC=90°时,它是矩形
已知﹣2a3by+3与4axb2是同类项,
求代数式:2(x3﹣3y5)+3(3y5﹣x3)+4(x3﹣3y5)﹣2x3的值.
已知 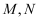 是方程
是方程  的两个实数根,则
的两个实数根,则  .
.
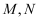 是方程
是方程  的两个实数根,则
的两个实数根,则  .
.
定义新运算符号“*”的运算过程为a*b=  a﹣
a﹣  b,试解方程2*(2*x)=1*x.
b,试解方程2*(2*x)=1*x.
 a﹣
a﹣  b,试解方程2*(2*x)=1*x.
b,试解方程2*(2*x)=1*x.
已知关于x的一元二次方程  有两个不相等的实数根.
有两个不相等的实数根.
 有两个不相等的实数根.
有两个不相等的实数根.
-
(1) 求m的取值范围;
-
(2) 如果m是非负整数,且该方程的根是整数,求m的值.
如图所示,△A′B′C′是△ABC经过平移得到的,![]() △ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标。[来源:学科网ZXXK][来源:Zxxk.Com]
(3)求△A′B′C′的面积。

“华联超市”购进一批20元/千克的绿色食品,如果以30元/千克销售,那么每天可售出400千克。由销售经验知,每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)(
(元)(![]() )存在如右图所示的一次函数关系式。
)存在如右图所示的一次函数关系式。

(1)试求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设“华联超市”销售该绿色食品每天获得利润P元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
在平面直角坐标系中点P![]() 一定在( )
一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象![]() 限.
限.
如图3,在△ABC中,AB=BC,∠A=30°,D是AC的中点,则∠DBC的度数为
A.45° B.50° C.60° D.90°
 |
多项式![]() 的次数是( )
的次数是( )
A.![]() B. C.
B. C.![]() D.
D. ![]()
最近更新
- 用多用表测电阻,调零后用“×10”挡测量一个电阻的阻值,发现表针偏转角度很小,正确的判断和做法是( )A.这个电阻
- 鲁迅在《狂人日记》中写道:“我翻开历史一查,每一页上都写着‘仁义道德’,……仔细看了半夜,才发现满本都写着两个字‘吃人’
- 下图分别是松花江、长江、黄河和西江重要观测站的月平均降水量及河流径流的相对流量(各月径流量占全年径流总量的百分比)分配图
- Our teacher urges us to form a good habit of learning,
- 稀硫酸中插一块铜片,加入下列物质后,可使铜片迅速发生反应的是() A.稀盐酸 B
- 我国某中学地理兴趣小组每天在校园内将12时42分观测到的正午太阳高度记录下来,并根据观测到的数据绘制出当地一年的正午太阳
- 南乡子·冬夜 黄昇 万籁寂无声,衾铁棱棱近五更。香断灯昏吟未稳,凄清。只有霜华伴月明。 应是夜寒凝,恼得梅花睡不成。我念
- 美国人崇尚“今天花明天的钱”的生活和消费方式。不过在金融危机中,“遍体鳞 伤”的金融机构如今再不敢像以往那样随意放贷,转
- 若直线y=x+b与曲线y=3-有公共点,则b的取值范围是 A. B. C.
- 喜爱阅读的同学发现,化学课本中的图表资料可以为我们提供很多信息。 表一:部分酸、碱和盐的溶解性表(20℃)
- 下列物质的性质属于化学性质的是() A.木炭在空气中能燃烧 B.氨气具有剌激性气味 C.二氧化碳的密度比空气大
- 26. With only the fire burning, the room was _____. A. dark
- 已知命题“,使x2+2x +a ≥0”为真命题,则a的取值范围是
- 下列人物中,不属于探索新航路的开拓者的是 A.哥伦布 B.拿破仑
- 如图,磁感强度为B的匀强磁场,垂直穿过平面直角坐标系的第I象限。一质量为m,带电量为q的粒子以速度V从O点沿着与y轴夹角
- 1 .下列各句中加点的词解释不正确的一项是( )A .吾与汝毕力平 险 险:险峻。B . 或 王命急宣 或:有时。C .
- 如图16-7-7,正方形闭合导线框从距磁场区域边界高度为h处自由下落,恰可匀速进入磁场区.若导线框的质量为m、边长为L,
- 设0<α<,0<β<,0<k≤,且sin=k·cosβ,求证:α+β<.
- 谁与我同行 上初中时,学校每周总有二三晚的补习课。家中离学校有三里来路地,白天不觉怎样,,三蹦两跳便到了学校,夜晚
- 为了研究色盲与性别的关系,调查了1000人,调查的结果如下表所示: 男 女 正常 442 514 色盲 38 6 根据上



