初中 数学
已知点A(x1 , y1),B(x2 , y2)在反比例函数  的图象上,若y1<y2<0,则下列结论正确的是( )
的图象上,若y1<y2<0,则下列结论正确的是( )
 的图象上,若y1<y2<0,则下列结论正确的是( )
的图象上,若y1<y2<0,则下列结论正确的是( )
A . x1<x2<0
B . x2<x1<0
C . 0<x1<x2
D . 0<x2<x1
计算2a3•(﹣a5)的结果是( )
A . 2a8
B . ﹣2a8
C . 2a15
D . ﹣2a15
用数学的方式理解“两岸猿声啼不住,轻舟已过万重山”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( )
A . 平移和旋转
B . 对称和旋转
C . 对称和平移
D . 旋转和平移
一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
代数式  有意义,则x的取值可以为( )
有意义,则x的取值可以为( )
 有意义,则x的取值可以为( )
有意义,则x的取值可以为( )
A . -2
B . -1
C . 1
D . 2
把多项式(1+x)(1-x)-(x-1)提取公因式(x-1)后,余下的部分是( )
A . (x+1)
B . -(x+1)
C . x
D . -(x+2)
如图,在正方形网格中,网格线的交点称为格点.已知A,B是两格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则符合题意的点C有( )

A . 6个
B . 7个
C . 8个
D . 9个
解不等式组  ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
在四边形ABCD中,AB∥CD .

-
(1) 如图1,已知∠A=∠B , 求证:AD=BC;
-
(2) 如图2,已知∠A=60°,∠B=45°,AD=2,求BC的长.
如图,建筑物BC上有一旗杆AB,点D到BC的距离为20m,在点D处观察旗杆顶部A的仰角为52°,观察底部B的仰角为45°,则旗杆的高度为m.(精确到0.1m,参考数据: ,
,  ,
,  ,
,  . )
. )
 ,
,  ,
,  ,
,  . )
. )
把下列各数填在相应的集合内:0.25,-|-3|,-  ,-38,10,0.
,-38,10,0.
 ,-38,10,0.
,-38,10,0. 负数集合:{…}
分数集合:{…}
非负整数集合:{…}
元旦期间,大兴商场搞优惠活动,其活动内容是:凡在本商场一次性购买商品超过100元者,超过100元的部分按8折优惠.在此活动中,小明到该商场一次性购买单价为60元的礼盒  (
( 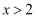 )件,则应付款
)件,则应付款  (元)与商品数
(元)与商品数  (件)之间的关系式,化简后的结果是.
(件)之间的关系式,化简后的结果是.
 (
( 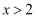 )件,则应付款
)件,则应付款  (元)与商品数
(元)与商品数  (件)之间的关系式,化简后的结果是.
(件)之间的关系式,化简后的结果是.
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )

A . 点C
B . 点D或点E
C . 线段DE(异于端点) 上一点
D . 线段CD(异于端点) 上一点
如图,AD为△ABC的中线,BE为△ABD的中线.

-
(1) ∠ABE=15°,∠BAD=40°,求∠BED的度数;
-
(2) 若△ABC的面积为40,BD=5,则E到BC边的距离为多少.
计算:![]() ;
;![]() ;
;
![]() -
-![]() =1-
=1-![]()
在不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为![]() .
.
(1)试求袋中蓝球的个数.
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.
如图,AB是⊙O的直径,点C,D在⊙O上,OD∥AC,下列结论错误的是
A.∠BOD=∠BAC B.∠BOD=∠COD C.∠BAD=∠CAD D.∠C=∠D
 |
先化简,再求值:![]() ,其中
,其中![]() ,
,![]() .
.
如图,∠AOC=∠BOD,那么∠1 ∠2,理由是 .

最近更新
- (本小题10分)如图,抛物线与x轴交与A(1,0),B(- 3,0)两点,【小题1】(1)求该抛物线的解析式;【小题2】
- 阅读下面的文字,完成1—3题。 对复兴汉服的焦虑 廖保平 最近,汉服运动可谓轰轰烈烈,借汉服以复兴传统文化的声音
- 阅读理解Chris and Jessica live in Miami,Florida. They are packin
- 下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.x 3
- 化学与人体健康密切相关。一些重要的营养素如:糖类、淀粉、油脂、蛋白质、维生素等,对人类的生命活动具有重要意义。作为处在身
- 下列物质中,属于细胞生物膜重要成分的是 A.糖类 B.脂质 C.磷脂
- (山东省平邑一中2009届高三元旦竞赛30题)关于以下二者的说法,错误的是 A.使儒学思想更加理论化、思辩化 B.都认为
- 将石墨置于熔融的钾或气态钾中,石墨会吸收钾而形成称为钾石墨的物质,其组成是C8K、C24K、C36K、C48K和C60K
- 进入青春期,我们的身体在静静变化,我们的心理也发生着一系列的变化。下列心理变化现象中,我们应尽快纠正的是A.思维活跃,想
- 右图为“小鼠皮肤移植实验”过程。相关分析错误的是A.移植皮肤的排斥与细胞免疫有关,与体液免疫无关 B.第二次移植更易发生
- 下列涉及有机物的说法正确的是 ( ) A.苯能与溴单质发生取代反应,
- 干细胞是一种尚未充分分化的未成熟的细胞,它具有再生各种组织、器官的潜能,医学家们正尝试利用干细胞治疗一些顽疾,用骨髓移植
- 下图表示洋葱根尖分生区组织细胞有丝分裂装片的制作与观察过程,据图回答:(1)A过程叫________,作用是______
- —I never drink coffee. —_______ A.So do I B.So did
- 按照从微观到宏观的顺序来描述,动物体的结构层次是() A.细胞→器官→组织→个体 B.细胞→器官→个体 C.细胞→组
- 正确量取15ml液体,应选用的一组仪器是 ( ) ①5ml量筒 ②10ml量筒 ③20ml量筒
- W、X、Y、Z均为短周期主族元素,原子序数依次增加,且原子核外L电子层的电子数分别为0、5、8、8,它们的最外层电子数之
- 你是否曾因为当上班干部成为老师的宠儿无限威风?是否曾因为没当上班干部而深感自卑?最近郑渊洁的一则微博引发了关于班干部制度
- 某同学在进行探究大肠杆菌群体生长规律实验时,正确操作是( ) A.在调整期扩大接种
- 如图所示,杠杆在竖直向下拉力F的作用下将一物体缓慢匀速提升.下表是提升物体时采集到的信息: (1)若不计杠杆自重和摩



