七年级(初一)数学：上学期上册　　 下学期下册

七年级(初一)数学下学期下册试题

如图，△ABC是边长为3的等边三角形，将△ABC沿直线BC向右平移，使点B与点C重合，得到△ECD，连接BE，交AC于F.

图片_x0020_100011

如果 $\text{[math]}$ 是6－x的三次算术根，那么（）

A . x<6 B . x=6 C . x≤6 D . x是任意数

某校七年级实行小组合作学习，为了解学生课堂发言情况，随机抽取该年级部分学生，对他们每天在课堂中发言的次数进行调查和统计，统计表如下，并绘制了两幅不完整的统计图(如图所示).已知A、B两组发言人数直方图高度比为1∶5，请结合图中相关的数据回答下列问题：

已知 $\text{[math]}$ 为第四象限内的点，则一次函数 $\text{[math]}$ 的图象大致是（）

A .

B .

C .

D .

实数 $\text{[math]}$ 的平方根分别是 $\text{[math]}$ 和 $\text{[math]}$ ，且 $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

在抗击新冠疫情期间，市教委组织开展了“停课不停学”的活动.为了解此项活动的开展情况，市教委督导部门准备采用以下调查方式中的一种进行调查：

A.从某所普通中学校随机选取200名学生作为调查对象进行调查；

B.从市内某区的不同学校中随机选取200名学生作为调查对象进行调查；

C.从市教育部门学生学籍档案中随机抽取200名学生作为调查对象进行调查.

（1）在上述调查方式中，你认为比较合理的一个是(填番号).
（2）如图，是按照一种比较合理的调查方式所得到的数据制成的频数分布直方图，在这个调查中，所抽取200名学生每天“停课不停学”的学习时间在1~2小时之间的人数m=.
（3）已知全市共有100万学生，请你利用（2）问中的调查结果，估计全市每天“停课不停学”的学习时间在1~2小时及以上的人数有多少？
（4）你认为这个调查活动的设计有没有不合理的地方？谈谈你的理由.

如图，为某冷饮店一天售出各种口味雪糕数量的扇形统计图，其中售出红豆口味的雪糕200支，那么售出奶油口味雪糕的数量是支．

4月22日是“世界地球日”，学校组织有关知识竞赛，现从中抽取部分学生成绩作为样本，按“优秀”、“良好”、“合格”、“不合格”四个等级进行统计，绘制了如下不完整统计图，

某小区准备新建 60 个停车位，以解决小区停车难的问题。已知新建 $\text{[math]}$ 个地上停车位和 $\text{[math]}$ 个地下停车位共需 1.7 万元：新建 4 个地上停车位和 2 个地下停车位共需 1.4 万元。

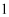请写出一个大于 $\text{[math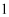]}$ 的无理数：．

如图，在平面直角坐标系中，点A（0，4）、B（﹣3，0），将线段AB沿x轴正方向平移n个单位得到菱形ABCD.

（1）画出菱形ABCD，并直接写出n的值及点D的坐标；
（2）已知反比例函数y＝ $\text{[math]}$ 的图象经过点D，▱ABMN的顶点M在y轴上，N在y＝ $\text{[math]}$ 的图象上，求点M的坐标；
（3）若点A、C、D到某直线l的距离都相等，直接写出满足条件的直线解析式.

一水果商某次按每千克3.2元购进一批苹果，销售过程中有20%的苹果正常损耗，为避免亏本，该水果商应将这批苹果的售价至少定为每千克元.

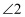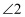下列四个图形中， $\text{[math]}$ 和 $\text{[math]}$ 不符合同位角定义的是（）．

A .

B .

C .

D .

某初中一个学期的数学总平均分是按扇形图信息要求进行计算的，该校胡军同学这个学期的数学成绩如下：则胡军这个学期数学总平均分为（　　）

胡军	平时作业	期中考试	期末考试
胡军	90	85	88

A . 87.5 B . 87.6 C . 87.7 D . 87.8

下列命题中正确的是（）

A . 任意两个等腰三角形都相似 B . 任意两个直角三角形都相似 C . 任意两个菱形都相似 D . 任意两个正方形都相似

为迎接中国

建党100周年，某校开展“学党史，知党恩，跟党走”的主题党史知识竞赛活动，学校随机抽取了部分参赛学生的成绩（得分均为整数）进行整理，并分别绘制如下不完整的统计图.

（1）补齐频数分布直方图，被抽样的学生人数有_▲_人；
（2）其中 $\text{[math]}$ ， $\text{[math]}$ ；
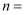（3）若该校共有 $\text{[math]}$ 名学生参加了此次党史知识竞赛，请估计该校党史知识竞赛成绩超过 $\text{[math]}$ 分的学生约有多少人？