七年级(初一)数学下学期下册试题
关于x的不等式 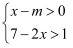 的整数解只有4个,则m的取值范围是( )
的整数解只有4个,则m的取值范围是( )
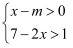 的整数解只有4个,则m的取值范围是( )
的整数解只有4个,则m的取值范围是( )
A . 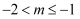 B .
B . 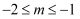 C .
C . 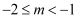 D .
D . 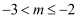
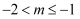 B .
B . 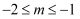 C .
C . 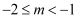 D .
D . 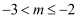
若关于 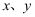 的二元一次方程组
的二元一次方程组 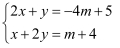 的解满足
的解满足 
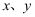 的二元一次方程组
的二元一次方程组 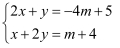 的解满足
的解满足 
-
(1) x-y=;x+y=(用含
 的代数式表示);
的代数式表示);
-
(2) 求
 的取值范围.
的取值范围.
若 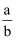 >0,
>0, 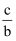 <0,则ac0.
<0,则ac0.
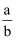 >0,
>0, 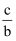 <0,则ac0.
<0,则ac0.
观察下列等式(式子中的“!”是一种运算符号):若1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,5!=5×4×3×2×1,…,则 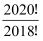 =.
=.
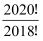 =.
=.
微信圈有篇热传的文章《如果想毁掉一个孩子,就给他一部手机》.为了解学生手机使用情况,西安高新区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查(问卷中的问题均为单项选择),并绘制①②统计图,在这次调查的学生中,手机使用目的为“玩游戏”的人数是35人.

请根据以上信息,解答下列问题:
-
(1) 在这次活动中被调查的学生共人;所抽取的学生使用手机时间的中位数落在范围内;
-
(2) 补全条形统计图;
-
(3) 该校共有学生4800人,请估算每周使用手机时间在2小时以上(不含2小时)的人数.
利用计算器求下列各式的值(结果精确到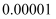 ):
):
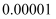 ):
):
-
(1)
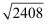 ;
;
-
(2)
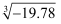 ;
;
-
(3)
 ;
;
-
(4)
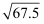 ;
;
-
(5)
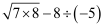 ;
;
-
(6)
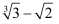 .
.
解二元一次方程组的基本思想是( )
A . 代入法
B . 加减法
C . 消元,化二元为一元
D . 由一个未知数的值求另一个未知数的值
求下列各数的立方根
-
(1) 729
-
(2) ﹣4
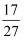
-
(3) ﹣
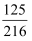
-
(4) (﹣5)3
下列实数,介于5和6之间的是( )
A . 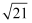 B .
B . 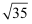 C .
C . 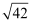 D .
D . 
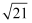 B .
B . 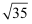 C .
C . 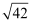 D .
D . 
“端午节”是我国的传统佳节,民间历来有吃粽子的习俗.某超市准备了515个豆沙粽,525个火腿粽和若干个腊肉棕,将这些粽子分成了A,B,C三类礼品盒进行包装.A类礼品盒里有4个豆沙粽,4个火腿粽和6个腊肉粽;B类礼品盒里有3个豆沙粽,5个火腿粽和6个腊肉粽;C类礼品盒里有6个豆沙粽,4个火腿粽和4个腊肉粽.已知A,B,C三类礼品盒的数量都为正整数,并且A类礼品盒少于44盒,B类礼品盒少于49盒.如果所有礼品盒里的腊肉粽的总个数为m,则m=
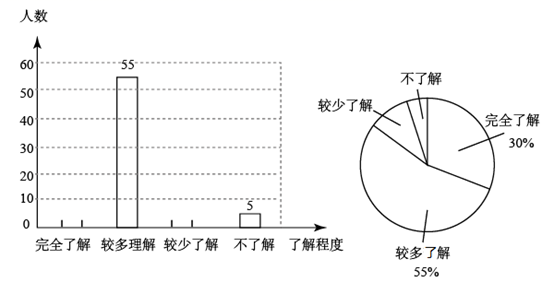
为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾”、“有害垃圾”、“可回收物”和“其他垃圾”这四类标准将垃圾分类处理调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制成如下统计图.
-
(1) 本次调查的样本容量是;
-
(2) 补全条形统计图;
-
(3) 已知该小区有居民2000人,请估计该小区对垃圾分类知识“完全了解”的居民人数.
如图,小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上,已知∠1=55°,则∠2的度数为( )
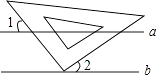
A . 45°
B . 35°
C . 55°
D . 125°
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分.
|
分组 |
家庭用水量x/吨 |
家庭数/户 |
|
A |
0≤x≤4.0 |
4 |
|
B |
4.0<x≤6.5 |
13 |
|
C |
6.5<x≤9.0 |
|
|
D |
9.0<x≤11.5 |
|
|
E |
11.5<x≤14.0 |
6 |
|
F |
x>14.0 |
3 |

根据以上信息,解答下列问题:
-
(1) 本次抽样调查的家庭数为户.
-
(2) 家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是;
-
(3) 家庭用水量的中位数在组.
-
(4) 若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
对于事件“抛一枚均匀硬币,落地后正面朝上”,它是( )
A . 必然事件
B . 随机事件
C . 确定事件
D . 不可能事件
全国文明城市创建期间,某校组织开展“垃圾分类”知识竞赛,共有25道题.答对一题记4分,答错(或不答)一题记-2分.小明参加本次竞赛得分要超过60分,他至少要答对道题.
取一张长方形纸片,过长方形的任意一个顶点将纸片折叠(只折一次),那么折痕和该顶点所在的长方形的两边所成角的关系是( )
A . 互余
B . 互补
C . 相等
D . 不确定
某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
-
(1) 甲乙两种材料每千克分别是多少元?
-
(2) 现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
-
(3) 在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
计算: 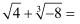 .
.
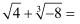 .
.
下列命题中,真命题的个数有( )
①如果不等式 的解集为
的解集为 , 那么
, 那么 ②已知二次函数
②已知二次函数 , 当
, 当 时,y随x的增大而减小③顺次连接对角线相等的四边形的四边中点所形成的图形是菱形④各边对应成比例的两个多边形相似
时,y随x的增大而减小③顺次连接对角线相等的四边形的四边中点所形成的图形是菱形④各边对应成比例的两个多边形相似
A . 1个
B . 2个
C . 3个
D . 4个
观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式” .
-
(1) 根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①71×=×17;②×594=495×.
-
(2) 设这类等式左边两位数的十位数字位a,个位数字为b,且a≥2,b≤9,写出表示“数字对称等式”一般规律的式子(含a,b),并证明.
最近更新
- ____________________________,大庇天下寒士俱欢颜,风雨不动安如山!(杜甫《茅屋为秋风所破歌》
- 果蝇的体细胞有8个染色体,在一般情况下,它的初级精母细胞、次级精母细胞、精子所含有的DNA分子数依次是 A 16 8
- 如图表示地壳中元素的含量(质量分数),图中y区域代表的元素是( )A.Si B.Fe C.O D.
- 气体甲能使湿润的红色石蕊试纸变蓝,气体乙可在空气中产生白雾,当甲与乙相遇时可生成白烟,这种白烟是() A.NH4Cl
- Dogs are social animals and withoutproper training, they wil
- 下列是某学生自己总结的一些规律,其中正确的是: A.氧化物不可能是还原产物,只可能是氧化产物 B.有些化学反应不属于化合
- 《十二铜表法》有这样的规定:“不得为任何个人的利益制定特别的法律”,“任何人非经审判,不得处死。”这体现了《十二铜表法》
- 在探究“导体的电阻跟哪些因索有关”的问题时,老师引导同学们做了如下实验:⑴猜想:导体电阻可能与导体长度横截面积_____
- You are saying thateveryone should be equal, and this is __
- 如图两条相交的直线OX、OY,,在射线OX、OY上分别再任意取A、B两点,作∠ABY的平分线BD,BD的反向延长线交的平
- 读我国各种运输方式的运输周转量构成表,完成下列问题。(1)占货运周转量比重最小的运输方式是______。该运输方式的主要
- (10·全国ⅠA篇)OPENING TIMES: 20 Mar to 19 Oct Mon to Sat: 9:00a
- Can you help ,please? A. me
- 小阅读语段训练:阅读下面语段,选出符合要求的一项地球上生命的历史也就是生物与它们的环境相互作用的历史。动植物的形体和习性
- 单词拼写1. The vegetable market isalways ___________ (拥挤) in the
- (1)如图1,△ABC内接于⊙O,AB为直径,∠CAE=∠B,试说明AE与⊙O相切于点A; (2)在图2中,若AB为非直
- 红细胞中Fe2+含量降低时,红细胞运输氧的能力相应减弱,这个事实说明Fe2+的作用是( ) A、调节血液的酸碱平
- 下列各组词语中加点的字是多音字,其中读音全都不相同的一组是( ) A.号角/名角 铁椎/脊椎骨
- (8分)全国著名发明家邹德俊发明了一种“吸盘式”挂衣钩,如图所示,将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物
- 图11所示的三个实验中,可以说明分子之间有相互作用力的是______图。 图10



