七年级(初一)数学下学期下册试题
平面直角坐标系上有一点 , 请根据题意回答下列问题:
, 请根据题意回答下列问题:
 , 请根据题意回答下列问题:
, 请根据题意回答下列问题:
-
(1) 若点P在x轴上,求出点P的坐标.
-
(2) 点Q的坐标为
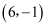 且
且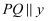 轴,求出点P的坐标.
轴,求出点P的坐标.
-
(3) 若点P到y轴的距离为2,直接写出a的值.
解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.

-
(1) 喜爱动画的学生人数和所占比例分别是多少?
-
(2) 请将条形统计图补充完整;
-
(3) 若该校共有学生2000人,依据以上图表估计该校喜欢体育的人数约为多少?
关于  的不等式组
的不等式组 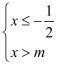 的所有整数解的积为2,则
的所有整数解的积为2,则  的取值范围为( )
的取值范围为( )
 的不等式组
的不等式组 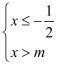 的所有整数解的积为2,则
的所有整数解的积为2,则  的取值范围为( )
的取值范围为( )
A . 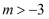 B .
B . 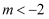 C .
C . 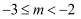 D .
D . 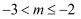
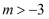 B .
B . 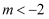 C .
C . 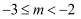 D .
D . 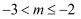
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1 +∠2 = 90°.

求证:
-
(1) AB∥CD;
-
(2) 求证:∠2 +∠3 = 90°;
实数4的平方根是( )
A . 2
B . -2
C . ±2
D . 16
一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A . 第一次向右拐40°,第二次向左拐140°
B . 第一次向左拐40°,第二次向右拐40°
C . 第一次向左拐40°,第二次向右拐140°
D . 第一次向右拐40°,第二次向右拐40°
如图,两条平行线a,b被直线c所截,若∠2=2∠1,则∠2等于( )
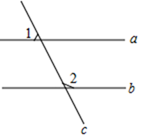
A . 60°
B . 110°
C . 120°
D . 150°
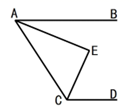
如图,  ,
, 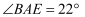 ,
, 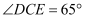 ,求
,求 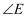 .
.
 ,
, 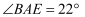 ,
, 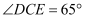 ,求
,求 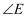 .
.
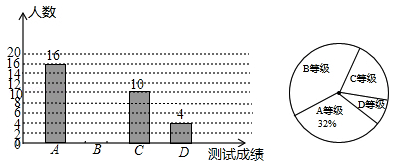
某中学为了了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图;
-
(1) 这次抽样调查的样本容量是,并补全条形图;
-
(2) D等级学生人数占被调查人数的百分比为,在扇形统计图中C等级所对应的圆心角为°;
-
(3) 该校九年级学生有1500人,请你估计其中A等级的学生人数.
一个正方体的体积为125cm3 , 则这个正方体的表面积为cm2 .
计算: 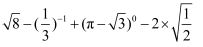
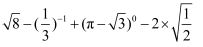
为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )

A . 众数是80千米/时,中位数是60千米/时
B . 众数是70千米/时,中位数是70千米/时
C . 众数是60千米/时,中位数是60千米/时
D . 众数是70千米/时,中位数是60千米/时
世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.0000000076克,将数0.0000000076用科学记数法表示为( )
A . 7.6×10﹣9
B . 7.6×10﹣8
C . 7.6×109
D . 7.6×108
如图在正方形网格中,若A(1,1),B(2,0),则C点的坐标为( )

A . (-3,-2)
B . (3,-2)
C . (-2,-3)
D . (2,-3)
解下列方程(组)
-
(1)
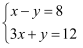
-
(2)
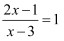
不透明袋子中有1个红球和2个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,恰好是红球的概率为.
正比例函数 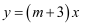 ,
,  随
随  的增大而增大,那么
的增大而增大,那么  的取值范围是.
的取值范围是.
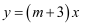 ,
,  随
随  的增大而增大,那么
的增大而增大,那么  的取值范围是.
的取值范围是.
我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:

-
(1) 将条形统计图补充完整;
-
(2) 扇形图中的“1.5小时”部分圆心角是多少度?
-
(3) 求抽查的学生劳动时间的众数、中位数.
计算:(﹣1)2﹣  =.
=.
 =.
=.
随着微电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.0000007(平方毫米),这个数用科学记数法表示为( )
A . 7×10-6
B . 0.7×10-6
C . 7×10-7
D . 70×10-8
最近更新
- 如图所示,物体A的质量是B的2倍,中间有一压缩弹簧,放在光滑水平面上,由静止同时放开两物体后一小段时间内( ) A
- 下图中hl、h2为某地一建筑在一年中正午时影子长度的变化范围,hl<h2,S、N表示方向。读图,回答11题。11.
- 在一恒温恒容容器中,发生反应:2A(g)+B(s) ⇌ C(g)+D(g),下列描述中能表明反应已达到平衡状态的有(
- 党的八大的召开,标志着中国探索自己的建设社会主义的道路取得初步的成果。中国在第八次全国代表大会确定的主要任务是(
- 下列关于呼吸作用产物的叙述中,只适用于有氧呼吸的是 ( ) A.产生ATP B.产生丙酮酸 C
- 已知向量=(2,4),=(﹣1,1),则2﹣=() A.(5,7) B.(5,9) C.(3,7) D.(3,9)
- 不少中小学生喜食油炸薯条。但是,油炸薯条易产生一种叫丙烯酰胺的致癌物,长期摄入易引发多种疾病,其结构为:,据此,不能推断
- 环境中影响生物形态、生理、分布的因素称为 。它又区分为 和
- 阅读下面两则材料,按要求作文 。 材料一:某名牌大学毕业的小王进了一家公司。当领导分配她做最基础的工作时,原本很有优越感
- 已知函数满足,对于任意都有,且,求函数的表达式.
- 选出依次填入下列句子横线处词语恰当的一项( )。 ①他眼睛里的那个黑夜的世界,渐渐地泛起淡淡的光,像银亮的雾_____
- 一个多项式加上得到,则这个多项式是 .
- 17、生活中处处有化学,下列说法不合理的是( ) A. 铝可用于制导线 B. 药品可治病,多用也无妨 C. 缺铁易
- 近期,科学家利用“单倍体干细胞”, 通过神奇的细胞“变性手术”, 仅利用两个雌性动物的卵子就实现不如动物的繁衍,打破了人
- Heis often the last student _______________ to school. A.
- 从圆外一点P(3,2)向这个圆作两条切线,则两切线夹角的余弦值为 (A)
- 除了…之外还有
- 按如图所示的运算程序.能使翰出结果为3的,X,Y的值是A. x=5.y=一2 B,X=3.,y=一3 C. x=一4.y
- 如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距l=1m,两轨道之间用R=3Ω的电阻连接,一质量m=0.5kg
- 图1为25℃环境中甲、乙两种植物在不同光照强度下CO2吸收量的变化曲线,图2表示在一定光照强度下温度对图1中一种植物二氧



