七年级(初一)数学下学期下册试题
-
(1) 计算:
 -|-2|+(
-|-2|+(  )0-(-1)
)0-(-1)
-
(2) 化简:(x-1)2-x(x+7)
在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于.
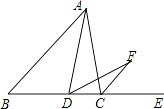
如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.
-
(1) 求证:CF∥AB;
-
(2) 若∠CAD=20°,求∠CFD的度数.
已知方程组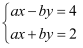 的解为
的解为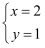 ,则
,则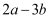 的值为( )
的值为( )
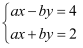 的解为
的解为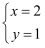 ,则
,则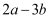 的值为( )
的值为( )
A .  B .
B .  C .
C . 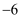 D .
D . 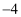
 B .
B .  C .
C . 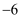 D .
D . 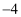
如果a<b , 那么下列不等式中错误的是( )
A . a+2<b+2
B . 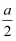 <
<  C . ﹣4a<﹣4b
D . 3a﹣1<3b﹣1
C . ﹣4a<﹣4b
D . 3a﹣1<3b﹣1
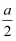 <
<  C . ﹣4a<﹣4b
D . 3a﹣1<3b﹣1
C . ﹣4a<﹣4b
D . 3a﹣1<3b﹣1
已知方程 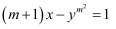 是关于x,y的二元一次方程,则m=.
是关于x,y的二元一次方程,则m=.
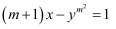 是关于x,y的二元一次方程,则m=.
是关于x,y的二元一次方程,则m=.
若  是一个完全平方式,则m的值是( )
是一个完全平方式,则m的值是( )
 是一个完全平方式,则m的值是( )
是一个完全平方式,则m的值是( )
A . 10
B . —10
C . -6或10
D . 10或—10
如图,已知AE//BD,∠1=3∠2,∠2=26°,则∠C=

在平面直角坐标系中,有一条线段AB,已知点A(﹣3,0)和B(0,4),平移线段AB得到线段A1B1 . 若点A的对应点A1的坐标为(0,﹣1),则线段AB平移经过的区域(四边形ABB1A1)的面积为( )
A . 12
B . 15
C . 24
D . 30
解方程组: 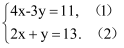
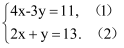
下列图形中,线段 的长表示点A到直线
的长表示点A到直线 的距离的是( )
的距离的是( )
 的长表示点A到直线
的长表示点A到直线 的距离的是( )
的距离的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系中,△OAB的顶点坐标分别为(0,0),A(2,1),B(1,﹣2).

-
(1) 以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 , 使它与△OAB的位似比为2:1,并分别写出点A,B的对应点A1、B1的坐标;
-
(2) 画出将△OAB向左平移2个单位,再向上平移1个单位后得△O2A2B2 , 并写出点A,B的对应点A2、B2的坐标;
-
(3) 判断△OA1B1和△O2A2B2是位似图形吗?若是,请在图中标出位似中心 M,并写出点M的坐标.
如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y= 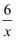 (x>0)的图象上,此时点A移动的距离为.
(x>0)的图象上,此时点A移动的距离为.
一滴水重0.00005千克.用科学记数法表示这个数是( )千克.
A . 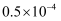 B .
B . 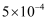 C .
C .  D .
D . 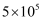
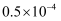 B .
B . 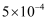 C .
C .  D .
D . 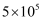
解不等式组 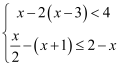 并写出它的整数解.
并写出它的整数解.
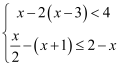 并写出它的整数解.
并写出它的整数解.
某商场筹集资金12.8万元,一次性购进空调、彩电共30台,根据市场需要,这些空调,彩电可以全部销售,计划全部销售后利润不少于2.25万元,其中空调,彩电的进价和售价见表格:
|
空调 |
彩电 |
|
|
进价(元/台) |
5000 |
3200 |
|
售价(元/台) |
5800 |
3900 |
设商场计划购进空调x台
-
(1) 空调和彩电全部销售后商场获得的利润为y元,求出y与x的函数关系式;
-
(2) 商场有哪几种进货方案可供选择?
-
(3) 由于商场的空调进行了促销活动,实际空调获利只有计划的80%,按原计划的哪个进货方案,商场获利最大?最大利润是多少元?
如果 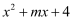 是一个完全平方式,则
是一个完全平方式,则  等于( )
等于( )
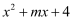 是一个完全平方式,则
是一个完全平方式,则  等于( )
等于( )
A . -4
B . 2
C . 4
D . ±4
满足不等式﹣  x+1≥0的非负整数解是.
x+1≥0的非负整数解是.
 x+1≥0的非负整数解是.
x+1≥0的非负整数解是.
已知方程组 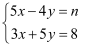 中,x,y的值相等,则n=.
中,x,y的值相等,则n=.
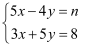 中,x,y的值相等,则n=.
中,x,y的值相等,则n=.
下列调查中,不适合用抽样调查方式的是( )
A . 调查“神舟十一号”飞船重要零部件的产品质量
B . 调查某电视剧的收视率
C . 调查一批炮弹的杀伤力
D . 调查一片森林的树木有多少棵
最近更新
- 各式各样的剪刀都是一对对杠杆,如图8-A-4所示。要剪开较硬的物体,使用哪种剪刀最合适 【 】
- 下列过程中发生了化学变化的是 () A.瓷碗
- 已知NaHSO4在水中的电离方程式为:NaHSO4==Na++H++SO某温度下向pH=6的蒸馏水中加入NaHSO4晶体
- 在一对性状的正交与反交实验中,F1 往往能得出不同结果的一组遗传方式是 ( ) A.细胞核遗传与细胞质遗传
- 下列各组词语中加点的字,读音都不相同的一组是( ). A.费解/解数 蔓延/顺蔓摸瓜 商贾/
- 1945年8月15日12时,日本广播电台传出低沉的声音:“帝国政府已受旨通知美、英、中、苏四国政府,我帝国接受彼等联合宣
- 已知函数时的值域为,则的取值范围是( ) A. B. C.
- 最近科学家获得了一种稳定性好、抗氧化能力强的活化化合物,其结构如下:在研究其性能的过程中,发现结构片段X对化合物A的性能
- 阅读下面的文字,根据要求作文。 面对万象尘世,法国作家巴尔扎克说:“拼着一切代价,奔你的前程”。 美国作家卡耐基认为:对
- 以枪乌贼的粗大神经纤维作材料,在神经纤维某处的细胞膜内外放置电极a和b(如下左图),在图中M点给予一次适宜刺激.通过电压
- 已知曲线C的参数方程是(θ为参数),则曲线C不经过第二象限的一个充分不必要条件是
- 下列句子中,加点的成语使用恰当的一句是( )(3分) A.中华民族自古以来便具有扶助他人的热肠,做善事,行义举,从
- 沼气是我国农村地区积极推广的新能源之一。就沼气开发利用与气候条件的关系,下列叙述正确的是( ) A.北方比南方日
- 下列关于视角的说法中,正确的是( )A.视角越大,我们看到的物体越清晰B.视角越小,我们看到的物体越清晰C.视角过大或过
- 下列递变规律正确的是 A.C、N、O最高正价依次升高 B.钠、镁、铝的还原性依次减弱 C.HC1、HBr、HI的稳定性依
- 阅读下面的文言文,完成下列小题。 宋太初,泽州晋城人。太平兴国三年,举进士,解褐大理评事、通判戎州,以善政闻。有诏褒美,
- 若p:x∈R.x2≥0,q:=x3,下面命题中的假命题为()①命题p ②若q则p ③﹁p ④p∧qA.①③
- 能正确表示下列反应的离子方程式是 ( ) A.过氧化钠固体与水反应:2O22—+2H2O == 4OH-+O2↑B.
- 某化合物与硫酸反应生成硫酸钾、水、二氧化碳,该化合物可能是 A.氢氧化钾
- (18分)I.某天然有机化合物A仅含C、H、O元素,与A相关的反应框图如下:(1)写出下列反应的反应类型: B→D



