已知在四棱锥中，底面是矩形，且 分别是线段的中点．

（Ⅰ）判断并说明上是否存在点，使得∥平面；

（Ⅱ）若与平面所成的角为，求二面角的平面角的余弦值．

设，，若是与的等比中项，则的最小值是（   ）

A．         B．       C.         D．

设随机变量服从正态分布，则下列结论不正确的是：(      )

A.   B.

C.         D.

如果函数,那么函数是（    ）．

A．奇函数,且在(-∞，0)上是增函数  

B．偶函数,且在(-∞，0)上是减函数

C．奇函数,且在(0，+∞)上是增函数   

D．偶函数,且在(0，+∞)上是减函数

设双曲线 (a>0，b>0)的虚轴长为2，焦距为2，则双曲线的渐近线方程为(　　)

A．y＝±x         B．y＝±2x         C．y＝±x           D．y＝±x

根据如图2的框图，当输入为6时，输出的（　　）

A．1    B．2    C．5    D．10

已知抛物线y²＝4x截直线y＝2x＋m所得弦长|AB|＝3.

(1)求m的值；

(2)设P是x轴上的点，且△ABP的面积为9，求点P的坐标．

某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动，组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查。调查结束后，学生会对问卷结果进行了统计，并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表：

(1)求上表中的m，n的值，并补全右图所示的频率直方图；

(2)在被调查的居民中，若从年龄在[10，20)，[20，30)的居民中各随机选取1人参加垃圾分类知识讲座，求选中的两人中仅有一人不知道垃圾分类方法的概率。

设点，若在圆上存在点，使得，则的取值范围是

A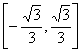．   B.    C.    D.

在正方体中，是棱的中点，是侧面内的动点，且∥平面，记与平面所成的角为，下列说法错误的是（    ）

A.点的轨迹是一条线段     B.与不可能平行

C.与是异面直线     D.

我国天文学和数学著作《周髀算经》中记载；一年有二十四个节气，每个节气的晷长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测量影子的长度）.二十四节气及晷长变化如图所示，相邻两个节气晷长减少或增加的量相同，周而复始.已知每年冬至的晷长为一丈三尺五寸，夏至的晷长为一尺五寸（一丈等于十尺，一尺等于十寸），则说法不正确的是（   ）

A．相邻两个节气晷长减少或增加的量为一尺                    B．春分和秋分两个节气的晷长相同

C．立春的晷长与立秋的晷长相同                                     D．立冬的晷长为一丈五寸

已知椭圆为椭圆的左.右焦点,是椭圆上任一点,若的取值范围为,则椭圆方程为（　　）

A．    B．    C．    D．

若两个正实数满足，且不等式有解，则实数的取值范围______.

已知函数的图象在点处的切线方程为，

则函数的解析式                           ；

已知=2求下列各式的值:
(1);(2)

在锐角中，角，，的对边分别为，，，若，则的最小值为

A．                 B．                C．                  D．

已知椭圆的半焦距为，左焦点为F，右顶点为A，抛物线与椭圆交于B，C两点，若四边形ABFC是菱形，则椭圆的离心率是

A.               B.              C.               D .

执行如图1所示的程序框图,若输入的值为10，则输出S的值是

A．45         B．46         C．55         D．56

已知，又函数是上的奇函数，则数列的通项公式为（     ）

A.            B.               C.            D.

已知抛物线y²=2px（p＞0）的焦点F位于直线x+y﹣1=0上．

（Ⅰ）求抛物线方程；

（Ⅱ）过抛物线的焦点F作倾斜角为45°的直线，交抛物线于A，B两点，求线段AB的中点C的横坐标．