已知过原点的动直线与圆相交于不同的两点，.

（1）求圆的圆心坐标；

（2）求线段的中点的轨迹的方程；

（3）是否存在实数,使得直线与曲线只有一个交点？若存在，求出的取值范围；若不存在，说明理由.

已知，

（I）求的值；

（II）求的值；

若关于的方程有两个不同的实数解，则实数的取值范围是（    ）

A.      B.            C.            D.    

下列图形不一定是平面图形的是(    )

A. 三角形    B. 四边形    C. 圆    D. 梯形

如图，在△ABC中， =，P是BN上的一点，若=m+，则实数m的值为　　　　　　．

 已知命题p：，命题q：，若“”为真命题，求实数a的取值范围。

复数等于                                                           (  　)

A．1＋i                         B．1－i

C．－1＋i                       D．－1－i

在正方体中，分别为棱的中点，则在空间中与三条直线都相交的直线有

  A．无数条     B．　３条　　　Ｃ．１条　　Ｄ． 0条

某工厂随机抽取部分工人调查其上班路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），若上班路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．
（1）求直方图中a的值；
（2）如果上班路上所需时间不少于1小时的工人可申请在工厂住宿，若招工2400人，请估计所招工人中有多少名工人可以申请住宿；
（3）该工厂工人上班路上所需的平均时间大约是多少分钟．

.

.

如果执行右面的程序框图，那么输出的（　 　）

A、22           B、46           C、       D、190

．如图所示，有5组(x，y)数据，去掉__ ____组数据后，剩下的4组数据的线性相关性最大．

某种设备的使用年限(年)和维修费用(万元),有以下的统计数据:

（Ⅰ）画出上表数据的散点图；

（Ⅱ）请根据上表提供的数据，求出关于的线性

回归方程；

（Ⅲ）估计使用年限为10年，维修费用是多少万元？

（附：线性回归方程中，其中，）．

若在曲线上两个不同点处的切线重合，则称这条切线为曲线 

     的 “自公切线”．下列方程：

     ①；  ②；    ③；     ④．

     对应的曲线中存在“自公切线”的有　      　（用序号作答）．

命题“”的否定是                                       （    ）

A．   B．    C．  D． 

已知椭圆的左右焦点分别为F₁,F₂，过右焦点F₂的直线AB与椭圆交于A，B两点，则△ABF₁的周长为_____________.

已知数列中，，则数列的通项公式为___ ___；

若，则的最大值___ ___.

设等差数列满足，，

（1）求的通项公式；

（2）设的前项和为，求满足成立的值。

已知函数f（x）=sinx，x∈（0，2π），点P（x，y）是函数f（x）图象上任一点，其中0（0，0），A（2π，0），记△OAP的面积为g（x），则g′（x）的图象可能是（　　）

A．   B．   C．   D．

试通过建立空间直角坐标系，利用空间向量解决下列问题：

如图，已知四边形ABCD和BCEF均为直角梯形，AD∥BC，CE∥BF，且∠BCD=∠BCE=90°，平面ABCD⊥平面PCEF，BC=CD=CE=2AD=2BF=2

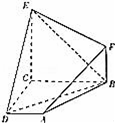（Ⅰ）证明：AF∥平面BDE

（Ⅱ）求锐二面角A﹣DE﹣B的余弦值．