探究弹力和弹簧伸长的关系 知识点题库

回答下列问题:
-
(1) 本实验中可认为,弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等.已知重力加速度大小为g.为求得Ek,至少需要测量下列物理量中的 (填正确答案标号).A . 小球的质量m B . 小球抛出点到落地点的水平距离s C . 桌面到地面的高度h D . 弹簧的压缩量△x E . 弹簧原长l0
-
(2) 用所选取的测量量和已知量表示Ek , 得Ek=.
-
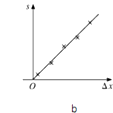
(3) 图b中的直线是实验测量得到的s﹣△x图线.从理论上可推出,如果h不变,m增加,s﹣△x图线的斜率会(填“增大”、“减小”或“不变”);如果m不变,h增加,s△x图线的斜率会(填“增大”、“减小”或“不变”).由图乙中给出的直线关系和Ek的表达式可知,Ep与△x的次方成正比.
由胡克定律可知,在弹性限度内,弹簧的弹力F与形变量x成正比,其比例系数与弹簧的长度、横截面积及材料有关.因而同学们猜想,悬索可能也遵循类似的规律.
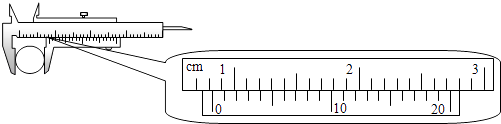
①同学们通过游标卡尺测样品的直径来测截面积,某次测量结果如图所示,则样品直径为 cm.
②经过同学们充分的讨论,不断完善实验方案,最后实验取得数据如下:
样 品 | 拉力F 伸长量x 截面积S 长 度L | 200N | 400N | 600N | 800N | |
样品A | 1m | 0.50cm2 | 0.02cm | 0.04cm | 0.06cm | 0.08cm |
样品B | 2m | 0.50cm2 | 0.08cm | 0.16cm | 0.24cm | 0.32cm |
样品C | 1m | 1.00cm2 | 0.01cm | 0.02cm | 0.03cm | 0.04cm |
样品D | 3m | 0.50cm2 | 0.18cm | 0.36cm | 0.54cm | 0.72cm |
样品E | 1m | 0.25cm2 | 0.04cm | 0.08cm | 0.12cm | 0.32cm |
A.分析样品C的数据可知:拉力F(单位:N)与伸长量x(单位:m)遵循的函数关系式是.
B.对比各样品实验数据可知:悬索受到的拉力F=kx,比例系数k与成正比、与悬索的截面积s的大小成.
根据曲线可以计算出这种规格弹簧的劲度系数为N/m.

-
(1) 他通过实验得到如图乙所示的弹力大小F与弹簧长度L的关系图线.由此图线可得该弹簧的原长L0=cm,劲度系数k=N/m.
-
(2) 他又利用本实验原理把该弹簧做成一把弹簧测力计,当弹簧测力计上的示数如图丙所示时,该弹簧的长度L=cm.

-
(1) 关于实验操作,卜列说法正确的是________A . 刻度尺竖直放在弹簧附近,零刻度线与弹簧上端对齐 B . 实验过程要保证弹簧竖直且静止 C . 悬挂的钩码越多,测出数据越多,实验误差越小 D . 如果弹簧上指针上下振动,可在指针运动最快的位置进行读数
-
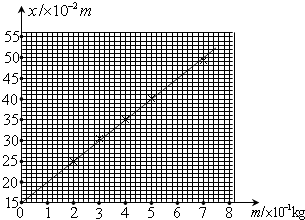
(2) 该同学用a、b两条不同的弹簧进行实验,多次改变钩码的质量,测出相应的弹簣的长度L,画出m-L图象如图所示,由图象可知,a弹簧的原长(填“大于”、“小于”或“等于”)b弹簧的原长,a弹簧的劲度系数(填“大于”、“小于”或“等于”)b弹簧的劲度系数,由图象得到的弹簧原长(填“大于”、“小于”或“等于”)实际原长。

 和
和  的B、C两段,设B段的劲度系数为k2、C段的劲度系数为k3 , 关于k1、k2、k3的大小关系,同学们做出了如下猜想:
的B、C两段,设B段的劲度系数为k2、C段的劲度系数为k3 , 关于k1、k2、k3的大小关系,同学们做出了如下猜想: 甲同学:既然是同一根弹簧截成的两段,所以, 
乙同学:同一根弹簧截成的两段,越短劲度系数越大,所以, 
丙同学:同一根弹簧截成的两段,越长劲度系数越大,所以, 
-
(1) 为了验证猜想,可以通过实验探究来完成。实验所需的器材除铁架台外,还必需的器材有________(填下列器材名称前的代号)。A . 天平 B . 质量已知(且质量相等)的钩码若干 C . 打点计时器 D . 刻度尺
-
(2) 如图所示,是通过实验得到的图线。根据图线可知:(填“甲”或“乙”或“丙”)同学的猜想是正确的。

 ,现要测出弹簧的原长
,现要测出弹簧的原长  和弹簧的劲度系数,该同学通过改变
和弹簧的劲度系数,该同学通过改变  而测出对应的弹力F,作出F-
而测出对应的弹力F,作出F-  图象如图乙所示,则弹簧的劲度系数为k=N/m,弹簧的原长
图象如图乙所示,则弹簧的劲度系数为k=N/m,弹簧的原长  =cm.
=cm.

-
(1) 将表格中的两个数据补齐;
钩码质量m/g
0
30
60
90
12
150
弹簧总长度l/cm
6.0
7.2
8.3
9.5
10.6
11.8
弹力F/N
0
0.3
0.6
1.2
1.5
弹簧伸长量x/m
0
0.012
0.023
0.046
0.058
-
(2) 根据实验数据在坐标纸上作出弹力F跟弹簧伸长量关系的F-x图象;
-
(3) 要根据F-x图象计算出弹簧的劲度系数为k=N/m(结果保留2位有效数字),此弹簧的弹力大小F弹跟弹簧伸长量x的关系是。
 。主要步骤如下:
。主要步骤如下: 
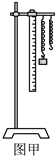
A.将铁架台置于水平桌面上,按图装好器材
B.记下弹簧自由下垂时,其下端指针在刻度尺上所示刻度了l0=10.00cm
C.以F为纵坐标,x为横坐标,做出F-x图线
D.依次在弹簧下端挂上1个、2个、3个、4个…钩码,分别记录钩码静止时,弹簧下端指针对应的刻度l,然后取下钩码
E.根据图线写出F与x的关系式,并解释关系式中常数的意义
-
(1) 以上操作的合理顺序是(填步骤前字母);
-
(2) 该同学在弹簧下端挂1.50N的钩码时,指针在刻度尺上指示位置如图乙所示,则弹簧的伸长量x3=cm;
-
(3) 将x3对应的点描到图丙的坐标系中,连同其他数据点作出F-x图线;
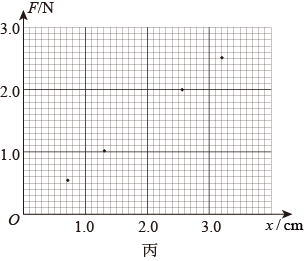
-
(4) 由图线可求得弹簧的劲度系数k=N/m。(结果保留两位有效数字)
-
(1) 在安装刻度尺时,必须使刻度尺保持状态;
-
(2) 关于该实验的说法,正确的是___________A . 所挂钩码的个数是没有限制的 B . 测量弹簧中弹力的依据是二力平衡 C . 测量弹簧原长时应将弹簧水平放置 D . 根据所测数据在F-x图上描点,作图像时应用折线连接每一个数据点
-
(3) 某轻弹簧的弹力大小F与弹簧长度l的关系图像如图乙所示,

由此图线可得该弹簧的原长是cm;劲度系数k=N/m。
-
(4) 现将两根相同的弹簧串联起来,如图丙所示,若单根弹簧的弹力F与伸长量x的关系图像,如图丁中图线①所示,则串联后的整根长弹簧的弹力F与伸长量x的图像可能是___________
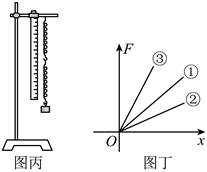 A . 图线① B . 图线② C . 图线③ D . 均有可能
A . 图线① B . 图线② C . 图线③ D . 均有可能
|
钩码质量m/g |
0 |
10 |
20 |
30 |
40 |
50 |
|
弹簧总长度l/cm |
3.00 |
3.50 |
4.00 |
4.50 |
5.00 |
5.50 |
|
弹力大小F/N |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |

-
(1) 关于本实验,下列说法正确的是___________。A . 悬吊钩码时,应在钩码静止后再读数 B . 应在弹簧的弹性限度范围内进行测量 C . 在安装刻度尺时,必须使刻度尺保持竖直状态 D . 在测量弹簧原长时,应将弹簧平放在水平桌面上,使其自然伸长,并测出其长度
-
(2) 根据上述实验数据,在图乙所示的坐标纸上,作出弹簧弹力大小F跟弹簧总长度l之间的关系图像,并求出该弹簧的劲度系数k= N/m;
-
(3) 一个实验小组在“探究弹力和弹簧伸长量的关系”的实验中,使用两条不同的轻质弹簧a和b,得到弹力和弹簧长度的图像如图丙所示。下列表述正确的是(______)A . a的原长比b的短 B . a的劲度系数比b的小 C . a的劲度系数比b的大 D . 测得的弹力与弹簧的长度成正比
-
(1) 将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在方向(填“水平”或“竖直”)。
-
(2) 弹簧自然悬挂,待弹簧稳定时,长度记为L0 , 弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10 g砝码,弹簧长度依次记为L1至L6 , 数据如下表:
代表符号
L0
Lx
L1
L2
L3
L4
L5
L6
数值(cm)
25.35
27.35
29.35
31.30
33.4
35.35
37.40
39.30
表中有一个数值记录不规范,代表符号为。
-
(3) 如图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与的差值(填“L0或Lx”)。
-
(4) 由图可知弹簧的劲度系数为N/m;通过图和表可知砝码盘的质量为g(结果保留两位有效数字,重力加速度取10m/s2)。

-
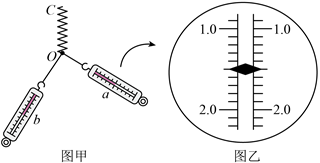
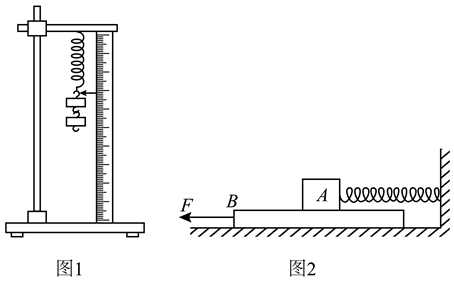
(1) 若弹簧秤a、b间夹角为90°,弹簧秤a的读数是N(图乙中所示),则弹簧秤b的读数可能为N。
-
(2) 保持弹簧秤a与弹簧OC的夹角不变,将弹簧秤a、b间的夹角逐渐从90°增大至120°,则在此过程中(________)A . 弹簧秤a的读数变大,弹簧秤b的读数变大 B . 弹簧秤a的读数变大,弹簧秤b的读数变小 C . 弹簧秤a的读数变小,弹簧秤b的读数变大 D . 弹簧秤a的读数不变,弹簧秤b的读数变小
 。
。 
-
(1) 测劲度系数的实验步骤:
a.将轻弹簧悬挂在铁架台的横杆上,将刻度尺竖直固定在轻弹簧旁将刻度尺的零刻度与轻弹簧的上端对齐;
b.在弹簧下端依次挂上不同质量的钩码,记录每次钩码的总质量m及对应指针所指刻度值x;
c.在
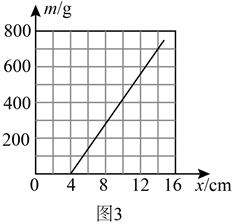
 坐标系上描点作图,作出的图像如图3所示。
坐标系上描点作图,作出的图像如图3所示。由图像可知,弹簧的原长

 ,弹簧的劲度系数
,弹簧的劲度系数 
 。
。
-
(2) 用图2所示装置测动摩擦因数,长木板B放在水平面上,物块A放在长木板上,并用(1)问中轻弹簧将物块A与竖直墙面连接,弹簧保持水平,用水平力F拉长木板B向左运动,A保持静止,测得这时弹簧的长度为
 ,已知物块A的质量为
,已知物块A的质量为  ,则物块A与长木板间的动摩擦因数
,则物块A与长木板间的动摩擦因数 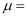 ;实验中由于弹簧悬挂时的原长比平放时的自然长度长,因此实验测得的动摩擦因数比实际值偏(填“大”或“小”)。
;实验中由于弹簧悬挂时的原长比平放时的自然长度长,因此实验测得的动摩擦因数比实际值偏(填“大”或“小”)。
-
(1) 某同学在做该实验时,通过处理数据得到了图甲所示的
 图像,其中
图像,其中  为弹簧弹力,
为弹簧弹力,  为弹簧长度。请通过图甲来分析并计算,该弹簧的原长
为弹簧长度。请通过图甲来分析并计算,该弹簧的原长 
 ,弹簧的劲度系数
,弹簧的劲度系数 
 ;
; 
-
(2) 另一位同学使用两条不同的轻质弹簧
 和
和  得到弹力与弹簧长度的图像如图乙所示,下列表述正确的是__________。
A .
得到弹力与弹簧长度的图像如图乙所示,下列表述正确的是__________。
A . 的原长比
的原长比  的短
B .
的短
B .  的劲度系数比
的劲度系数比  的大
C .
的大
C .  的劲度系数比
的劲度系数比  的小
的小
-
(1) 甲同学在做该实验时,通过处理数据得到了图甲所示的
 图像,其中
图像,其中  为弹簧弹力,
为弹簧弹力,  为弹簧长度。请通过图甲,分析并计算弹簧的劲度系数
为弹簧长度。请通过图甲,分析并计算弹簧的劲度系数 
 。该同学将该弹簧制成一把弹簧测力计,当弹簧测力计的示数如图乙所示时,该弹簧的长度
。该同学将该弹簧制成一把弹簧测力计,当弹簧测力计的示数如图乙所示时,该弹簧的长度 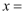 cm。
cm。 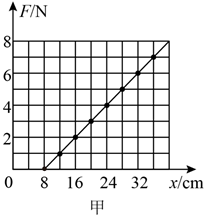
-
(2) 乙同学使用两条不同的轻质弹簧a和b,得到弹力与弹簧长度的关系图像如图丙所示。下列表述正确的是___________。
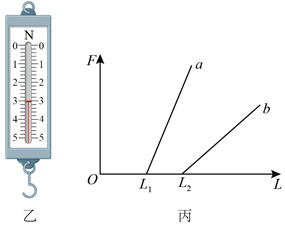 A . a的原长比b的长 B . a的劲度系数比b的大 C . a的劲度系数比b的小 D . 测得的弹力与弹簧的长度成正比
A . a的原长比b的长 B . a的劲度系数比b的大 C . a的劲度系数比b的小 D . 测得的弹力与弹簧的长度成正比
-
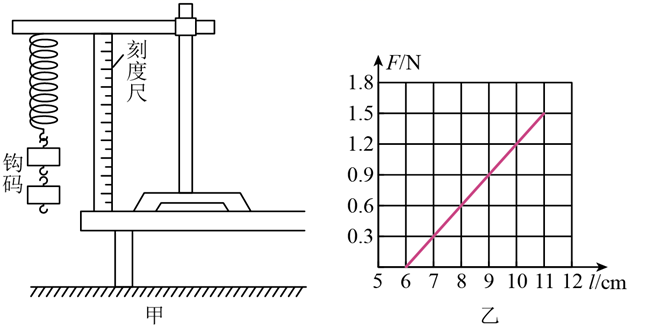
(1) 在安装刻度尺时,必须使刻度尺保持状态。
-
(2) 由图乙中的图线求得该弹簧的劲度系数为k= N/m。
-
(3) 另一同学在做此实验时,先把弹簧平放在桌面上使自然伸长,用毫米刻度尺测出弹簧伸长后的长度L0 , 再把弹簧竖直悬挂起来,挂上钩码后测出弹簧伸长后的长度L,把L-L0作为弹簧的伸长量x,这样操作,由于弹簧自身重力的影响,最后画出图线可能是____。A .
 B .
B . 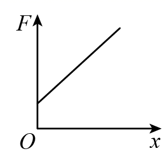 C .
C . 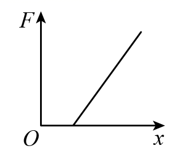 D .
D . 
 、
、 。在坐标纸上画出
。在坐标纸上画出 、
、 与钢球个数n的关系
与钢球个数n的关系 图像,如图乙所示。忽略摩擦,重力加速度g取
图像,如图乙所示。忽略摩擦,重力加速度g取 , 则下列说法正确的是( )
, 则下列说法正确的是( )
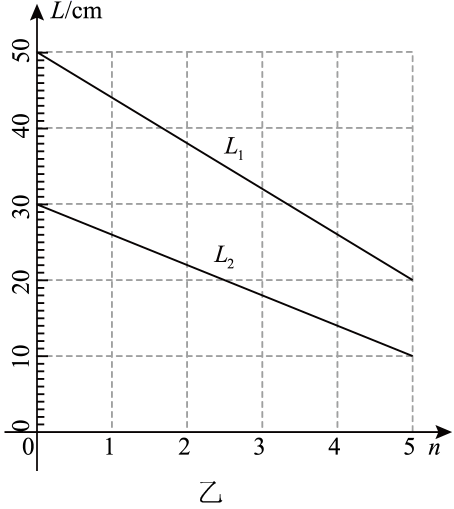
 时,弹簧1和弹簧2的形变量相同
C . 弹簧1的劲度系数为50N/m
D . 弹簧2的劲度系数为
时,弹簧1和弹簧2的形变量相同
C . 弹簧1的劲度系数为50N/m
D . 弹簧2的劲度系数为

实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
悬挂钩码个数 | 1 | 2 | 3 | 4 | 5 | 6 |
弹簧弹力F/N | 0.49 | 0.98 | 1.47 | 1.96 | 2.45 | 2.94 |
弹簧伸长量x/cm | 2.00 | 3.90 | 5.80 | 8.00 | 9.90 | 12.00 |
-
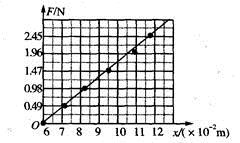
(1) 在如图1所示的坐标纸上已经描出了其中5次弹簧弹力F与弹簧伸长量x对应的数据点,请把第4次测量的数据对应点描绘在坐标纸上,并作出弹簧弹力与弹簧伸长量的F-x图线;

-
(2) 观察F-x图线,可以判断在弹性限度内,弹簧弹力大小F与弹簧伸长量x成正比关系,其依据是。其中F-x图线斜率的物理意义是;
-
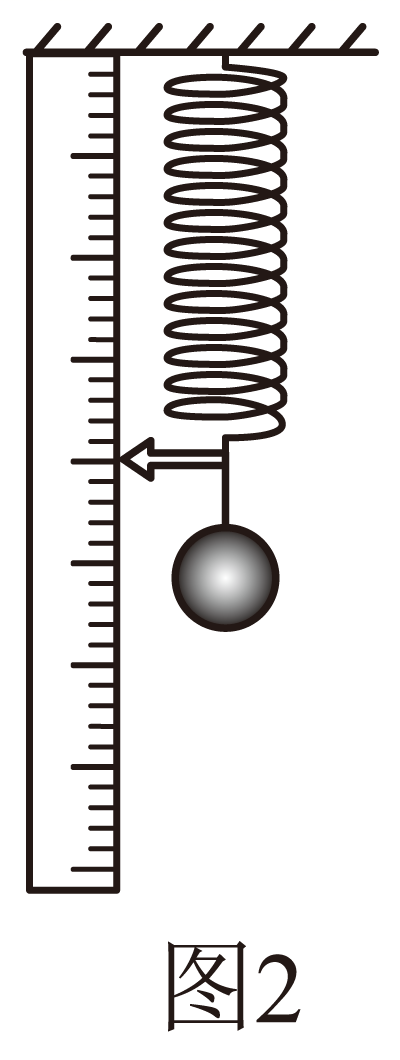
(3) 该同学进一步使用该弹簧、直尺、钢球等制作了一个“竖直加速度测量仪”。如图2所示,不挂钢球时,弹簧下端指针位于直尺20 cm刻度处;下端悬挂钢球,静止时指针位于直尺30 cm刻度处。某次用该装置测量电梯的加速度时,发现弹簧下端指针位于直尺31 cm刻度处,问电梯的加速度方向为(选填“竖直向上”或“竖直向下”),大小为重力加速度g的倍。
- 给溶液命名时,通常把________的名称放在前,
- 我国降水最多和最少的地区分别是( ) A
- 某化学兴趣小组的同学设计了一套实验方案探
- 如图9-6-5所示,一根张紧的水平绳上挂几个摆
- (1)图中使用刻度尺测量物体的长度为
- 选出下列句子中没有错别字的一项。 A.他便
- 上世纪80年代后期人们逐渐认识到,NO在人体
- 关于声现象,下列说法中正确的是( )A
- 七年级(3)班在召开期末总结表彰会之前,班主
- 植物激素对植物的生命活动具有调节作用,赤
- 2009年6月19日,审计署公布了北京奥运会财务
- 设函数,若对任意,都有恒成立。 (1)
- 某地位于东经170°、南纬20°,有关该地的叙述
- 如图,OABC是一张放在平面直角坐标系中的矩形
- (12分)如图,已知△ABC和△DEF是两个边长都
- 跨经度最广的大洋是( ) A.太平洋
- A car needs gas to run and your body also needs food t
- 函数y=-ex的图像( )A.与y=ex的图像关于y轴对
- 在甲、乙、丙、丁四个烧杯中分别加入2.3gNa、
- 面对世界航空制造产业链逐步向中国转移的趋



