探究弹力和弹簧伸长的关系 知识点题库
-
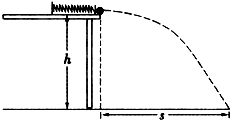
(1) 请你推导出弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式:Ep= .
-
(2) 弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如下表所示:
弹簧的压缩量x (cm)
1.00
1.50
2.00
2.50
3.00
3.50
小钢球飞行的水平距离s (cm)
1.01
1.50
2.01
2.49
3.01
3.50
根据上面的实验数据,请你猜测弹簧的弹性势能Ep与弹簧的压缩量x之间的关系为 .
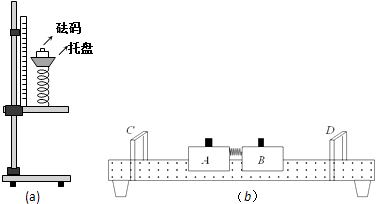
①如图(a),将轻质弹簧下端固定于铁架台,在上端的托盘中依次增加砝码,测得相应的弹簧长度,部分数据如下表:
砝码质量(g) | 50 | 100 | 150 |
弹簧长度(cm) | 8.62 | 7.63 | 6.66 |
②取下弹簧,用天平分别测出滑块A、B的质量(含挡光条)mA、mB;调整气垫导轨,使导轨处于水平,并调整两光电门的间距远大于弹簧的长度.
③在A和B间放入轻弹簧并将弹簧压缩,用电动卡销锁定,记录弹簧的压缩量x;静止放置在气垫导轨上;如图(b)
④释放弹簧,A、B滑块分别在气垫导轨上运动,读出滑块A、B的挡光条分别通过光电门的挡光时间t1和t2 .
-
(1) 由表中数据算得弹簧的劲度系数k=N/m,(g取9.8m/s2)
-
(2) 为了计算被压缩弹簧的弹性势能大小,还必须知道的物理量是,弹簧的弹性势能大小的表达式为EP=.(写出物理量及表示该物理量相应的字母).
钩码个数 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度L/cm | 17.68 | 19.50 | 21.39 | 23.26 | 25.12 |

-
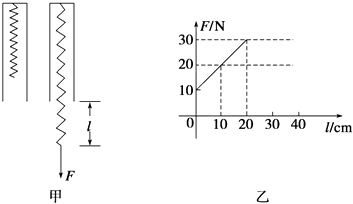
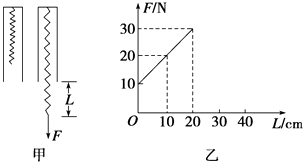
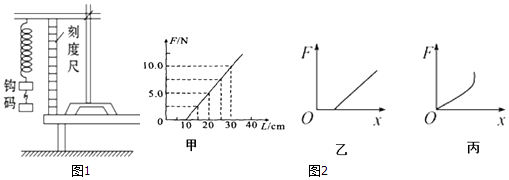
(1) 根据表中数据在图中作出弹簧弹力F与弹簧的长度x图象;
-
(2) 由此图线可得,该弹簧劲度系数k=N/m(结果保留两位有效数字):
-
(3) 图线与x轴的交点表示,其数值L0(填:大于、小于或等于),原因是.
丙图中图线后来弯曲的原因是:;

-
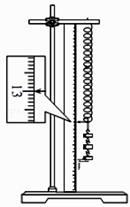
(1) 当在弹簧下端挂上3个钩码时,指针所示位置如图所示,请将上表补充完整.
-
(2) 已知实验所用单个钩码质量为100g,当地重力加速度为9.8m/s2 , 则该弹簧的劲度系数为N/m.(结果保留3位有效数字)

-
(1) 当砝码盘中不加砝码时,指针位置如图乙所示,其示数L0=cm。
-
(2) 在砝码盘中每次增加10g的砝码,并读取相应指针位置的示数L ,以F表示砝码盘内砝码的重力,△L=L-L0为相应弹簧长度的改变量,作出F-ΔL的关系图线如图丙所示。该弹簧的劲度系数为N/m,弹簧的原长为cm。
 重力加速度g取10m/s2 , 结果保留小数点后两位
重力加速度g取10m/s2 , 结果保留小数点后两位 

-
(1) 图(b)中指针对应的刻度尺示数为cm:
-
(2) 在图(c)中将钩码质量为200g时所对应的数据点补上,并做出m﹣l图线;
-
(3) 根据图线算出弹簧的劲度系数为N/m(结果取三位有效数字)。
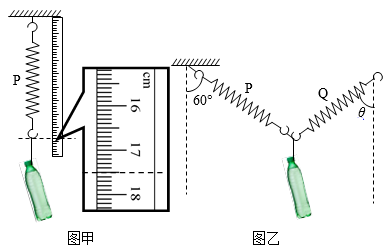
a、将弹簧P上端固定,让其自然下垂,用刻度尺测出此时弹簧P的长度L0=12.50cm;
b、将矿泉水瓶通过细绳连接在弹簧P下端,待矿泉水瓶静止后用刻度尺测出此时弹簧P的长度L1 , 如图甲所示,则L1=cm;
c、在细绳和弹簧Q的挂钩上涂抹少许润滑油,将细绳搭在挂钩上,缓慢的拉起弹簧Q,使弹簧P偏离竖直方向夹角为60°,测出弹簧Q的长度为L2及其轴线与竖直方向夹角为θ,如图乙所示;
⑴取重力加速度g=10m/s2 , 则弹簧P的劲度系数k=;
⑵若要验证力的平行四边形定则,L2和θ需满足的条件是L2=cm,θ=.
⑴将轻质弹簧下端固定于铁架台上,测量弹簧的原长L0;
⑵在弹簧的上端放一托盘,托盘中加适当的砝码,待系统静止时,记录相应的弹簧长度L;
⑶重复步骤(2),记录多组数据如下表所示。
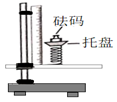
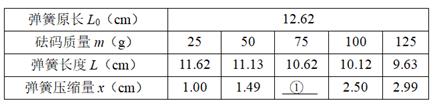
⑷表中①处应填的数据为。由数据可得:弹簧的劲度系数k=N/m,托盘质量m0=g。(g取9.80m/s2)
-
(1) 某同学先把弹簧放在水平桌面上使其自然伸长,用直尺测出弹簧的原长为L0 , 再把弹簧竖直悬挂起来,然后用钩码挂在弹簧下端,测出弹簧的长度为L,把L–L0作为弹簧的伸长量x1 , 改变钩码个数重复操作。由于弹簧自身重力的影响,最后作出的F–x图象,可能是下图中的___________。A .
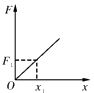 B .
B . 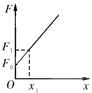 C .
C . 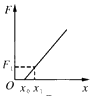 D .
D . 
-
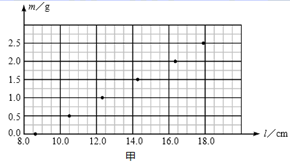
(2) 为了测量某一弹簧的劲度系数,将该弹簧竖直悬挂起来,在自由端挂上不同质量的砝码。实验测出了砝码质量m与弹簧长度l的相应数据,其对应点已在图上标出。
请在图中作出m-L的关系图线。
弹簧的劲度系数为N/m(结果保留3位有效数字)。
-
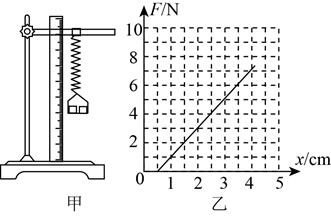
(1) 图像乙不过原点的原因是。
-
(2) 利用图像乙,可求得小盘的重为N,小盘的重力会使弹簧劲度系数的测量结果与真实值相比。(填“变大”、“变小”或“不变”)
-
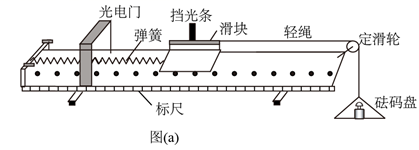
(1) 实验步骤:
①将气垫导轨放在桌面上,打开气泵并将导轨调至水平,判断调平的依据:;
②应选用宽度d=(填“A”、“B”或“C”)的挡光条实验误差更小;
A.0.50cm B.2.00cm C.3.00cm
③将轻质弹簧一端固定于气垫导轨左侧,另一端与滑块相连,当滑块静止(弹簧处于长)时,将光电门中心正对挡光条所在位置安装在导轨上;
④用跨过定滑轮的轻绳将滑块与砝码盘相连,放一个砝码,如图(a)所示。测得稳定时弹簧长度l,计算出弹簧形变量x;
⑤剪断细绳,记录挡光时间t,由v=测得滑块通过光电门时的瞬时速度;
⑥逐次递增砝码个数,重复步骤④⑤。记录的部分数据如下表,根据数据可得弹簧劲度系数k=
N/m(g取9.8m/s2)
砝码质量(g)
0
50
100
150
200
250
弹簧长度l(cm)
15.60
17.56
19.54
21.46
23.40
25.32
⑦根据实验数据,获得
 -x图线,如图(b)所示。
-x图线,如图(b)所示。
-
(2) 回答下列问题:
①释放滑块过程中,弹簧的弹性势能转化为;
②由上述实验可得结论:对同一根弹簧,弹性势能Ep与弹簧形变量x的关系为;
A.
 B.
B.  C.
C. 
简述理由:。
|
钩码个数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
弹力F/N |
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
|
弹簧伸长的长度x/cm |
0 |
2.00 |
3.98 |
6.02 |
7.97 |
9.95 |
11.80 |
13.50 |
-
(1) 根据表中数据在图中作出F-x图线。

-
(2) 根据F-x图线求出图线的斜率为N/m,此斜率与所挂钩码的个数关。(保留2位有效数字)

-
(1) 若某次实验弹簧秤示数如图乙所示,则手的拉力为N;
-
(2) 当手拉力为
 时,刻度尺测量读数为
时,刻度尺测量读数为  ;当手拉力为
;当手拉力为  时,刻度尺测量读数为
时,刻度尺测量读数为  ,则该弹簧秤内弹簧的劲度系数
,则该弹簧秤内弹簧的劲度系数  可表示为;
可表示为;
-
(3) 若实验室有两种规格的弹簧秤,图丙为另一弹簧秤的刻度盘,已知图乙最小分度的长度和图丙最小分度的长度相同,则图乙弹簧的劲度系数
 和图丙弹簧的劲度系数
和图丙弹簧的劲度系数  的关系为
的关系为 
 。
。
-
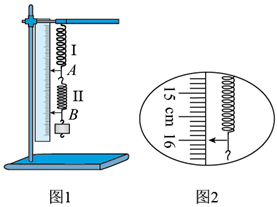
(1) 某次测量如图2,指针示数为cm;
-
(2) 在弹性限度内,将50g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA和LB如下表。用表中数据计算弹簧I的劲度系数k1=N/m,弹簧I的劲度系数k1弹簧II的劲度系数k2(选填“大于”、“等于”或“小于”)(重力加速度g=10m/s2 , 结果保留三位有效数字)。
钩码数
1
2
3
4
LA/cm
15. 71
19. 71
23. 66
27. 76
LB/cm
29. 96
35. 76
41. 51
47. 36
-
(1) 下列操作规范的是____。A . 实验前,应该先把弹簧水平放置测量其原长 B . 逐一增挂钩码,记下每增加一只钩码后指针所指的标尺刻度和对应的钩码总重 C . 随意增减钩码,记下增减钩码后指针所指的标尺刻度和对应的钩码总重 D . 实验结束后,应拆除实验装置,整理并复原实验器材
-
(2) 小明将实验数据记录在表格中。实验时弹力始终未超过弹性限度,
 取
取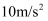 。
。
砝码质量

0
30
60
90
120
150
弹簧总长度
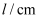
6.0
7.2
8.3
9.5
10.6
11.8
①根据实验数据在坐标纸上作出弹力
 跟弹簧伸长量
跟弹簧伸长量 关系的
关系的 图像。
图像。
②根据
 图像计算弹簧的劲度系数k=
图像计算弹簧的劲度系数k= 。
。
 与所受拉力
与所受拉力 之间的关系图,下列说法中正确的是( )
之间的关系图,下列说法中正确的是( )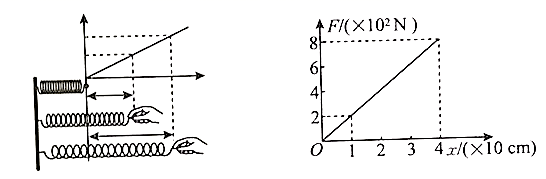
 B . 弹簧的劲度系数是
B . 弹簧的劲度系数是 C . 当弹簧受
C . 当弹簧受 的拉力作用时,弹簧伸长量
的拉力作用时,弹簧伸长量 D . 当弹簧伸长量
D . 当弹簧伸长量 时,弹簧产生的拉力是
时,弹簧产生的拉力是
 ):
):
钩码质量 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
刻度尺的刻度 | 11.60 | 12.41 | 13.22 | 14.01 | 14.79 | 15.60 | 16.41 | 17.21 |
-
(1) 根据所测数据,在答题纸的坐标纸(图乙)上画出弹簧指针所指刻度尺的刻度x与钩码质量m的关系图线。
-
(2) 根据
 图线可计算出,该弹簧的劲度系数为N/m。(结果保留3位有效数字)
图线可计算出,该弹簧的劲度系数为N/m。(结果保留3位有效数字)
- 衡阳是有色金属之乡,水口山铅锌矿历史悠久
- He went ______his way _______some flowers for his mother.A
- 关于声现象,下列说法正确的是 A.只要物体
- 2010年1月18,国家信息中心发布的《西部大开
- 读图获取信息,完成1〜2题。 1.图中数码表
- 夏天,把一大块冰放在塑料袋中,塑料袋没有
- 填空:(每空1分,共5分) ①宁国府贾珍的儿
- (2010巢湖)右图中的牛没有“吹牛”,它的
- 如图所示,竖直放置的轻弹簧一端固定在地面
- 一定量的铁与一定量的浓HNO3反应,得到硝酸
- 由短周期非金属元素X和元素Y组成的化合物Y2X3
- 阅读下面的文字,完成下列小题。 自先秦到
- 1438年,发表于德意志地区的《皇帝西基斯蒙
- (1)写出电解饱和食盐水的离子方程式
- This is an old English saying. Have you heard it before?
- 下列根据化学方程式的计算题有错误,简述错
- 阅读下面的文字,完成下列小题。 田雪原:
- 在探究“菜青虫的取食行为”时,需要从菜青
- 稀土有工业“黄金”之称,它是很多高精尖产
- 如图所示实验操作或装置正确的是( ) A.




