直线与圆的位置关系 知识点题库
已知圆的半径为6.5cm,圆心到直线l的距离为4.5cm,那么这条直线和这个圆的公共点的个数是( ).
A . 0
B . 1
C . 2
D . 不能确定
如图,在直角坐标系中,⊙O的半径为1,则直线y=﹣x+ 与⊙O的位置关系是( ).
与⊙O的位置关系是( ).

A . 相离
B . 相交
C . 相切
D . 以上三种情形都有可能
若∠OAB=30°,OA=10cm,则以O为圆心,6cm为半径的圆与直线AB的位置关系是( )
A . 相交
B . 相切
C . 相离
D . 不能确定
在平面直角坐标系中,抛物线y=-(x-2)2+1的顶点是点P,对称轴与x轴相交于点Q,以点P为圆心,PQ长为半径画⊙P,那么下列判断正确的是( )
A . x轴与⊙P相离;
B . x轴与⊙P相切;
C . y轴与⊙P与相切;
D . y轴与⊙P相交.
如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是 .

在Rt△ABC中,AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,那么半径r的取值范围是 .
如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=  ,则弧BN的长为.
,则弧BN的长为.
 ,则弧BN的长为.
,则弧BN的长为. 
在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( )
A . 与x轴相离,与y轴相切
B . 与x轴,y轴都相离
C . 与x轴相切,与y轴相离
D . 与x轴,y轴都相切
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.

-
(1) 试判断线段AB与AC的数量关系,并说明理由;
-
(2) 若PC=2
 ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
-
(3) 若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
⊙O直径为8cm,有M、N、P三点,OM=4cm,ON=8cm,OP=2cm,则M点在,N点在圆,P点在圆。
已知⊙O的半径为10cm,弦MN∥E,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为( )cm.
A . 14或2
B . 14
C . 2
D . 6
如图,以点P为圆心作圆,所得的圆与直线l相切的是( )

A . 以PA为半径的圆
B . 以PB为半径的圆
C . 以PC为半径的圆
D . 以PD为半径的圆
平面直角坐标系中,⊙P的圆心坐标为(-4,-5),半径为5,那么⊙P与y轴的位置关系是( )
A . 相交
B . 相离
C . 相切
D . 以上都不是
在平面直角坐标系  中,对于半径为
中,对于半径为  的
的  和点
和点  ,给出如下定义:
,给出如下定义:
 中,对于半径为
中,对于半径为  的
的  和点
和点  ,给出如下定义:
,给出如下定义: 若  ,则称
,则称  为
为  的“近外点”.
的“近外点”.


-
(1) 当
 的半径为2时,点
的半径为2时,点  ,
,  ,
,  ,
,  中,
中,  的“近外点”是;
的“近外点”是;
-
(2) 若点
 是
是  的“近外点”,求
的“近外点”,求  的半径
的半径  的取值范围;
的取值范围;
-
(3) 当
 的半径为2时,直线
的半径为2时,直线  与
与  轴交于点
轴交于点  ,与
,与  轴交于点
轴交于点  ,若线段
,若线段  上存在
上存在  的“近外点”,直接写出
的“近外点”,直接写出  的取值范围.
的取值范围.
如图,已知直线  与x轴、y轴分别交于B,C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是( )
与x轴、y轴分别交于B,C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是( )
 与x轴、y轴分别交于B,C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是( )
与x轴、y轴分别交于B,C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是( ) 
A . 30
B . 29
C . 28
D . 27
半径为10的⊙O和直线l上一点A,且OA=10,则直线l与⊙O的位置关系是( )
A . 相切
B . 相交
C . 相离
D . 相切或相交
如图,已知⊙O是以数轴上原点O为圆心,半径为2的圆,∠AOB=45°,点P在x正半轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P点对应的数为x,则x的取值范围是.

如图,以点P为圆心,以下列选项中的线段的长为半径作圆,所得的圆与直线l相切的是( )

A . PA
B . PB
C . PC
D . PD
在  中,
中,  ,
,  ,
,  ,点
,点  ,点
,点  同时从点
同时从点  出发,点
出发,点  沿边
沿边  以
以  的速度向点
的速度向点  运动,点
运动,点  从点
从点  出发,沿边
出发,沿边  以
以  的速度向点
的速度向点  运动(点
运动(点  不与
不与  ,
,  重合,点
重合,点  不与
不与  ,
,  重合),设运动时间为
重合),设运动时间为  .
.
 中,
中,  ,
,  ,
,  ,点
,点  ,点
,点  同时从点
同时从点  出发,点
出发,点  沿边
沿边  以
以  的速度向点
的速度向点  运动,点
运动,点  从点
从点  出发,沿边
出发,沿边  以
以  的速度向点
的速度向点  运动(点
运动(点  不与
不与  ,
,  重合,点
重合,点  不与
不与  ,
,  重合),设运动时间为
重合),设运动时间为  .
.

-
(1) 求证:
 ;
;
-
(2) 当
 为何值时,以
为何值时,以  为直径的
为直径的  与直线
与直线  相切?
相切?
-
(3) 把
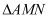 沿直线
沿直线  折叠得到
折叠得到  ,若
,若  与梯形
与梯形  重叠部分的面积为
重叠部分的面积为  ,试求
,试求  关于
关于  的函数表达式,并求
的函数表达式,并求  为何值时,
为何值时,  的值最大,最大值是多少?
的值最大,最大值是多少?
如图,在每个小正方形的边长为1的网格中, 的顶点A、B、C均落在格点上.
的顶点A、B、C均落在格点上.
 的顶点A、B、C均落在格点上.
的顶点A、B、C均落在格点上.
-
(1)
 的周长为.
的周长为.
-
(2) 请在如图所示的网格中,用无刻度的直尺在AC上确定一点M,使以点M为圆心,以MC为半径的
 与AB相切,并简要说明点M的位置是如何找到的(不要求证明): ▲ .
与AB相切,并简要说明点M的位置是如何找到的(不要求证明): ▲ .
最近更新
- 在下列几种运动中,机械能一定不守恒的是()A. 质点做匀速圆周运动B. 物体做匀速直线运动C. 物体做匀变速运动D. 打
- 《芦花荡》一文是 (作者)的“白洋淀纪事之二”,“之一”是他的另一篇小说《 》。
- 《中共中央关于加强和改进新形势下党的建设若干重大问题的决定》指出,要加强网络舆情分析,健全反腐倡廉网络举报和受理机制、网
- 细胞内与遗传有关的物质,从复杂到简单的结构层次是 A.脱氧核苷酸→基因→DNA→染色体 B.染色体→脱氧核苷酸→D
- 解不等式组,并把它的解集在数轴上表示出来。
- 显微镜是生物学实验常用的观察工具,下列相关的实验操作中不正确的是 A.设法提高细胞环境温度,有利于在显微镜下观察到植物细
- 右图中X、Y、Z是初中化学常见物质,箭头表示物质之间可以向箭头方向一步转化,下列说法中不正确的是 A.若X是SO
- 医学界通过14C标记的C60发现一种C60的羧酸衍生物,在特定条件下可以通过断裂DNA抑制艾滋病病毒的繁殖,则14C的用
- People believes that climbing can do good tohealth. Where ca
- 实验室里保存下列试剂的方法,有错误的是 A.新制氯水盛放在棕色试剂瓶中,存放于低温避光的地方 B.液溴易挥发,盛放在用水
- 的值为() A.- B. C.
- 图12-12所示为t=0时刻的一列简谐横波的部分波形图象,波的传播速度是4.0 m/s,在该时刻质点a的速度方向是向下的
- 癌症是严重威胁人类健康的疾病之一。引起细胞癌变的内在因素是() A.细胞中酪氨酸酶活性降低 B.致癌因子激活原癌基因 C
- 2008年,宁夏自治区成立50周年。50年来,宁夏自治区发生了翻天覆地的变化,充分体现出民族区域自治制度的优越性。民族区
- 已知函数f(x)为奇函数,且当x>0时,f(x)=x2+,则f(-1)=() A.-2
- 下列物质中,既含有离子键又含有非极性键的是 A.CO2 B
- 下列变化过程中,有白烟产生的() A.硫在空气中燃烧 B.打开盛有浓盐酸的瓶盖 C.铁丝在氧气中燃烧 D.红磷在空气
- 英、德、法、意等美国盟友,不顾美国反对,加入了由中国倡议筹建的具有广阔发展前景的亚洲基础设施投资银行。由此可见 A、独立
- “化疗”是控制癌细胞生长的方法之一,药物可以杀死癌细胞,图中给出的是一个典型的化疗过程,每3周给药1次(图中箭头所示)
- 如图,A、B两物体质量都是m,A放在台秤上,若轻绳和滑轮之间的摩擦不计,则台秤读数N和悬点O所受的拉力T,其可能值为(



