直线与圆的位置关系 知识点题库
如图,在直角坐标系中,⊙O的半径为1,则直线 与⊙O的位置关系是( )
与⊙O的位置关系是( )

A . 相离
B . 相交
C . 相切
D . 无法确定
已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A . 相离
B . 相切
C . 相交
D . 无法判断
如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、 为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第 秒.
为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第 秒.
 为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第 秒.
为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第 秒.
如图:半径为2的圆心P在直线y=2x﹣1上运动,当⊙P与x轴相切时圆心P的坐标为.

如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y=  (x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2
(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2 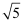 时,点P的坐标为( )
时,点P的坐标为( )
 (x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2
(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2 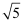 时,点P的坐标为( )
时,点P的坐标为( ) 
A . (1,6)和(6,1)
B . (2,3)和(3,2)
C . (  ,3
,3  )和(3
)和(3  ,
,  )
D . (
)
D . (  ,2
,2  )和(2
)和(2  ,
,  )
)
 ,3
,3  )和(3
)和(3  ,
,  )
D . (
)
D . (  ,2
,2  )和(2
)和(2  ,
,  )
)
已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A . 相离
B . 相切
C . 相交
D . 无法判断
如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )

A . 30°
B . 45°
C . 60°
D . 90°
如果我们把太阳看作一个圆,把地平线看作一条直线,太阳在升起离开地平线后,太阳和地平线的位置关系是.
已知圆O的圆心到直线L的距离为3,若圆上有且只有2个点到L的距离为2,则半径r的取值范围是( )
A . r=3
B . 1<r<3
C . 1<r<5
D . 1≤r≤5
如图1,直线y=﹣  x+8,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP,连结PQ,设点P的坐标为P(0,t).
x+8,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP,连结PQ,设点P的坐标为P(0,t).
 x+8,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP,连结PQ,设点P的坐标为P(0,t).
x+8,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP,连结PQ,设点P的坐标为P(0,t). 
-
(1) 求点B的坐标.
-
(2) 若t=1时,连接BQ,求△ABQ的面积.
-
(3) 如图2,以PQ为直径作⊙I,记⊙I与射线AC的另一个交点为E.

①若
 =
=  ,求此时t的值.
,求此时t的值.
若等边三角形ABC的边长为  cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是.
cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是.
 cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是.
cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是.
已知⊙O的直径是5cm,点O到同一平面内直线l的距离5cm,则直线l与⊙O的位置关系是 ( )
A . 相离
B . 相切
C . 相交
D . 无法确定
已知⊙O的半径为4,点O到直线m的距离为d,若直线m与⊙O公共点的个数为2个,则d可取( )
A . 5
B . 4.5
C . 4
D . 0
⊙O的直径为7,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A . 相离
B . 相切
C . 相交
D . 相切或相交
如图,已知⊙O是以数轴原点O为圆心,半径为1的圆,  ,点P在数轴上运动,若过点P且与
,点P在数轴上运动,若过点P且与  平行的直线与⊙O有公共点,设
平行的直线与⊙O有公共点,设  ,则x的取值范围是( )
,则x的取值范围是( )
 ,点P在数轴上运动,若过点P且与
,点P在数轴上运动,若过点P且与  平行的直线与⊙O有公共点,设
平行的直线与⊙O有公共点,设  ,则x的取值范围是( )
,则x的取值范围是( ) 
A .  ≤
≤  ≤
≤  B .
B . 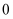 ≤
≤  ≤
≤  C .
C .  ≤
≤  ≤
≤  D .
D .  >
> 
 ≤
≤  ≤
≤  B .
B . 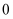 ≤
≤  ≤
≤  C .
C .  ≤
≤  ≤
≤  D .
D .  >
> 
如图:在平面直角坐标系  中,点
中,点  .
.
 中,点
中,点  .
. 
-
(1) 尺规作图:求作过
 三点的圆;
三点的圆;
-
(2) 设过
 三点的圆的圆心为M,利用网格,求点M的坐标;
三点的圆的圆心为M,利用网格,求点M的坐标;
-
(3) 若直线
 与
与  相交,直接写出a的取值范围.
相交,直接写出a的取值范围.
已知⊙O的半径为  ,圆心O到直线L的距离为
,圆心O到直线L的距离为  ,则直线L与⊙O的位置关系是.
,则直线L与⊙O的位置关系是.
 ,圆心O到直线L的距离为
,圆心O到直线L的距离为  ,则直线L与⊙O的位置关系是.
,则直线L与⊙O的位置关系是.
已知  的圆心O到直线l的距离为5,
的圆心O到直线l的距离为5,  的半径为3,则直线l和
的半径为3,则直线l和  的位置关系为( )
的位置关系为( )
 的圆心O到直线l的距离为5,
的圆心O到直线l的距离为5,  的半径为3,则直线l和
的半径为3,则直线l和  的位置关系为( )
的位置关系为( )
A . 相离
B . 相切
C . 相交
D . 相交或相切
如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若  ,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.
,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.
 ,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.
,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由. 
我们规定:在平面直角坐标系  中,如果点P到原点O的距离为
中,如果点P到原点O的距离为  ,点M到点P的距离是a的整数倍,那么点M就是点P的k倍关联点.
,点M到点P的距离是a的整数倍,那么点M就是点P的k倍关联点.
 中,如果点P到原点O的距离为
中,如果点P到原点O的距离为  ,点M到点P的距离是a的整数倍,那么点M就是点P的k倍关联点.
,点M到点P的距离是a的整数倍,那么点M就是点P的k倍关联点. 
-
(1) 当点
 的坐标为
的坐标为  时,
时, ①如果点
 的2倍关联点M在x轴上,那么点M的坐标是;
的2倍关联点M在x轴上,那么点M的坐标是;②如果点
 是点
是点  的k倍关联点,且满足
的k倍关联点,且满足  ,
,  .那么k的最大值为;
.那么k的最大值为; -
(2) 如果点
 的坐标为
的坐标为  ,且在函数
,且在函数  的图象上存在
的图象上存在  的2倍关联点,求b的取值范围.
的2倍关联点,求b的取值范围.
最近更新
- 下列物品所使用的主要材料属于合成材料的是 ( ) A.玻璃水杯
- 阅读下面的文字,完成下列各题。马云的大时代章 苒1982年,陕西作家路遥的小说《人生》在《收获》上发表。有个瘦小的年轻人
- 下列物质属于混合物的是()A. 锌 B. 可燃冰 C. 双氧水 D. 硝酸铵
- 下列实例中,目的是为了增大压强的是: A.刀刃做得很薄 B.书包带做得较宽 C.
- 将下列各种液体分别与溴水混合并振荡,静置后混合液分成两层,下层几乎呈无色的是 A.苯
- 下列物质水溶液遇石蕊呈蓝色的是() A.氯化铵 B.醋酸 C.纯碱 D.食盐
- 遗传的基本规律指的是某物质在遗传过程中的传递规律,这种物质是 A.性状 B.遗传物质 C.基因
- 定义在上的函数是减函数,且是奇函数,若,求实数的范围。
- 锂离子电池的应用很广,其正极材料可再生利用。某锂离子电池正极材料有钴酸锂(LiCoO2)、导电剂乙炔黑和铝箔等。充电时,
- 甲、乙、丙、丁四种物质中,甲、乙、丙均含有相同的某种元素,它们之间具有如下转化关系:。下列有关物质的推断不正确的是
- 19世纪,工业革命推动了欧美资产阶级代议制的进一步发展。下列各项中,体现了这一进步趋势的是 A英国责任内阁制的形成
- 我国由于冷锋活动而出现的天气有 ①北方夏季的暴雨 ②沿海地区的台风 ③冬季爆发的寒潮 ④冬、春季节的大风、沙尘暴 A
- 120℃时,1体积某烃和4体积O2混合,完全燃烧后恢复到原来的温度和压强,体积不变,该烃分子式中所含碳原子数不可能是(
- 除去氯气中含有的少量水蒸气,所用试剂正确的是 A.固体氢氧化钠
- 20世纪70年代以来,我国实行人口基本国策的根本原因是 A.人口分布不均匀 B.人口增长与
- 下列溶液肯定是酸性的是: ( )A. 含 H+的
- 在的展开式中,常数项是 。
- 下列关于Na2CO3、NaHCO3的性质比较中,不正确的是( ) A.热稳定性:Na2CO3>NaHCO3
- 下列表示物质结构的化学用语或模型正确的是A.8个中子的碳原子的核素符号:12C B.HF的电子式:C.Cl-离子的
- 2010年广州亚运会吉祥物设计者将形象运动时尚的五只羊,分别取名“阿祥”、“阿和”、“阿如”、“阿意”、“乐羊羊”,组成



