高中 物理


-
(1) 由以上信息,可知a点(选填“是”或“不是”)小球的抛出点;
-
(2) 由以上信息,可以推算出该星球表面的重力加速度为m/s2;
-
(3) 由以上信息可以算出小球平抛的初速度是m/s;
-
(4) 由以上信息可以算出小球在b点时的速度是m/s.
 的绝缘轻绳悬挂一个带电小球,所带电荷量
的绝缘轻绳悬挂一个带电小球,所带电荷量  .现加一方向水平且区域足够大的匀强电场,小球稳定后悬线偏离竖直方向的夹角为
.现加一方向水平且区域足够大的匀强电场,小球稳定后悬线偏离竖直方向的夹角为 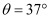 ,重力加速度
,重力加速度  取
取  ,已知
,已知  。若将轻绳向右拉至水平后由静止释放,不计空气阻力,则小球到达最低点时的速度大小为( )
。若将轻绳向右拉至水平后由静止释放,不计空气阻力,则小球到达最低点时的速度大小为( ) 
 B .
B .  C .
C .  D .
D . 

-
(1) 小球在B点时的速度大小;
-
(2) 小球在B点时半圆轨道对它的弹力大小;
-
(3) 小球在A点时对半圆轨道的压力大小。
-
(1) 推导第一宇宙速度v1的表达式;
-
(2) 一卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h。求卫星的运行周期T。
-
(1) 由于电流表量程偏小,该同学首先需将电流表改装成量程为0~4.0V的电压表,则应将电流表与电阻箱R1(选填“串联”或“并联”),并将该电阻箱阻值调为Ω;

-
(2) 接着该同学用改装的电压表对电池的电动势及内阻进行测量,实验电路如图所示,通过改变电阻R2测相应的电压U,且作相关计算后一并记录如下表:
1
2
3
4
5
6
R2(Ω)
50.0
30.0
20.0
15.0
12.0
10.0
U(V)
2.89
2.85
2.81
2.77
2.72
2.68
 (mA)
(mA)57.8
95.0
141
185
227
268

①根据表中数据,在坐标纸上进行描点,并画
 图线;
图线;②根据图线可得电池的电动势E是V,内阻r是Ω(结果保留两位小数)。
 =10kg的滑块在与水平方向成
=10kg的滑块在与水平方向成  =37°的恒力
=37°的恒力  作用下,从A点由静止开始运动,前进到B点后撤掉力
作用下,从A点由静止开始运动,前进到B点后撤掉力  。小物块继续前进经过C点进入半圆轨道,恰能通过最高点D。若恒力
。小物块继续前进经过C点进入半圆轨道,恰能通过最高点D。若恒力  大小为100N,且AC段长为10.5m ,动摩擦因数为μ=0.2。求:
大小为100N,且AC段长为10.5m ,动摩擦因数为μ=0.2。求: 
-
(1) D点速度大小?
-
(2) AB间的距离
 为多少?(sin37°=0.6,g=10m/s2)
为多少?(sin37°=0.6,g=10m/s2)

质量为40kg的物体在水平面上运动,图中两直线分别表示物体受水平拉力和不受水平拉力时的速度一时间图象,则下列说法正确的是( )
 B . 物体不受水平拉力时的速度—时间图象一定是
B . 物体不受水平拉力时的速度—时间图象一定是 C . 物体所受摩擦力一定等于40 N
D . 水平拉力一定等于80N
C . 物体所受摩擦力一定等于40 N
D . 水平拉力一定等于80N

如图甲所示,在匀强磁场中,一矩形金属线圈两次分别以不同的转速绕与磁感线垂直的轴匀速转动,产生的交变电动势图象如图乙中曲线a、b所示,则( )

A.两次t=0时刻线圈的磁通量均为零
B.曲线a、b对应的线圈转速之比为3:2
C.曲线a表示的交变电动势频率为25 Hz
D.曲线b表示的交变电动势有效值为10 V
如图所示,三只灯泡均正常发光,现将滑动变阻器R的滑片向下移动,已知原线圈上的电压及原、副线圈的匝数均不变,则下列说法中正确的是( )

A. 灯L3变暗
B. 灯L1和L2均变暗
C. 变压器原线圈的输入功率变大
D. 副线圈n2中的电流变大
如下图所示,A、B、C三个物体叠放在桌面上,在A的上面加上一个作用力F,则物体C受力的个数是

A.1个 B.2个
C.3个 D.4个
有一待测的电阻器Rx,其阻值约在40~50Ω之间,实验室准备用来测量该电阻值的实验器材有:
电压表V(量程0~10 V,内电阻约20 kΩ) ;
电流表A1,(量程0~500 mA,内电阻约20Ω);
电流表A2,(量程0~300 mA,内电阻约4Ω) ;
滑动变阻器R1,(最大阻值为10Ω,额定电流为2 A) ;
滑动变阻器R2(最大阻值为250Ω,额定电流为0.1 A);
直流电源E(电动势为9V,内电阻约为0. 5Ω);
开关及若干导线.
实验要求电表读数从零开始变化,并能多测出几组电流、电压值,以便画出I-U图线.
①电流表应选用 .
②滑动变阻器选用 (选填器材代号)).
竖直升空的火箭,其v﹣t图象如图所示,由图可知以下说法中正确的是( )
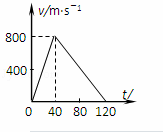
A. 火箭上升的最大高度为16000m
B. 火箭上升的最大高度为48000m
C. 火箭经过120s落回地面
D. 火箭上升过程中的加速度始终是20m/s2
关于电磁感应现象,下列说法中正确的是( )
A.只要有磁通量穿过电路,电路中就有感应电流
B.只要闭合电路在做切割磁感线运动,电路中就有感应电流
C.只要穿过闭合电路的磁通量足够大,电路中就有可能产生感应电流
D.只要穿过闭合电路的磁通量发生变化,电路中就一定有感应电流
电动势为E、内阻为r的电池与定值电阻R0、变阻器R串联,如图所示,设R0=r,Rab=2r,当变阻器的滑片自a端向b端滑动时,下列各物理量中随之减小的是( )

A. 电池的输出功率 B. 变阻器消耗的功率
C. 固定电阻R0消耗的功率 D. 电池内阻消耗的功率

(1)已知滑块与车面间动摩擦因数μ=0.2,滑块质量m=1kg,车长L=2m,车速v0=4m/s,取g=10m/s2,当滑块放到车面中点的同时对该滑块施加一个与车运动方向相同的恒力F,要保证滑块不能从车的左端掉下,恒力F大小应该满足什么条件?
(2)在(2)的情况下,力F取最小值,要保证滑块不从车上掉下,力F的作用时间应该在什么范围内?
- ---- ______ did you stay in Tibet? ----For only a week.A.
- 物体A的质量m1=1 kg,静止在光滑水平面上的木板B的质量为m2=0.5 kg、长l=1 m,某时刻A以v0=4 m/
- .根据下列材料及漫画“危险”(图11)提供的信息,完成下列各题。 2010年3月19日-21日,我国经历了一场大范
- ---You are a goodboy! ---_______________. A. No, I’mnot
- 下列语段中画横线的词语,使用不恰当的一项是( ) 哈佛大学教授杜维明说,“西方的人文学和人文主义基本上是反自然和
- 函数y=的自变量x取值范围是_____.
- Seeing with Sound According to a British news report,some b
- 如图5-6所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端
- 在相同条件下,下列各组气体中,分子数一定相同的是A.34g NH3和4g H2
- 下列各组词语中没有错别字的一组是 A.纪元 窖藏 教课书 精雕细
- 下列植物属于双子叶植物的是( ) A.黄瓜 B.小麦 C.玉米 D.郁金香
- 对生物膜的认识不正确的是( ) A.哺乳动物成熟红细胞除细胞膜外,无其它生物膜 B.细胞膜上蛋白质分子有两类,其中一类
- 阅读下面的文言文,完成后面题目。 苏轼传 熙宁四年,会上元敕府市浙灯,且令损价。轼疏言:“陛下岂以灯为悦?此不过以奉二宫
- 下列根据元素周期律做出的推断正确的是 A、Na、Mg、Al的还原性依次增强 B、HF、HCl、HBr的稳定性依次增强 C
- 某芳香族化合物A的水溶液呈酸性,测得A分子中无酚羟基。A可发生下图所示转化,其中F为五元环状化合物;G可使溴的四氯化碳溶
- 某矿石由前20号元素中的4种组成,其化学式为WYZX4。X、Y、Z、W分布在三个周期,原子序数依次增大,W、Y为金属元素
- 根据圣彼得堡6月22日太阳高度随时间变化曲线图,回答当圣彼得堡6月22日正午时,南极长城站的区时为
- 某同学加热氯酸钾制氧气,错把高锰酸钾当作二氧化锰放入氯酸钾内,其结果与只加热氯酸钾相比() A.反应速率不变 B.生成氧
- A person may have a false idea about himself that will stop
- 下列各组单质中,前者能将后者从化合物中置换出来的是 ( ) ①Al、Fe ②C、Si ③Mg、



