高中 物理
-
(1) A车若仍按原速前进,两车是否会相撞?若会相撞,将在B刹车后多长时间相撞?
-
(2) 若B车在刹车的同时发出信号,使A车收接到信号立即加速前进,若不计发射和接收信号的
时间差,则A车的加速度至少是多大时,才能避免事故发生?(为了计算方便,可能用到的数据有
 =1.4,
=1.4,  =1.7,
=1.7,  =2.4)
=2.4)

 →
→  +x变反应制成核电池,已知
+x变反应制成核电池,已知  的半衰期约为2.6年,
的半衰期约为2.6年,  、
、  原子核及x粒子的质量分别为m1、m2、m,真空中的光速为c,则( )
原子核及x粒子的质量分别为m1、m2、m,真空中的光速为c,则( )
 B . 5.2年后所有
B . 5.2年后所有  原子核均已衰变
C . 每个
原子核均已衰变
C . 每个  原子核衰变放出的能量为(m1-m2-m)c2
D . 单位时间内该电池因衰变而放出的核能一直保持不变
原子核衰变放出的能量为(m1-m2-m)c2
D . 单位时间内该电池因衰变而放出的核能一直保持不变




 、电阻不计的平行光滑金属导轨水平放置,一端与阻值
、电阻不计的平行光滑金属导轨水平放置,一端与阻值  的电阻相连,导轨间存在
的电阻相连,导轨间存在  、方向垂直导轨平面匀强磁场,一根质量
、方向垂直导轨平面匀强磁场,一根质量 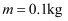 、电阻
、电阻  的金属棒置于导轨上,并与导轨垂直金属棒在外力F作用下以速度
的金属棒置于导轨上,并与导轨垂直金属棒在外力F作用下以速度  沿导轨向右匀速运动,求:
沿导轨向右匀速运动,求: 
-
(1) 金属棒在磁场中运动时产生的感应电动势的大小;
-
(2) 通过金属棒的电流大小及方向;
-
(3) 外力F的大小。
 ,摆球的直径为
,摆球的直径为  ,然后用秒表记录了单摆完成50次全振动所用的时间,则
,然后用秒表记录了单摆完成50次全振动所用的时间,则
-
(1) 该单摆的摆长为cm
-
(2) 如果测出的g值偏小,可能的原因是______A . 测量摆线长,线拉得过紧 B . 摆线上端没有固定,振动中出现松动,使摆线变长了 C . 开始计时时,秒表按下迟了 D . 实验中误将49次全振动记为50次
-
(3) 该同学由测量数据作出
 图线,根据图线求出重力加速度
图线,根据图线求出重力加速度 
 (保留3位有效数字)。
(保留3位有效数字)。 
-
(1) 求该飞机在起飞过程中的加速度大小;
-
(2) 求该飞机在起飞过程中的平均阻力大小.

如图甲所示,圆形线圈与两平行金属板相连接(板间距足够大),线圈中存在垂直于纸面的匀强磁场,其磁感应强度B随时间变化的关系如图乙所示,规定磁场方向向里为正方向,在平行金属板之间固定一带正电的粒子,则( )

 时刻,粒子受到向上的洛伦兹力
B . 在t=
时刻,粒子受到向上的洛伦兹力
B . 在t=  时刻,粒子受到向下的电场力
C . 在t=
时刻,粒子受到向下的电场力
C . 在t= 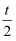 时刻,粒子不受电场力
D . 粒子在t=
时刻,粒子不受电场力
D . 粒子在t=  和t=
和t=  时刻,受到的电场力方向相反
时刻,受到的电场力方向相反

 D . 转台的角速度一定满足:
D . 转台的角速度一定满足:
如图所示,小车 A 通过一根绕过定滑轮的轻绳吊起一重物 B ,开始时用力按住 A 使 A 不动,现设法使 A 以速度 向左做匀速直线运动,某时刻连接 A 车右端的轻绳与水平方向成


A .当轻绳与水平方向成 θ 角时重物 B 的速度
B .当轻绳与水平方向成 θ 角时重物 B 的速度 
C . B 上升到滑轮处前的过程中处于失重状态
D . B 上升到滑轮处前的过程中处于超重状态
如图所示,在带负电荷的橡胶圆盘附近悬挂一个小磁针。现驱动圆盘绕中心轴高速旋转,小磁针发生偏转。下列说法正确的是( )

A.偏转原因是圆盘周围存在电场
B.偏转原因是圆盘周围产生了磁场
C.仅改变圆盘的转动方向,偏转方向不变
D.仅改变圆盘所带电荷的电性,偏转方向不变
如图所示电路中,电源电动势ε=50V,内阻r=5Ω,电阻R1=R2=30Ω。若再接入一个电阻R3,电压表示数为40V,不计电压表对电路的影响,问:R3应接在什么位置上?(画出电路图表示)R3的阻值多大?

已知地球的质量是月球质量的 81 倍,地球半径大约是月球半径的 4 倍,不考虑地球、月球自转的影响,以上数据可推算出 ( )
A . 地球表面的重力加速度与月球表面重力加速度之比为 9:16
B . 地球的平均密度与月球的平均密度之比为 9:8
C . 靠近地球表面沿圆轨道运动的航天器的周期与靠近月球表面沿圆轨道运行的航天器的周期之比约为 8:9
D . 靠近地球表面沿圆轨道运行的航天器的线速度与靠近月球表面沿圆轨道运行的航天器的线速度之比约为 81:4
如图所示,质量均为 m 的物体 B 、 C 分别与轻质弹簧的两端相栓接,将它们放在倾角为![]() 的光滑斜面上,静止时弹簧的形变量为
的光滑斜面上,静止时弹簧的形变量为![]() .斜面底端有固定挡板 D,物体 C 靠在挡板 D 上.将质量也为 m 的物体 A 从斜面上的某点由静止释放,A 与 B 相碰.已知重力加速度为 g,弹簧始终处于弹性限度内,不计空气阻力.求:
.斜面底端有固定挡板 D,物体 C 靠在挡板 D 上.将质量也为 m 的物体 A 从斜面上的某点由静止释放,A 与 B 相碰.已知重力加速度为 g,弹簧始终处于弹性限度内,不计空气阻力.求:

(1)弹簧的劲度系数 k;
(2)若 A 与 B 相碰后粘连在一起开始做简谐运动,当 A 与 B 第一次运动到最高点时,C 对挡板 D 的压力恰好为零,求 C 对挡板 D 压力的最大值;
(3)求(2)情况下,A由静止释放的点与A、B相碰点间的距离?
如图甲、乙、丙所示,边长为a的等边三角形区域内有匀强磁场,磁感应强度B的方向垂直纸面向外。边长为a的等边三角形导体框架EFG,在![]() 时恰好与磁场区域的边界重合,而后以周期T绕其中心沿顺时针方向匀速旋转,于是在框架EFG中有感应电流。规定电流按E→F→G→E方向流动时电流强度取正,反向流动时取负。设框架EFG的总电阻为R,则从
时恰好与磁场区域的边界重合,而后以周期T绕其中心沿顺时针方向匀速旋转,于是在框架EFG中有感应电流。规定电流按E→F→G→E方向流动时电流强度取正,反向流动时取负。设框架EFG的总电阻为R,则从![]() 到
到![]() 时间内平均电流强度I1=_______;从
时间内平均电流强度I1=_______;从![]() 到
到![]() 时间内平均电流强度I2=_______。
时间内平均电流强度I2=_______。

下图描绘一定质量的氧气分子分别在0℃和100℃两种情况下速率分布情况,符合统计规律的是( )

- 下列实验操作中正确的是( )
- 下列分子属于手性分子的是()
- 下列各分子中,是极性分子的为( )A.BeCl2 B.BF3
- 图11漫画《今日武松》体现的哲理是 A.实践是认识的目的 B.能指导人们行动的价值观才是正确的 C.自然规律不
- 贫血的原因是( ) A、红细胞的数量过少 B、血红蛋白含量过少 C、血小板数量过少
- 回答下列问题: 我国是人民民主专政的社会主义国家 (1)请运用政治常识,在表格材料下方相应的空栏内,填写我国公民政治参与
- (江苏省南京市2010届高三第二次模拟考试)武汉起源于军事要塞,后来城市功能转变为以商贸为主,目前构建了“城市圈—都市发
- 下列溶液一定呈中性的是 () A.pH=7的溶液 B.c(H+)=c(OH-)的溶液 C.由强酸
- The girl arranged to have piano lessons at the training cent
- 右图出自《天工开物》。这一组图反映了中国古代农业生产的什么特点?(注:耙:碎土、平地;耔:培土) ①农事精耕细作 ②农
- ......
- I was talking Eric the phone at
- 如图3所示,单摆摆球为带正电的玻璃球,摆长为且不导电,悬挂于点.当摆球摆过竖直线时便进入或离开一匀强磁场,此磁场的方向与
- 19.根据以下材料,选取角度,自拟题目,写一篇不少于800字的文章;文体不限,诗歌除外。 小雨点从天空往下飞,它看到下方
- 下列各项中符合现代生物进化理论观点的是 ( ) A.绵羊和山羊之间不能进行基因交流 B.东北虎和华南虎经过
- COCl2(g)CO(g)+Cl2(g) ΔH>0,当反应达到平衡时,下列措施:①升温 ②恒容通入惰性气体 ③增加CO浓
- 阅读下面的文字,完成1—3题。在不同文明间的交往交流中,语言从来就是变动不居的。从理论上说,语言交流应该是彼
- 茫茫黑夜中,航标灯为航海员指明了方向。航标灯的电源必须长效、稳定。我国科技工作者研制出以铝合金、Pt~Fe合金网为电极材
- --Where did you put my dictionary after using it this mornin
- 在Hg、Zn、Fe、Mg、Cu几种金属中: (1)在稀硫酸中反应最强烈的是 . (2)不能从盐酸中置换出氢的金属是 (3



