图形的旋转 知识点题库
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB交CD于点E.若AB=6,则△AEC的面积为( )

 C . 8
C . 8 D . 6
D . 6
如图,正△ABO的边长为2,O为坐标原点,A在  轴上,B在第二象限。△ABO沿
轴上,B在第二象限。△ABO沿  轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.
轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.

-
(1)
实验与探究

①在下列三个图中,给出菱形ABCD的顶点A,B,D的坐标(如图所示),写出图(1),(2),(3)中点C的坐标,它们分别是、、;
②菱形绕原点逆时针依照(90°,2)旋转后点C对应的点C1的坐标分别是、、.(其中(90°,2)表示旋转90°,长度扩大2倍)
-
(2) 归纳与发现
①在图4中,给出菱形ABCD的顶点A,B,D的坐标,求出顶点C的坐标;(点C的坐标用含a,b,c,d,e,f的代数式表示)
②菱形绕原点逆时针依照(90°,2)旋转后对应的C1的坐标为多少.
-
(3) 运用与推广
①通过对图(1),(2),(3),(4)的观察和顶点C的坐标的探究,你会发现:无论菱形ABCD处于直角坐标系的哪个位置,当顶点坐标为:A(a,b),B(c,d),C(m,n),D(e,f)时,四个顶点的横坐标a,c,m,e之间的等量关系为;纵坐标b,d,n,f之间的等量关系为(不必证明);
②通过顶点C的坐标和旋转后的C1的坐标探究,你会发现无论C点在哪个位置,绕原点逆时针依照(90°,n)旋转,设C(x1 , y1),C1(x2 , y2),则x1 , x2 , y1 , y2满足的等式是(不必证明).
(备注:有两点A(x1 , y1),B(x2 , y2),则它们的中点P的坐标为(
 ,
,  ))
))

小颖同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.
请你参考小颖同学的思路,探究并解决下列问题:

-
(1) 请你写出上面问题中线段PG与PC的位置关系;
-
(2) 将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题申的其他条件不变(如图2).你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明,

-
(1) 把△ABC绕点A旋转到图1,BD,CE的关系是(选填“相等”或“不相等”);简要说明理由;
-
(2) 若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图2中作出旋转后的图形,求PD的值,简要说明计算过程;
-
(3) 在(2)的条件下写出旋转过程中线段PD的最小值为,最大值为.



①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )

![]()
 B .
B .  C .
C .  D .
D . 
 后能与原来的图案里合,那么
后能与原来的图案里合,那么  的最小值是.
的最小值是. 

 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C . 

⑴将△ABC以点C为旋转中心旋转180°,得到△A1B1C , 请画出△A1B1C .
⑵平移△ABC , 使点A的对应点A2坐标为(﹣3,﹣4),请画出平移后对应的△A2B2C2 .
⑶若将△A1B1C绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.
 绕点
绕点 按顺时针方向旋转90°后得到
按顺时针方向旋转90°后得到 , 则下列四个图形中正确的是( )
, 则下列四个图形中正确的是( )
 B .
B .  C .
C .  D .
D . 

 的顶点均在格点上,点
的顶点均在格点上,点 ,
,  的坐标分别是
的坐标分别是 ,
,  , 把
, 把 绕点
绕点 逆时针旋转
逆时针旋转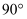 后得到
后得到 .
. 
⑴画出 , 直接写出点
, 直接写出点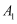 ,
,  的坐标;
的坐标;
⑵计算在旋转过程中, 所扫过的面积.
所扫过的面积.
⑶以原点 为位似中心,位似比为2,在第三象限画出
为位似中心,位似比为2,在第三象限画出 放大后的
放大后的 .
.
- 下图为初速度υ0沿直线运动的物体的速度图像
- (2013界安徽示范高中联考)动车把动力装置
- 下列对图的叙述中,不正确的是 (
- 有一个奇数列1,3,5,7,9,…,现在进行如
- Seeing their teacher __________ into the classroom, they sto
- 下列变化属于化学变化的是( )
- 对下面漫画所反映的历史观最有力的驳斥证据
- 以下说法中不正确的是( ) A. 质点的提出应
- 如图12-6-5所示,沿一条直线相向传播的两列波
- 如图所示,PD垂直于正方形ABCD所在平面,AB=2,E为P
- 如图所示为高等动物细胞及细胞膜的亚显微结
- 某一反应体系存在以下五种物质: Na2AsO3、H2O
- 中国在朝鲜战争与越南战争中相同的行动是(
- A
- 下表物质符合图中转化关系的是
- Can you __________ me 5 minutes ? I want your advice. A. g
- 阅读下面的文段,完成下面试题 �
- 请分别写出游标卡尺和螺旋测微器对应的读数
- 数列{an}中,a1=1,a2=6,an+2=an+1-an,求a2 005.
- 化简:=



