第一章计数原理知识点题库

如图所示，使电路接通，开关不同的开闭方法有（）

A . 11种 B . 20种 C . 21种 D . 12种

设 $\text{[math]}$ ，如果 $\text{[math]}$ =－6，则实数b的值为( )

A . $\text{[math]}$ B . － $\text{[math]}$ C . 2 D . －2

若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 81 B . 16 C . 8 D . 1

二项式 $\text{[math]}$ 的展开式中常数项是( )

A . 28 B . -7 C . 7 D . -28

$\text{[math]}$ 的展开式的常数项是（）

A . 1 B . 6 C . 15 D . 20

将 5 名学生分到 A,B,C 三个宿舍，每个宿舍至少 1 人至多 2 人，其中学生甲不到 A宿舍的不同分法有（）

A . 18 种 B . 36 种 C . 48 种 D . 60 种

1,4,5,x 四个不同数字组成四位数,所有这些四位数中的数字的总和为 288 ,则x=.

已知（2x+ $\text{[math]}$ ）⁴=a₀+a₁x+a₂x²+a₃x³+a₄x⁴ ，若a=（a₀+a₂+a₄）²﹣（a₁+a₃）² ，则 $\text{[math]}$ $\text{[math]}$ dx=

在x（1+x）⁶的展开式中，含x³项的系数为（）

A . 30 B . 20 C . 15 D . 10

某人解一道由两问组成的题，第一问用2种不同的方法，第二问用了3种不同的方法，解此题用了种不同的方法．

已知A_n^m=272，C_n^m=136，则m+n=．

安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（）

A . 12种 B . 18种 C . 24种 D . 36种

在（1+x）³+（1+x）⁴+…+（1+x）¹⁹的展开式中，含x²项的系数是．

已知（1﹣ $\text{[math]}$ ）•（1+x）⁵的展开式中x^r（r∈z且﹣1≤r≤5）的系数为0，则r=．

哈尔滨市冰雪节期间，5名游客到三个不同景点游览，每个景点至少有一人，至多两人，则不同的游览方法共有（）种.

A . 90 B . 60 C . 150 D . 125

直线 $\text{[math]}$ 与曲线 $\text{[math]}$ 在第一象限围成的封闭图形面积为 $\text{[math]}$ ，则 $\text{[math]}$ 展开式中， $\text{[math]}$ 的系数为（）

A . 20 B . -20 C . 5 D . -5

已知 $\text{[math]}$ 的展开式中 $\text{[math]}$ 的系数为108，则实数 $\text{[math]}$ .

已知数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，数列 $\text{[math]}$ 满足 $\text{[math]}$ ，

（1）求数列 $\text{[math]}$ 、 $\text{[math]}$ 的通项公式；
（2）求 $\text{[math]}$ .

第35届牡丹花会期间，我班有5名学生参加志愿者服务，服务场所是王城公园和牡丹公园.

（1）若学生甲和乙必须在同一个公园，且甲和丙不能在同一个公园，则共有多少种不同的分配方案？
（2）每名学生都被随机分配到其中的一个公园，设 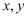$\text{[math]}$ 分别表示5名学生分配到王城公园和牡丹公园的人数，记 $\text{[math]}$ ，求随机变量 $\text{[math]}$ 的分布列和数学期望 $\text{[math]}$ .

用0，1，2，3，4，5这6个数字组成的没有重复数字的四位数中，能被5整除的数的个数为.（用数字作答）

<<
<
1
2
3
4
5
6
7
8
9
10
>
>>

最近更新

　