第一章 计数原理 知识点题库
设二项式 的展开式的各项系数的和为P,所有二项式系数的和为S,若有
的展开式的各项系数的和为P,所有二项式系数的和为S,若有 , 则n等于( )
, 则n等于( )
 的展开式的各项系数的和为P,所有二项式系数的和为S,若有
的展开式的各项系数的和为P,所有二项式系数的和为S,若有 , 则n等于( )
, 则n等于( )
A . 4
B . 5
C . 6
D . 8
将4个不同的球放入3个不同的盒中,每个盒内至少有1个球,则不同的放法种数为( )
A . 24
B . 36
C . 48
D . 96
(  )n的展开式的二项式系数之和为8,则展开式的常数项等于( )
)n的展开式的二项式系数之和为8,则展开式的常数项等于( )
 )n的展开式的二项式系数之和为8,则展开式的常数项等于( )
)n的展开式的二项式系数之和为8,则展开式的常数项等于( )
A . 4
B . 6
C . 8
D . 10
“五•一”期间某志愿者服务队准备从甲、乙等7名志愿者中选派4人参加A、B、C、D四个旅游景点的志愿服务,每个旅游景点安排1名志愿者,若要求甲、乙两志愿者至少有1人参加,那么这4名志愿者去四个旅游景点的安排方法共有( )种.
A . 30
B . 600
C . 720
D . 840
在(1﹣3x)6的展开式中,x2的系数为.(用数字作答)
在  的展开式中,常数项为.(用数字作答).
的展开式中,常数项为.(用数字作答).
 的展开式中,常数项为.(用数字作答).
的展开式中,常数项为.(用数字作答).
有5个男生和3个女生,从中选出5人担任5门不同学科的课代表,分别求符合下列条件的选法数:(结果用数字)
-
(1) 有女生但人数必须少于男生;
-
(2) 某女生一定要担任语文课代表;
-
(3) 某男生必须包括在内,但不担任数学课代表;
-
(4) 选取3名男生和2名女生分别担任5门不同学科的课代表,但数学课代表必须由男生担任,语文课代表必须由女生担任.
设  (n∈N*,an∈Z,bn∈Z).
(n∈N*,an∈Z,bn∈Z).
 (n∈N*,an∈Z,bn∈Z).
(n∈N*,an∈Z,bn∈Z).
-
(1) 求证:an2﹣8bn2能被7整除;
-
(2) 求证:bn不能被5整除.
在  的展开式中,记
的展开式中,记  项的系数为
项的系数为  ,则
,则  +
+  +
+  +
+  =( )
=( )
 的展开式中,记
的展开式中,记  项的系数为
项的系数为  ,则
,则  +
+  +
+  +
+  =( )
=( )
A . 45
B . 60
C . 120
D . 210
设  ,
,  ,在集合
,在集合  的所有元素个数为2的子集中,把每个子集的较大元素相加,和记为
的所有元素个数为2的子集中,把每个子集的较大元素相加,和记为  ,较小元素之和记为
,较小元素之和记为  .
.
 ,
,  ,在集合
,在集合  的所有元素个数为2的子集中,把每个子集的较大元素相加,和记为
的所有元素个数为2的子集中,把每个子集的较大元素相加,和记为  ,较小元素之和记为
,较小元素之和记为  .
.
-
(1) 当
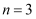 时,求
时,求  ,
,  的值;
的值;
-
(2) 求证:为任意的
 ,
,  ,
, 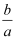 为定值.
为定值.
 的展开式中常数项为( )
的展开式中常数项为( )
A . -240
B . -160
C . 240
D . 160
某学校安排甲、乙、丙、丁四位同学参加数学、物理、化学竞赛,要求每位同学仅报一科,每科至少有一位同学参加,且甲、乙不能参加同一学科,则不同的安排方法有( )
A . 36种
B . 30种
C . 24种
D . 6种
现有5位学生站成一排照相,要求  和
和  两位学生均在学生
两位学生均在学生  的同侧,则不同的排法共有种(用数字作答).
的同侧,则不同的排法共有种(用数字作答).
 和
和  两位学生均在学生
两位学生均在学生  的同侧,则不同的排法共有种(用数字作答).
的同侧,则不同的排法共有种(用数字作答).
已知  展开式的二项式系数和为64,则其展开式中含
展开式的二项式系数和为64,则其展开式中含  项的系数是.
项的系数是.
 展开式的二项式系数和为64,则其展开式中含
展开式的二项式系数和为64,则其展开式中含  项的系数是.
项的系数是.
 的展开式中的常数项为160,则
的展开式中的常数项为160,则  的值为( )
的值为( )
A . -2
B . 2
C . -4
D . 4
如图,一只蚂蚁在  处觅食(蚂蚁只能走黑色实线),
处觅食(蚂蚁只能走黑色实线),  处有一块巧克力,蚂蚁找到巧克力的最短路径爬法有( )
处有一块巧克力,蚂蚁找到巧克力的最短路径爬法有( )
 处觅食(蚂蚁只能走黑色实线),
处觅食(蚂蚁只能走黑色实线),  处有一块巧克力,蚂蚁找到巧克力的最短路径爬法有( )
处有一块巧克力,蚂蚁找到巧克力的最短路径爬法有( )

A . 210种
B . 72种
C . 35种
D . 12种
已知王大爷养了5只鸡和3只兔子,晚上关在同一间房子里,清晨打开房门,这些鸡和兔子随机逐一向外走,则恰有2只兔子相邻走出房子的概率为( )
A .  B .
B . 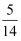 C .
C .  D .
D . 
 B .
B . 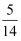 C .
C .  D .
D . 
若 , 则
, 则 .
.
 , 则
, 则 .
.
 的展开式中,
的展开式中, 的系数为
的系数为 , 则
, 则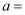 .
.
若二项式 的展开式中
的展开式中 的系数是84,则实数
的系数是84,则实数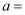 ( )
( )
 的展开式中
的展开式中 的系数是84,则实数
的系数是84,则实数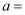 ( )
( )
A . 2
B .  C . 1
D .
C . 1
D . 
 C . 1
D .
C . 1
D . 
最近更新
- “长鞭呀,那个一呀摔呀,拍拍地响哎,……沿着社会主义大道奔前方……”这是过去的一首老歌的歌词,它反映了农民满怀豪情走上社
- 下列反应的离子方程式正确的是 A.用氯化铁溶液腐蚀铜板:Fe3++Cu=Fe2++Cu2+ B.将银片投入到
- 下列电池工作时,O2在正极放电的是( ) A.锌锰电池 B.氢燃料电池 C.铅蓄电池 D.镍镉电池
- 下列分类单位中,理论上讲生物种类最多的是 ( ) A、 科 B、 属 C
- 补写出下列名篇名句中的空缺部分。 (1)送子涉淇,至于顿丘。 , 。将子无怒,秋以为期
- (本小题满分12分)为迎接国庆60周年,美化城市,某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,如图所示。要
- 把500 mL含有BaCl2和KCl的混合溶液分成5等份,取一份加入含a mol硫酸钠的溶液,恰好使钡离子完全沉淀;另取
- 下列有关《茶花女》的说法,不正确的是() A.由意大利音乐家威尔第所创 B.表达了强烈的爱国主义思想和民族意识 C.威尔
- Mrs Black doesn’t believe her son is able to design a digita
- 向烧杯中逐滴加入x溶液至过量(图1),生成沉淀或气体的质量与加入x溶液的质量关系符合图2的是() 烧杯中的物质 x溶液
- 【2013年·黑龙江省牡丹江市】 【试题】4.仿写句子。(2分) 豁达是一种境界,一种品质。不要因为被别人误会而心怀怨恨
- 东汉时期,用树皮、麻头、破布和旧渔网等制成新书写材料的人是( )A.沈括 B.蔡伦 C
- A、B、C是同一周期的三种相邻的短周期元素,它们的最高价氧化物都能与NaOH(aq)反应,但只有一种能溶于水,C的一种最
- A、B、C、D四种短周期元素,原子序数依次增大,A原子的最外层上有4个电子;B的阴离子和C的阳离子具有相同的电子层结构,
- 如图所示烧杯中均盛有海水,铁在其中被腐蚀时由快到慢的顺序是( ) A.(4) (3) (2) (1)
- “鸟类的黑手党”﹣﹣杜鹃,将自己的卵产到别的小鸟巢中,小鸟辛勤地为杜鹃孵卵并精心喂食杜鹃的雏鸟.对小鸟这种行为的解释,
- 小明家购买了某品牌电冰箱,花去了1850元,这1850元是:①货币在执行流通手段职能 ②货币在执行价值尺度职能 ③观念形
- 世界上的火山、地震,大多发生在 ( )A.板块内部 B.大洋的沿岸 C.板块与
- 作文 人生中有很多扇门。推开那扇门,我们可以结交新朋友,可以认识新世界,可以悟出新道理请以“轻轻推开那扇门”为题,写一篇
- 如图所示,如果电阻R的数值和各电流表与电压表的示数都已知,哪一个图中的数据无法让我们计算出灯泡L的功率 ( )



