4.1 二项分布 知识点题库
某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为  和p.
和p.
 和p.
和p.
-
(1) 若在任意时刻至少有一个系统不发生故障的概率为
 ,求p的值;
,求p的值;
-
(2) 设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
某学校有两个食堂,甲、乙、丙三名学生各自随机选择其中的一个食堂用餐,则他们在同一个食堂用餐的概率为.
某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03,丙级品的概率为0.02,则抽查一件产品是正品的概率为.
甲、乙两人各进行一次射击,如果两人击中目标的概率是0.8.计算,至少有1人击中目标的概率.
甲乙两队进行排球比赛,已知在一局比赛中甲队获胜的概率是  ,没有平局.若采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于(用分数作答).
,没有平局.若采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于(用分数作答).
 ,没有平局.若采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于(用分数作答).
,没有平局.若采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于(用分数作答).
小明的妈妈为小明煮了5个粽子,其中两个腊肉馅三个豆沙馅,小明随机取出两个,事件A=“取到的两个为同一种馅”,事件B=“取到的两个都是豆沙馅”,则P(B|A)=( )
A .  B .
B .  C .
C . 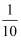 D .
D . 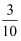
 B .
B .  C .
C . 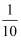 D .
D . 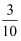
如图是一块高尔顿板示意图:在一块木板上钉着若干排互相平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,小球从上方的通道口落下后,将与层层小木块碰撞,最后掉入下方的某一个球槽内.若小球下落过程中向左、向右落下的机会均等,则小球最终落入③号球槽的概率为( )

A .  B .
B .  C .
C .  D .
D . 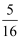
 B .
B .  C .
C .  D .
D . 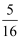
某射手每次射击击中目标的概率都是  ,则这名射手在3次射击中恰有2次击中目标的概率为( )
,则这名射手在3次射击中恰有2次击中目标的概率为( )
 ,则这名射手在3次射击中恰有2次击中目标的概率为( )
,则这名射手在3次射击中恰有2次击中目标的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某射手打靶命中8环、9环、10环的概率分别为0.15.0.25.0.2.如果他连续打靶三次,且每次打靶的命中结果互不影响.
-
(1) 求该射手命中29环的概率;
-
(2) 求该射手命中不少于28环的概率.
小夏经营一家夜市摊点,她准备参加当地为期5天的饮食文化节,期间每天获利与是否下雨有关:如果不下雨每天可获利1000元,如果下雨每天将亏损200元,气象资料显示饮食文化节期间每天下雨的概率是0.2,且每天下雨与否相互独立.
-
(1) 求饮食文化节开始后,直到第3天才下雨的概率;
-
(2) 在饮食文化节期间小夏获利的期望是多少?
四张外观相同的奖券让甲,乙,丙,丁四人各随机抽取一,其中只有一张奖券可以中奖,则( )
A . 四人中奖概率与抽取顺序无关
B . 在甲未中奖的条件下,乙或丙中奖的概率为  C . 事件甲或乙中奖与事件丙或丁中奖互斥
D . 事件甲中奖与事件乙中奖互相独立
C . 事件甲或乙中奖与事件丙或丁中奖互斥
D . 事件甲中奖与事件乙中奖互相独立
 C . 事件甲或乙中奖与事件丙或丁中奖互斥
D . 事件甲中奖与事件乙中奖互相独立
C . 事件甲或乙中奖与事件丙或丁中奖互斥
D . 事件甲中奖与事件乙中奖互相独立
有  个相同的球,分别标有数字
个相同的球,分别标有数字  ,从中有放回的随机取两次,每次取1个球.用
,从中有放回的随机取两次,每次取1个球.用  表示试验的样本点,其中
表示试验的样本点,其中  表示第一次取出的基本结果,
表示第一次取出的基本结果,  表示第二次取出的基本结果.
表示第二次取出的基本结果.
 个相同的球,分别标有数字
个相同的球,分别标有数字  ,从中有放回的随机取两次,每次取1个球.用
,从中有放回的随机取两次,每次取1个球.用  表示试验的样本点,其中
表示试验的样本点,其中  表示第一次取出的基本结果,
表示第一次取出的基本结果,  表示第二次取出的基本结果.
表示第二次取出的基本结果.
-
(1) 写出这个试验的样本空间
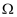 ;
;
-
(2) 用
 表示事件“第一次取出的球的数字是1”;用
表示事件“第一次取出的球的数字是1”;用  表示事件“两次取出的球的数字之和是4”,求证:
表示事件“两次取出的球的数字之和是4”,求证:  .
.
设随机变量  服从二项分布
服从二项分布  ,则
,则  等于( )
等于( )
 服从二项分布
服从二项分布  ,则
,则  等于( )
等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
为巩固拓展脱贫攻坚成果,某地区对地方特色手工艺品的质量实行专家鉴定制度:若一件手工艺品被3位专家都鉴定通过,则该手工艺品被评为一级品;若一件手工艺品仅有两位专家鉴定通过,则该手工艺品被评为二级品;若一件手工艺品仅有一位专家鉴定通过,则该手工艺品被评为三级品;若一件手工艺品没有得到三位专家的鉴定通过,则相应的被评为四级品.已知每一件手工艺品被一位专家鉴定通过的概率为  ,且专家之间鉴定是否通过相互独立.
,且专家之间鉴定是否通过相互独立.
 ,且专家之间鉴定是否通过相互独立.
,且专家之间鉴定是否通过相互独立.
-
(1) 求一件手工艺品被专家鉴定为二级品的概率;
-
(2) 若一件手工艺品质量分别为一、二、三级均可出厂,且利润分别为100元,70元,20元,质量为四级品不能出厂,亏损10元,记一件手工艺品的利润为
 元,求
元,求  的分布列与及1000件产品的平均利润.
的分布列与及1000件产品的平均利润.
高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图所示的小木块中,上面7层为高尔顿板,最下面一层为改造的高尔顿板,小球从通道口落下,第一次与第2层中间的小木块碰撞,以  的概率向左或向右滚下,依次经过7次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前6次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以
的概率向左或向右滚下,依次经过7次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前6次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以  的概率向左滚下,或在前6次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以
的概率向左滚下,或在前6次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以  的概率向右滚下.
的概率向右滚下.
 的概率向左或向右滚下,依次经过7次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前6次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以
的概率向左或向右滚下,依次经过7次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前6次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以  的概率向左滚下,或在前6次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以
的概率向左滚下,或在前6次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以  的概率向右滚下.
的概率向右滚下. 
-
(1) 若进行一次高尔顿板试验,求小球落入第7层第6个空隙处的概率;
-
(2) 小明同学在研究了高尔顿板后,利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动,8元可以玩一次高尔顿板游戏,小球掉入X号球槽得到的奖金为ξ元.其中ξ=|20﹣5X|.
①求X的分布列:
②高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小明同学能盈利吗?
“坚持五育并举,全面发展素质教育,强化体育锻炼”这是我们现阶段教育必须坚持的.甲乙两人为了培养自己的体育素养,分别进行乒乓球和羽毛球两场比赛,两场比赛中,胜者得2分、败者得0分,每场比赛一定会分出胜负,其中甲在两场比赛中胜出的概率分别为:  和
和  ,每场比赛相互独立,谁最终得分多谁获胜.
,每场比赛相互独立,谁最终得分多谁获胜.
 和
和  ,每场比赛相互独立,谁最终得分多谁获胜.
,每场比赛相互独立,谁最终得分多谁获胜.
-
(1) 求甲获胜的概率;
-
(2) 求甲得分的分布列及数学期望.
某校篮球社组织一场篮球赛,参赛队伍为甲、乙两队,比赛实行三局两胜制,已知甲队赢得每一局比赛的概率为p( ).
).
 ).
).
-
(1) 若最终甲队获胜的概率为
 , 求乙队赢得每一局比赛的概率.
, 求乙队赢得每一局比赛的概率.
-
(2) 在(1)成立的情况下,在每一局比赛中,赢的队伍得2分,输的队伍得1分.用X表示比赛结束时两支球队的得分总和,求随机变量x的分布列和期望.
甲乙两名射击运动员进行射击比赛,甲射击击中靶子的概率为0.6,乙射击击中靶子概率为0.8,则"恰好有一人击中靶子"的概率为;"至少有一个人击中靶子”"的概率为.
某企业对生产设备进行优化升级,升级后的设备控制系统由 个相同的元件组成,每个元件正常工作的概率均为
个相同的元件组成,每个元件正常工作的概率均为 , 各元件之间相互独立.当控制系统有不少于
, 各元件之间相互独立.当控制系统有不少于 个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为 (例如:
(例如: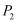 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).
 个相同的元件组成,每个元件正常工作的概率均为
个相同的元件组成,每个元件正常工作的概率均为 , 各元件之间相互独立.当控制系统有不少于
, 各元件之间相互独立.当控制系统有不少于 个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为 (例如:
(例如: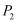 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).
-
(1) 若
 , 当
, 当 时,求控制系统中正常工作的元件个数
时,求控制系统中正常工作的元件个数 的分布列和数学期望,并求
的分布列和数学期望,并求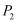 ;
;
-
(2) 升级后的设备控制系统原有
 个元件,现再增加2个相同的元件,用
个元件,现再增加2个相同的元件,用 ,
,  ,
,  表示新升级的设备正常运行的概率
表示新升级的设备正常运行的概率 . (注:不用求
. (注:不用求 )
)
设随机变量 , 则
, 则 等于.
等于.
 , 则
, 则 等于.
等于.
最近更新
- 长征是中国工农红军进行的伟大战略转移。这里的“转移”是指 ( ) A.党的工作重心的转移
- Jo was doing a lot of exercise to build up her . A. str
- (4分)在用如下图所示的装置做“探究功与速度变化的关系”的实验时,下列说法正确的是().A.为了平衡摩擦力,实验中可以将
- 现行元素周期表中已列出112种元素,其中元素种类最多的周期是( )A.第四周期 B.第五周期 C
- 在10分钟的时间内,分针转过的角度是( )A.15°B.30°C.15°D.60°
- 基因型为AAbbCC与aaBBcc的小麦进行杂交,这三对等位基因分别位于非同源染色体上,F1杂种形成的配子种类数和F2的
- 在“组成串联电路”的学生实验中,如图所示是小林同学实验的电路图,当开关S合上后,他发现灯L1与L2均不亮。小林同学想了想
- 设,则( ) A. 与都是奇函数 B. 是奇函数,是偶函数 C. 与都是偶函数 D. 是偶函数
- 2016年2月24日,全国质检系统法制工作会议指出,坚持依法治国,是“十三五”时期必须遵循的原则之一,要用更高的站位提
- 下图中,正方形代表亚欧大陆,黑色阴影表示中国.图中阴影能正确反映中国位置的是( )
- 某短周期非金属元素R的原子核外最外层电子数是次外层电子数的一半,有关该元素的下列说法正确的是 A. 在自然界中只以化合态
- 如图甲为理想变压器,其原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,原线圈接如图乙所示的正弦交流电,图中R1为
- 物体做匀变速直线运动,某时刻速度的大小为2m/s,2s后速度的大小变为6m/s,则在这2s内,关于该物体的运动情况说法正
- 作文 带上欣赏的眼睛,你会由衷地赞叹“生活真好”;打开心灵的窗户,你会由衷地赞叹“有亲情真好”;怀着博大的胸怀,你会由衷
- 有关工业地域的叙述,正确的是 ①工业联系导致工业集聚,形成工业地域②自发形成
- 下列有关ATP的叙述,其中正确的是( ) A.一个ATP分子水解可以生成一个脱氧核苷酸分子和两个磷酸分子 B.植物
- 复数(为虚数单位)的实部等于_________.
- 一个负数减去它的相反数后,再除以这个负数的绝对值,所得商为__________.
- 从《上海县竹枝词》中,可以知道许多古代的节日习俗,其中与端午节相关的是( ) A.拜年未了接财神,爆竹通宵闹比
- 隋朝的统治类似于 ()A、秦朝 B、东汉 C、西晋 D、东晋



