4.1 二项分布 知识点题库

①第二次击中目标的概率是0.8;
②恰好击中目标三次的概率是0.83×0.2;
③至少击中目标一次的概率是1﹣0.24;
其中正确的结论的序号是 (写出所有正确结论的序号)
(A)在第5次测试后停止;
(B)在第10次测试后停止.
 以小数点前的一位数字为茎,小数点后的一位数字为叶
以小数点前的一位数字为茎,小数点后的一位数字为叶  :
: 
-
(1) 指出这组数据的众数和中位数;
-
(2) 若满意度不低于
 分,则称该被调查者的满意度为“极满意”
分,则称该被调查者的满意度为“极满意”  求从这16人中随机选取3人,至少有2人是“极满意”的概率;
求从这16人中随机选取3人,至少有2人是“极满意”的概率;
-
(3) 以这16人的样本数据来估计整个被调查群体的总体数据,若从该被调查群体
 人数很多
人数很多  任选3人,记
任选3人,记  表示抽到“极满意”的人数,求
表示抽到“极满意”的人数,求  的分布列及数学期望.
的分布列及数学期望.
 、
、  、
、  ,且每题答对与否相互独立.
,且每题答对与否相互独立.
-
(1) 当
 时,求考生填空题得满分的概率;
时,求考生填空题得满分的概率;
-
(2) 若考生填空题得10分与得15分的概率相等,求
 的值.
的值.
-
(1) 某人抽奖一次,求其获奖金额X的概率分布和数学期望;
-
(2) 赵四购物恰好满600元,假设他不放弃每次抽奖机会,求他获得的奖金恰好为60元的概率.
 大致服从正态分布
大致服从正态分布  ,且规定尺寸
,且规定尺寸  为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下: 
-
(1) 估计生产线生产的零件的次品率及零件的平均尺寸;
-
(2) 从生产线上随机取一箱零件,求这箱零件销售后的期望利润及不亏损的概率.
|
每分钟跳绳个数 |
| | | | 185以上 |
| 得分 | 16 | 17 | 18 | 19 | 20 |
年级组为了了解学生的体质,随机抽取了100名学生,统计了他的跳绳个数,并绘制了如下样本频率直方图:

-
(1) 现从这100名学生中,任意抽取2人,求两人得分之和小于35分的概率(结果用最简分数表示);
-
(2) 若该校高二年级2000名学生,所有学生的一分钟跳绳个数
 近似服从正态分布
近似服从正态分布  ,其中
,其中  ,
, 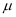 为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题: ①估计每分钟跳绳164个以上的人数(四舍五入到整数)
②若在全年级所有学生中随机抽取3人,记每分钟跳绳在179个以上的人数为
 ,求
,求  的分布列和数学期望与方差.
的分布列和数学期望与方差.(若随机变量
 服从正态分布
服从正态分布  则
则  ,
,  ,
,  )
)
 “抽取的两个小球标号之和大于5”,事件
“抽取的两个小球标号之和大于5”,事件  “抽取的两个小球标号之积大于8”,则( )
“抽取的两个小球标号之积大于8”,则( )
 B . 事件
B . 事件  发生的概率为
发生的概率为 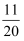 C . 事件
C . 事件  发生的概率为
发生的概率为  D . 从甲罐中抽到标号为2的小球的概率为
D . 从甲罐中抽到标号为2的小球的概率为 
|
潜伏期 (单位:天) |
| | | | | | |
| 人数 | 85 | 205 | 310 | 250 | 130 | 15 | 5 |
-
(1) 该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表.请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关;
潜伏期≤6天
潜伏期>6天
总计
50岁以上(含50岁)
100
50岁以下
55
总计
200
-
(2) 以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该研究团队随机调查了20名患者,设潜伏期超过6天的人数为
 ,则
,则  的期望是多少?
的期望是多少? 附:

0.05
0.025
0.010

3.841
5.024
6.635
 其中
其中  .
.
 ,其必答环节的总得分为
,其必答环节的总得分为  ,则( )
,则( )
 B .
B .  C .
C .  D .
D . 
 , 统计得到以下
, 统计得到以下 列联表,经过计算可得
列联表,经过计算可得 .
.男生 | 女生 | 合计 | |
了解 |
| ||
不了解 |
| ||
合计 |
|
|
附: .
.
-
(1) 求
 的值,并判断有多大的把握认为该校学生对冬季奥运会项目的了解情况与性别有关;
的值,并判断有多大的把握认为该校学生对冬季奥运会项目的了解情况与性别有关;
-
(2) ①为弄清学生不了解冬季奥运会项目的原因,采用分层抽样的方法从抽取的不理解冬季奥运会项目的学生中随机抽取9人,再从这9人中抽取
 人进行面对面交流,“至少抽到一名女生”的概率;
人进行面对面交流,“至少抽到一名女生”的概率;②将频率视为概率,用样本估计总体,从该校全体学生中随机抽取10人,记其中对冬季奥运会项目了解的人数为
 , 求
, 求 的数学期望.
的数学期望.附表:

0.10
0.05
0.025
0.010
0.001

2.706
3.841
5.024
6.635
10.828
月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | 合计 |
空气质量优良天数 | 24 | 18 | 11 | 27 | 23 | 21 | 26 | 29 | 27 | 29 | 23 | 30 | 288 |
空气质量污染天数 | 7 | 10 | 20 | 3 | 8 | 9 | 5 | 2 | 3 | 2 | 7 | 1 | 77 |
-
(1) 从2021年中任选1天,求这一天空气质量优良的概率;
-
(2) 从2021年的4月、6月和9月中各任选一天,设随机变量X表示选出的3天中质量优良的天数,求X的分布列;
-
(3) 在2021年的1月、3月、5月、7月、8月、10月、12月中,设空气质量优良天数的方差为
 , 空气质量污染天数的方差为
, 空气质量污染天数的方差为 , 试判断
, 试判断 ,
,  的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
日销量(枝) | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 20 | 20 | 10 | 15 | 12 | 11 | 12 |
-
(1) 若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天销量n(单位:枝,
 )的函数解析式;
)的函数解析式;
-
(2) 根据所列表格数据,以100天记录的日销量的频率作为概率
①若花店两天的销量互不影响,求两天一共售出30枝玫瑰花的概率;
②若花店计划一天购进16枝或17枝玫瑰花,以两种情况的利润的期望值作为依据,你认为应购进16枝还是17枝?
 , 记
, 记 ,
,  , 1,2,…,n.在研究
, 1,2,…,n.在研究 的最大值时,该小组同学发现:若
的最大值时,该小组同学发现:若 为正整数,则
为正整数,则 时,
时, , 此时这两项概率均为最大值;若
, 此时这两项概率均为最大值;若 为非整数,当k取
为非整数,当k取 的整数部分,则
的整数部分,则 是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的骰子并实时记录点数1出现的次数,当投掷到第35次时,记录到此时点数1出现5次,若继续再进行65次投掷试验,则当投掷到第100次时,点数1一共出现的次数为的概率最大.
是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的骰子并实时记录点数1出现的次数,当投掷到第35次时,记录到此时点数1出现5次,若继续再进行65次投掷试验,则当投掷到第100次时,点数1一共出现的次数为的概率最大.
 , 且每一局的胜者,在接下来一局获胜的概率为
, 且每一局的胜者,在接下来一局获胜的概率为 .
.
-
(1) 求两人打完三局恰好结束比赛的概率;
-
(2) 设比赛结束时总的比赛局数为随机变量X,求X的数学期望
 .
.
 ,
,  .
.
-
(1) 若
 , 求
, 求 ,
,  ;
;
-
(2) 若
 ,
,  互斥,求
互斥,求 ,
,  ;
;
-
(3) 若
 ,
,  相互独立,求
相互独立,求 ,
,  .
.
 ,
,  ,则p=.
,则p=.
 . 已知该同学一周有3天骑车上学.
. 已知该同学一周有3天骑车上学.
-
(1) 求该同学在这3天上学途中恰有1天遇到红灯的概率;
-
(2) 记该同学在这3天上学途中遇到红灯的天数为
 , 求
, 求 的分布列及数学期望
的分布列及数学期望 .
.
- 一个从地面竖直上抛的物体,它两次经过同一较低a点的时间间隔为Ta,两次经过另一较高的b点的时间间隔为Tb,则ab两点间的
- 在“碰撞中的动量守恒”实验中,已测得A、B两小球质量mA<mB,由实验所得结果如图8—7—7所示,图中M、P、N为
- 下图中,若甲代表水和二氧化碳,则( )A.Ⅱ是呼吸作用,乙是有机物和氧气,Ⅰ是光合作用 B.Ⅱ是光合作用,乙是二氧化
- 18.下列各句,没有语病、句意明确的一句是( )(3分)A.这次招聘,一半以上的应聘者曾多年担任外资企业的中高层管
- 右图为下丘脑中某细胞的部分膜结构示意图,下列叙述正确的是( ) A.若此图为突触后膜局部结构,则兴奋经过此处时的信
- 如图所示,靠在竖直粗糙墙壁上的物块在t=0时被无初速释放,此时开始受到一随时间变化规律为的水平力作用.、、和分别表示物块
- British writer JohnBunyan was born at Elstow, Bedfordshire,
- 棱长为2 cm的正方体容器盛满水,把半径为1 cm的铜球放入水中刚好被淹没.然后再放入一个铁球,使它淹没水中,要使流出来
- 现代医学表明:人类牙齿是由一层叫碱式磷酸钙的坚硬物质保护着.这种碱式磷酸钙的化学式可表示为[Ca5(OH)(PO4)3]
- 我国婚姻法明确规定:“直系血亲和三代之内的旁系血亲禁止结婚”,对任何一个人来说,在下列血亲关系中属于旁系血亲的是() ①
- (一) 某科学家设计了一个光合作用的实验。实验前,他向一个密闭容器的溶液中加进了一定量的ATP、NADPH、磷酸盐、光合
- 在1932年的美国总统选举中,民主党候选人罗斯福当选总统。面对“大萧条”,他坚定地认为,这需要国家进行大胆的、坚持不懈的
- 如图,平面直角坐标系中,已知直线上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转900至线段PD,
- X、R是两种金属,能发生反应:X+3RNO3===3R+X(NO3)3下列说法不正确的是 A.该反应是置换反应
- 木块在水平恒力F作用下,由静止开始在水平路面上前进s,随即撤去此恒力后又前进2s才停下来。设运动全过程中路面情况相同,则
- 已知x, y满足约束条件的最大值为( ) A.3 B.-3 C.1 D.
- 质量m=100 kg的小船静止在静水中,船两端载着m甲=40 kg,m乙=60 kg的游泳者,在同一水平线上甲朝左乙朝右
- 基因工程等生物高科技的广泛应用,引发了“关于科技和伦理”的争论。有人欢呼,科学技术的发展将改变一切;有人惊呼,它将引发道
- 20世纪90年代,有人把中国东部经济发展状态比作“满弓待发之箭”:“弓”比喻为1984年国家开放的十四个沿海港口城市;“
- 中央电视台开播《百家讲坛》以后,一些艰涩高深的传统经典经过现代诠释变得通俗易懂,富有时代气息,为大众所接受。这说明 A.

















