4.1 二项分布 知识点题库
在图所示的电路中,5只箱子表示保险匣,箱中所示数值表示通电时保险丝被切断的概率,当开关合上时,电路畅通的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
甲乙两人下棋,若甲获胜的概率为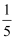 , 甲乙下成和棋的概率为
, 甲乙下成和棋的概率为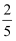 , 则乙不输棋的概率为 .
, 则乙不输棋的概率为 .
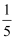 , 甲乙下成和棋的概率为
, 甲乙下成和棋的概率为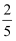 , 则乙不输棋的概率为 .
, 则乙不输棋的概率为 .
长沙天心区某中学举行春季运动会,高三某班李萍同学参加女子乒乓球单打比赛.假定从开始的小组淘汰赛到最后决定出冠亚军共经过5轮比赛.若李萍同学在5轮比赛中顺利过关的概率依次为 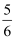 ,
,  ,
,  ,
,  ,
,  试问:
试问:
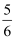 ,
,  ,
,  ,
,  ,
,  试问:
试问:(Ⅰ)李萍同学获得该项冠军的可能性有多大?
(Ⅱ)李萍同学在第二轮或第三轮被淘汰的概率是多少?
一批产品次品率为4%,正品中一等品率为75%.现从这批产品中任取一件,恰好取到一等品的概率为( )
A . 0.75
B . 0.71
C . 0.72
D . 0.3
一名工人维护3台独立的游戏机,一天内3台需要维护的概率分别为0.9、0.8和0.85,则一天内至少有一台游戏机不需要维护的概率为(结果用小数表示)
将一枚硬币连续投掷3次,则恰有连续2次出现正面朝上的概率是.
在如图所示的电路图中,开关  闭合与断开的概率都是
闭合与断开的概率都是  ,且是相互独立的,则灯灭的概率是( )
,且是相互独立的,则灯灭的概率是( )
 闭合与断开的概率都是
闭合与断开的概率都是  ,且是相互独立的,则灯灭的概率是( )
,且是相互独立的,则灯灭的概率是( ) 
A . 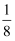 B .
B . 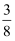 C .
C . 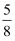 D .
D . 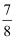
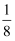 B .
B . 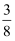 C .
C . 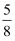 D .
D . 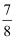
某工厂的检验员为了检测生产线上生产零件的情况,从产品中随机抽取了  个进行测量,根据所测量的数据画出频率分布直方图如下:
个进行测量,根据所测量的数据画出频率分布直方图如下:
 个进行测量,根据所测量的数据画出频率分布直方图如下:
个进行测量,根据所测量的数据画出频率分布直方图如下: 
如果:尺寸数据在  内的零件为合格品,频率作为概率.
内的零件为合格品,频率作为概率.
-
(1) 从产品中随机抽取
 件,合格品的个数为
件,合格品的个数为  ,求
,求  的分布列与期望:
的分布列与期望:
-
(2) 为了提高产品合格率,现提出
 ,
,  两种不同的改进方案进行试验,若按
两种不同的改进方案进行试验,若按  方案进行试验后,随机抽取
方案进行试验后,随机抽取  件产品,不合格个数的期望是
件产品,不合格个数的期望是  :若按
:若按  方案试验后,抽取
方案试验后,抽取  件产品,不合格个数的期望是
件产品,不合格个数的期望是  ,你会选择哪个改进方案?
,你会选择哪个改进方案?
为迎接“五一”节的到来,某单位举行“庆五一,展风采”的活动.现有6人参加其中的一个节目,该节目由  两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数n和m,并在屏幕的下方计算出
两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数n和m,并在屏幕的下方计算出  的值.现规定:每个人去按“Enter”键,当显示出来的
的值.现规定:每个人去按“Enter”键,当显示出来的  小于
小于  时则参加
时则参加  环节,否则参加B环节.
环节,否则参加B环节.
 两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数n和m,并在屏幕的下方计算出
两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数n和m,并在屏幕的下方计算出  的值.现规定:每个人去按“Enter”键,当显示出来的
的值.现规定:每个人去按“Enter”键,当显示出来的  小于
小于  时则参加
时则参加  环节,否则参加B环节.
环节,否则参加B环节.
-
(1) 求这6人中恰有2人参加该节目A环节的概率;
-
(2) 用
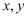 分别表示这6个人中去参加该节目
分别表示这6个人中去参加该节目  两个环节的人数,记
两个环节的人数,记  ,求随机变量
,求随机变量  的分布列与数学期望.
的分布列与数学期望.
如图,  表示三个开关,设在某段时间内它们正常工作的概率分别是0.9、0.8、0.7,那么该系统正常工作的概率是( ).
表示三个开关,设在某段时间内它们正常工作的概率分别是0.9、0.8、0.7,那么该系统正常工作的概率是( ).
 表示三个开关,设在某段时间内它们正常工作的概率分别是0.9、0.8、0.7,那么该系统正常工作的概率是( ).
表示三个开关,设在某段时间内它们正常工作的概率分别是0.9、0.8、0.7,那么该系统正常工作的概率是( ). 
A . 0.994
B . 0.686
C . 0.504
D . 0.496
甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,
答错得零分.假设甲队中每人答对的概率均为  ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为  且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
(Ⅰ)求随机变量  分布列;
分布列;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:  ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
 ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图: 
-
(1) 若该样本中男生有55人,试估计该学校高三年级女生总人数;
-
(2) 若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
-
(3) 若规定分数在
 为“良好”,
为“良好”,  为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
棋盘上标有第0,1,2,…,100站,棋子开始时位于第0站,棋手抛掷均匀硬币走跳棋游戏.若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第99站或第100站时,游戏结束.设棋子跳到第n站的概率为Pn .
-
(1) 当游戏开始时若抛掷均匀硬币3次后求棋手所走站数之和X的分布列与数学期望;
-
(2) 证明:
 ;
;
-
(3) 求P99 , P100的值.
已知  ,并且
,并且  ,则方差
,则方差  ( )
( )
 ,并且
,并且  ,则方差
,则方差  ( )
( )
A .  B .
B . 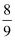 C .
C .  D .
D . 
 B .
B . 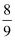 C .
C .  D .
D . 
已知事件  ,
,  ,且
,且  ,
,  ,则下列结论正确的是( )
,则下列结论正确的是( )
 ,
,  ,且
,且  ,
,  ,则下列结论正确的是( )
,则下列结论正确的是( )
A . 如果  ,那么
,那么  ,
,  B . 如果
B . 如果  与
与  互斥,那么
互斥,那么  ,
,  C . 如果
C . 如果  与
与  相互独立,那么
相互独立,那么  ,
,  D . 如果
D . 如果  与
与  相互独立,那么
相互独立,那么  ,
, 
 ,那么
,那么  ,
,  B . 如果
B . 如果  与
与  互斥,那么
互斥,那么  ,
,  C . 如果
C . 如果  与
与  相互独立,那么
相互独立,那么  ,
,  D . 如果
D . 如果  与
与  相互独立,那么
相互独立,那么  ,
, 
2020年5月27日,中央文明办明确规定,在2020年全国文明城市测评指标中不将马路市场、流动商贩列为文明城市测评考核内容.6月1日上午,国务院总理李克强在山东烟台考察时表示,地摊经济、小店经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机.其中套圈游戏凭借其趣味性和挑战性深受广大市民的欢迎,现有甲、乙两人进行套圈比赛,要求他们站在定点A , B两点处进行套圈,已知甲在A , B两点的命中率均为  ,乙在A点的命中率为
,乙在A点的命中率为  ,在B点的命中率为
,在B点的命中率为  ,且他们每次套圈互不影响.
,且他们每次套圈互不影响.
 ,乙在A点的命中率为
,乙在A点的命中率为  ,在B点的命中率为
,在B点的命中率为  ,且他们每次套圈互不影响.
,且他们每次套圈互不影响.
-
(1) 若甲在A处套圈4次,求甲至少命中2次的概率;
-
(2) 若甲和乙每人在A , B两点各套圈一次,且在A点命中计2分,在B点命中计3分,未命中则计0分,设甲的得分为
 ,乙的得分为
,乙的得分为  ,写出
,写出  和
和  的分布列和期望;
的分布列和期望;
-
(3) 在(2)的条件下,若
 ,求
,求  的取值范围
的取值范围
掷一枚硬币两次,记事件  “第一次出现正面”,
“第一次出现正面”,  “第二次出现反面”,下列结论正确的为( )
“第二次出现反面”,下列结论正确的为( )
 “第一次出现正面”,
“第一次出现正面”,  “第二次出现反面”,下列结论正确的为( )
“第二次出现反面”,下列结论正确的为( )
A .  B .
B .  C .
C .  与
与  互斥
D .
互斥
D .  与
与  相互独立
相互独立
 B .
B .  C .
C .  与
与  互斥
D .
互斥
D .  与
与  相互独立
相互独立
有一大批产品,其验收方案是:先从这批产品中取6件作检验,这6件产品中优质品的件数记为  (
(  ,
,  ),如果
),如果  则接收这产品,如果
则接收这产品,如果  则拒收;其他情况下做第二次检验,其做法是从产品中再另任取2件,逐一检验,若检验过程中检验出非优质品就要终止检验且拒收这批产品,否则继续产品检验,且仅当这2件产品都为优质品时接收这批产品.假设这批产品的优质品率为
则拒收;其他情况下做第二次检验,其做法是从产品中再另任取2件,逐一检验,若检验过程中检验出非优质品就要终止检验且拒收这批产品,否则继续产品检验,且仅当这2件产品都为优质品时接收这批产品.假设这批产品的优质品率为  ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
 (
(  ,
,  ),如果
),如果  则接收这产品,如果
则接收这产品,如果  则拒收;其他情况下做第二次检验,其做法是从产品中再另任取2件,逐一检验,若检验过程中检验出非优质品就要终止检验且拒收这批产品,否则继续产品检验,且仅当这2件产品都为优质品时接收这批产品.假设这批产品的优质品率为
则拒收;其他情况下做第二次检验,其做法是从产品中再另任取2件,逐一检验,若检验过程中检验出非优质品就要终止检验且拒收这批产品,否则继续产品检验,且仅当这2件产品都为优质品时接收这批产品.假设这批产品的优质品率为  ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
-
(1) 求这批产品被接收的概率;
-
(2) 若第一次检验费用固定为1000元,第二次检验费用为每件产品100元,记
 (单位:元)为整个产品检验过程中的总费用,求
(单位:元)为整个产品检验过程中的总费用,求  的分布列及数学期望.
的分布列及数学期望.
在一次活动课上,老师准备了4个大小完全相同的红包,其中只有一个红包里面有100元,其余三个里面都是白纸.老师邀请甲上台随机抽取一个红包,但不打开红包,然后老师从剩下的三个红包中拿走一个装有白纸的红包,甲此时可以选择将自己选中的红包与剩下的两个红包中的一个进行置换.
-
(1) 若以获得有100元的红包概率的大小作为评判的依据,甲是否需要选择置换?请说明理由.
-
(2) 以(1)中的结果作为置换的依据,记
 表示甲获得的金额,求
表示甲获得的金额,求 的分布列与期望.
的分布列与期望.
在—次实验中,同时抛掷4枚均匀的硬币16次,设4枚硬币正好出现3 枚正面向上,1 枚反面向上的次数为 , 则
, 则 的方差是( )
的方差是( )
 , 则
, 则 的方差是( )
的方差是( )
A . 3
B . 4
C . 1
D . 

最近更新
- Researches have shown that the first impression you make on
- 小王同学阅读了下表后,得出了一些结论,其中正确的是( )A. 不同的物质,密度一定不同 B.固体的密度都
- 下列叙述正确的是() A.电镀时,通常把待镀的金属制品作阳极 B.氯碱工业是电解熔融的NaCl,在阳极能得到Cl2 C.
- 已知:Ksp(AgCl)=1.8×10﹣10,Ksp(AgI)=1.5×10﹣16,Ksp(Ag2CrO4)=2.0×1
- —Where did you get your laptop? I’d like to get one. —Wel
- .如果在数轴上﹣1<a<0,b>1,那么下列判断正确的是() A.a+b<0 B.ab>0 C. D.a﹣
- 下表列出了除去物质中所含少量杂质的方法,其中错误的是 ( ) 物质 所含杂质 除去杂质的方法 A CuSO
- 有一则“守株待兔”的古代寓言,设兔子的头部受到大小等于自身重量的打击力时,即可致死。假设兔子与树桩作用时间大约为0.2秒
- 如图,是一块四边形钢板缺了一个角,根据图中所标出的测量结果,得所缺损的 ∠A的度数为_________.
- Music Club We have a good music teacher, Miss Lin, in
- 下列各组词语中,只有一个错别字的一组是( ) A.起迄 迄今为止 嘻嘻哈哈 业精于勤荒于嘻 B.旺季
- 如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的 三角形叫格点三角形,该图中与△ABC全等的不同格
- 下列各句中,没有病句的一句是(2分) A.关于《红楼梦》后40回的作者是谁这个问题,红学家历来有不同的说法,现在大家一般
- 实验室常用下列装置来制取氧气:(1)写出图中有标号仪器的名称:a 、b ; (2)用双氧水和二
- 请从下列物质中选择适当的物质填空:(4分)A.硝酸铵 C.氢气 D.天然气 E.生石灰
- 下列叙述中正确的是 ( ) A.人类利用的能量都是通过化学反应获得的 B.有放热现象发生的变化都是化学变化 C.
- 28.山西能源基地已建成我国最大火电基地,其电力主要输往 A.西南、西北地区 B.京津、华北地区 C
- 下图1是某种二倍体动物的细胞分裂示意图(局部),三个细胞均来自于同一个动物个体;下图2是该动物某种细胞分裂全过程中染色
- 已知命题,且,命题,且. (1)若,,求实数a的值; (2)若是的充分条件,求实数的取值范围.
- 已知O为△ABC的内心,且∠BOC=130°,则∠A=.



