4.1 二项分布 知识点题库
已知离散型随机变量X服从二项分布X~B(n,p)且E(X)=12,D(X)=4,则n与P 的值分别为 ( )
A . 18, B . 18,
B . 18, C . 12,
C . 12, D . 12,
D . 12,
 B . 18,
B . 18, C . 12,
C . 12, D . 12,
D . 12,
在某一试验中事件A出现的概率为 , 则在
, 则在 次试验中
次试验中 出现
出现 次的概率为( )
次的概率为( )
 , 则在
, 则在 次试验中
次试验中 出现
出现 次的概率为( )
次的概率为( )
A . 1- B .
B .  C . 1-
C . 1- D .
D . 
 B .
B .  C . 1-
C . 1- D .
D . 
已知 , 且
, 且 ,
,  , 则P等于( )
, 则P等于( )
 , 且
, 且 ,
,  , 则P等于( )
, 则P等于( )
A . 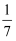 B .
B .  C .
C . 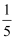 D .
D . 
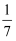 B .
B .  C .
C . 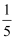 D .
D . 
甲乙丙三位同学独立的解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为 、
、 、
、 , 则有人能够解决这个问题的概率为
, 则有人能够解决这个问题的概率为
 、
、 、
、 , 则有人能够解决这个问题的概率为
, 则有人能够解决这个问题的概率为
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知随机变量X服从二项分布B(n,p),若E(X)=40,D(X)=30,则p=
自主招生是高校在高考前争抢优等生的一项重要举措,不少同学也把自主招生当做高考前的一次锻炼,可谓是一层锻炼一层认识呀.据参加自主招生的某同学说,某高校2012自主招生选拔考试分为初试和面试两个阶段,参加面试的考生按照抽签方式决定出场顺序.通过初试,选拔出甲、乙等五名考生参加面试.
-
(1) 求面试中甲、乙两名考生恰好排在前两位的概率;
-
(2) 若面试中甲和乙之间间隔的考生数记为X,求X的分布列和数学期望.
一射手对同一目标独立地射击四次,已知至少命中一次的概率为  ,则此射手每次射击命中的概率为( )
,则此射手每次射击命中的概率为( )
 ,则此射手每次射击命中的概率为( )
,则此射手每次射击命中的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某人有4把钥匙,其中2把能打开门,现随机地取1把钥匙试着开门,不能开门的就扔掉,问第二次才能打开门的概率是;如果试过的钥匙不扔掉,这个概率是.
某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成.
-
(1) 求出甲考生正确完成题数的概率分布列,并计算数学期望;
-
(2) 若考生乙每题正确完成的概率都是
 ,且每题正确完成与否互不影响.试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
,且每题正确完成与否互不影响.试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
某中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,才能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
|
课 程 |
初等代数 |
初等几何 |
初等数论 |
微积分初步 |
|
合格的概率 |
| | | |
-
(1) 求甲同学取得参加数学竞赛复赛的资格的概率;
-
(2) 记
 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求  的分布列(只需列式无需计算)及期望
的分布列(只需列式无需计算)及期望  .
.
设  ,
,  ,
,  ,则
,则  的值分别为 ( )
的值分别为 ( )
 ,
,  ,
,  ,则
,则  的值分别为 ( )
的值分别为 ( )
A . 18,  B . 36,
B . 36,  C . 36,
C . 36,  D . 18,
D . 18, 
 B . 36,
B . 36,  C . 36,
C . 36,  D . 18,
D . 18, 
2019年春节期间,某超市举办了一次大型有奖促销活动,消费每超过800元(含800元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有12个形状、大小完全相同的小球(其中红球4个,黑球8个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
方案二:从装有12个形状、大小完全相同的小球(其中红球4个,黑球8个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受打5折优惠;若摸出2个红球则打6折,若摸出1个红球,则打8折;若没摸出红球,则不打折.
-
(1) 若两个顾客均消费了1100元,且均选择抽奖方案二,试求两位顾客均享受五折优惠的概率;
-
(2) 若某顾客消费1100元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
在一次“概率”相关的研究性活动中,老师在每个箱子中装了10个小球,其中9个是白球,1个是黑球,用两种方法让同学们来摸球.方法一:在20箱中各任意摸出一个小球;方法二:在10箱中各任意摸出两个小球.将方法一、二至少能摸出一个黑球的概率分别记为  和
和  ,则( )
,则( )
 和
和  ,则( )
,则( )
A .  B .
B .  C .
C .  D . 以上三种情况都有可能
D . 以上三种情况都有可能
 B .
B .  C .
C .  D . 以上三种情况都有可能
D . 以上三种情况都有可能
如图是某个闭合电路的一部分,每个元件的可靠性是  ,则从
,则从  到
到  这部分电路畅通的概率为( )
这部分电路畅通的概率为( )
 ,则从
,则从  到
到  这部分电路畅通的概率为( )
这部分电路畅通的概率为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
甲、乙两位同学独立地解答某道数学题,若甲、乙解出的概率都是  ,则这道数学题被解出的概率是( )
,则这道数学题被解出的概率是( )
 ,则这道数学题被解出的概率是( )
,则这道数学题被解出的概率是( )
A . 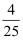 B .
B . 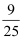 C .
C .  D .
D . 
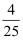 B .
B . 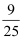 C .
C .  D .
D . 
《中共中央国务院关于实现巩固拓展脱贫攻坚成果同乡村振兴有效衔接的意见》明确提出,支持脱贫地区乡村特色产业发展壮大,加快脱贫地区农产品和食品仓储保鲜、冷链物流设施建设,支持农产品流通企业、电商、批发市场与区域特色产业精准对接.当前,脱贫地区相关设施建设情况如何?怎样实现精准对接?未来如何进一步补齐发展短板?针对上述问题,假定有A、B、C三个解决方案,通过调查发现有 的受调查者赞成方案A,有
的受调查者赞成方案A,有 的受调查者赞成方案B,有
的受调查者赞成方案B,有 的受调查者赞成方案C,现有甲、乙、丙三人独立参加投票(以频率作为概率).
的受调查者赞成方案C,现有甲、乙、丙三人独立参加投票(以频率作为概率).
 的受调查者赞成方案A,有
的受调查者赞成方案A,有 的受调查者赞成方案B,有
的受调查者赞成方案B,有 的受调查者赞成方案C,现有甲、乙、丙三人独立参加投票(以频率作为概率).
的受调查者赞成方案C,现有甲、乙、丙三人独立参加投票(以频率作为概率).
-
(1) 求甲、乙两人投票方案不同的概率;
-
(2) 若某人选择方案A或方案B,则对应方案可获得2票,选择方案C,则方案C获得1票,设
 是甲、乙、丙三人投票后三个方案获得票数之和,求
是甲、乙、丙三人投票后三个方案获得票数之和,求 的分布列和数学期望.
的分布列和数学期望.
新冠病毒是一种通过飞沫和接触传播的变异病毒,为筛查该病毒,有一种检验方式是检验血液样本相关指标是否为阳性,对于 份血液样本,有以下两种检验方式:一是逐份检验,则需检验
份血液样本,有以下两种检验方式:一是逐份检验,则需检验 次.二是混合检验,将其中
次.二是混合检验,将其中 份血液样本分别取样混合在一起,若检验结果为阴性,那么这
份血液样本分别取样混合在一起,若检验结果为阴性,那么这 份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这
份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这 份血液究竟哪些为阳性,就需要对它们再逐份检验,此时
份血液究竟哪些为阳性,就需要对它们再逐份检验,此时 份血液检验的次数总共为
份血液检验的次数总共为 次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为
次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为 .
.
 份血液样本,有以下两种检验方式:一是逐份检验,则需检验
份血液样本,有以下两种检验方式:一是逐份检验,则需检验 次.二是混合检验,将其中
次.二是混合检验,将其中 份血液样本分别取样混合在一起,若检验结果为阴性,那么这
份血液样本分别取样混合在一起,若检验结果为阴性,那么这 份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这
份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这 份血液究竟哪些为阳性,就需要对它们再逐份检验,此时
份血液究竟哪些为阳性,就需要对它们再逐份检验,此时 份血液检验的次数总共为
份血液检验的次数总共为 次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为
次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为 .
. (Ⅰ)求把2份血液样本混合检验结果为阳性的概率;
(Ⅱ)若检验次数的期望值越小,则方案越“优”.方案一、二、三中哪个最“优”?请说明理由.
已知随机变量 , 若
, 若 最大,则
最大,则 .
.
 , 若
, 若 最大,则
最大,则 .
.
投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏,在春秋战国时期较为盛行,假设甲、乙是唐朝的两位投壶游成参与者,且甲、乙每次投壶投中的概率分别为 、
、 若每人均投一次,则仅有一人投中的概率为;若每人均投壶3次,则甲比乙多投中2次的概率为.
若每人均投一次,则仅有一人投中的概率为;若每人均投壶3次,则甲比乙多投中2次的概率为.
 、
、 若每人均投一次,则仅有一人投中的概率为;若每人均投壶3次,则甲比乙多投中2次的概率为.
若每人均投一次,则仅有一人投中的概率为;若每人均投壶3次,则甲比乙多投中2次的概率为.
在甲,乙,丙三个地区爆发了流感,这三个地区分别有8%,6%,4%的人患了流感.若这三个地区的人口数的比为5:3:2,现从这三个地区中任意选取一个人,这个人患流感的概率是.
最近更新
- 我国坚持“引进来”与“走出去”相结合,全面提高对外开放水平,其根本目的是() A.参与国际经济技术合作与竞争 B.充分利
- 下列各组词语中,没有错别字的一组是 A.拖沓 娇生贯养 伶俐 倜傥不羁 B.造次 索然寡味 迁徙
- 一容器体积为V,其内气体压强为 P0.现用活塞式抽气机抽气,活塞筒的有效抽气容积为v=0.1 V,欲使容器内气体压强降为
- 2011年9月20日,《环球时报》刊发了采访文章《中国可进一步完善民族政策》,该文以“怎样看待少数民族政策”、“平等是最
- 倾倒液体药品时,标签向着手心,原因是____________________________。
- 计算:·= 。
- 依次填入下列各句横线处的词语,最恰当的一组是 ( )①开放性网络给人们交
- 最早规定美国总统由选举产生的文件是()A.《权利法案》 B.《人权宣言》C.《独立宣言》 D.1787年宪法
- 近年来幸福指数成为人们衡量一个城市发展的重要统计数据,但不同的人对幸福感的 诠释不同。某员工认为幸福就是工资再高点
- (2009湖北襄樊高三调研)依次填入下列横线处的词语,最恰当的一组是() (1)戛纳市位于法国东南部,______地中海
- The careless man received a ticket for speeding. He _____ ha
- 在我国失业保险制度还不健全的条件下,职工要保证自己的生活质量关键在于() A.国家要建立和完善社会保障制度 B.职工要转
- 读图,完成下列问题。(1)垃圾分类回收的好处是____________________。 (2)使用公共交通工具对生
- 下列组合正确的一组是( ) A.世界面积最广的雨林﹣﹣非洲 B.世界上最长的裂谷﹣﹣
- 下列各句中,标点符号使用正确的一句是( ) A.黄仁宇的《孔孟》一文选自《赫逊河畔谈中国历史》。(生活·读书·新知之
- 如图,已知抛物线,顶点记作.首先我们将抛物线关于直线对称翻折过去得到抛物线称为第一次操作,再将抛物线关于直线对称翻折过去
- 如图所示,轨道NO和OM底端对接且θ>α,小环自N点由静止滑下再滑上OM.已知小环在轨道NO下滑的距离小于在轨道OM上滑
- ---Has ______ English changed over time? --- “No”, he answ
- Ifyou’d listened to me, we ________the wrong way. A.
- 如图为周期表中短周期的一部分,若X原子最外层电子数比次外层电子数少3,则下列说法正确的是 ()R X Y Z





