4.1 二项分布 知识点题库
将一枚均匀的硬币投掷5次,则正面出现的次数比反面出现的次数多的概率( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
甲、乙两同学投篮进球的概率分别是 和
和 ,现甲、乙各投篮一次,都不进球的概率是( )
,现甲、乙各投篮一次,都不进球的概率是( )
 和
和 ,现甲、乙各投篮一次,都不进球的概率是( )
,现甲、乙各投篮一次,都不进球的概率是( )
A .  B .
B . 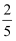 C .
C .  D .
D . 
 B .
B . 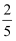 C .
C .  D .
D . 
某一批花生种子,如果每1粒发芽的概率为  ,那么播下4粒种子恰有2粒发芽的概率是.(请用分数表示结果)
,那么播下4粒种子恰有2粒发芽的概率是.(请用分数表示结果)
 ,那么播下4粒种子恰有2粒发芽的概率是.(请用分数表示结果)
,那么播下4粒种子恰有2粒发芽的概率是.(请用分数表示结果)
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是.

根据环保部门对某河流的每年污水排放量x(单位:吨)的历史统计数据,得到如下频率分布表:

将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
-
(1) 求在未来3年里,至多1年污水排放量
 的概率;
的概率;
-
(2) 该河流的污水排放对沿河的经济影响如下:当
 时,没有影响;当
时,没有影响;当  时,经济损失为10万元;当
时,经济损失为10万元;当  时,经济损失为60万元.为减少损失,现有三种应对方案:
时,经济损失为60万元.为减少损失,现有三种应对方案:方案一:防治350吨的污水排放,每年需要防治费3.8万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种文案,哪种方案好,并请说明理由.
某市政府为了节约生活用电,计划在本市试行居民生活费定额管理,即确定一户居民月用电量标准  ,用电量不超过
,用电量不超过  的部分按平价收费,超出
的部分按平价收费,超出  的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以
的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
 ,用电量不超过
,用电量不超过  的部分按平价收费,超出
的部分按平价收费,超出  的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以
的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
-
(1) 根据频率分布直方图的数据,求直方图中
 的值并估计该市每户居民平均用电量
的值并估计该市每户居民平均用电量 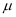 的值;
的值;
-
(2)
 用频率估计概率,利用(1)的结果,假设该市每户居民月平均用电量
用频率估计概率,利用(1)的结果,假设该市每户居民月平均用电量  服从正态分布
服从正态分布 
(i)估计该市居民月平均用电量介于
 度之间的概率;
度之间的概率;(ii)利用(i)的结论,从该市所有居民中随机抽取3户,记月平均用电量介于
 度之间的户数为
度之间的户数为  ,求
,求  的分布列及数学期望
的分布列及数学期望  .
.
某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
|
红球个数 |
3 |
2 |
1 |
0 |
|
实际付款 |
7折 |
8折 |
9折 |
原价 |
-
(1) 该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
-
(2) 若某顾客购物金额为180元,选择哪种方案更划算?
一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得-10分).
-
(1) 设每轮游戏中出现“摸出两个都是红球”的次数为X,求X的分布列;
-
(2) 玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
某校为了解学生一周的课外阅读情况,随机抽取了100名学生对其进行调查.下面是根据调查结果绘制的一周学生阅读时间(单位:分钟)的频率分布直方图,且将一周课外阅读时间不低于200分钟的学生称为“阅读爱好”,低于200分钟的学生称为“非阅读爱好”.

附:
| | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 .
.
-
(1) 根据已知条件完成下面
 列联表,并据此判断是否有97.5%的把握认为“阅读爱好”与性别有关?
列联表,并据此判断是否有97.5%的把握认为“阅读爱好”与性别有关? 非阅读爱好
阅读爱好
合计
男女
50
合计
14
男女
-
(2) 将频率视为概率,从该校学生中用随机抽样的方法抽取4人,记被抽取的四人中“阅读爱好”的人数为
 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求  的分布列和数学期望
的分布列和数学期望  .
.
一批产品的次品率为0.03,从这批产品中每次随机取一件,有放回地抽取100次,X表示抽到的次品件数,则  .
.
 .
.
若事件A与B相互独立,P(A)=  ,P(B)=
,P(B)=  ,则P(A∪B)=( )
,则P(A∪B)=( )
 ,P(B)=
,P(B)=  ,则P(A∪B)=( )
,则P(A∪B)=( )
A .  B .
B . 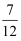 C .
C .  D .
D . 
 B .
B . 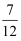 C .
C .  D .
D . 
运用计算机编程,设计一个将输入的正整数  “归零”的程序如下:按下回车键,等可能的将
“归零”的程序如下:按下回车键,等可能的将  中的任意一个整数替换
中的任意一个整数替换  的值并输出
的值并输出  的值,反复按回车键执行以上操作直到输出
的值,反复按回车键执行以上操作直到输出  后终止操作.
后终止操作.
 “归零”的程序如下:按下回车键,等可能的将
“归零”的程序如下:按下回车键,等可能的将  中的任意一个整数替换
中的任意一个整数替换  的值并输出
的值并输出  的值,反复按回车键执行以上操作直到输出
的值,反复按回车键执行以上操作直到输出  后终止操作.
后终止操作.
-
(1) 若输入的初始值
 为3,记按回车键的次数为
为3,记按回车键的次数为  ,求
,求  的概率分布与数学期望;
的概率分布与数学期望;
-
(2) 设输入的初始值为
 ,求运行“归零”程序中输出
,求运行“归零”程序中输出  的概率.
的概率.
投壸是从先秦延续至清末的汉民族传统礼仪和宴饮游戏,在春秋战国时期较为盛行.如图为一幅唐朝的投壶图,假设甲、乙是唐朝的两位投壶游戏参与者,且甲、乙每次投壶投中的概率分别为 , 每人每次投壸相互独立.若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的概率为( )
, 每人每次投壸相互独立.若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的概率为( )
 , 每人每次投壸相互独立.若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的概率为( )
, 每人每次投壸相互独立.若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
围棋起源于中国,据先秦典籍世本记载:“尧造围棋,丹朱善之”,至今已有四千多年历史围棋不仅能抒发意境、陶冶情操、修身养性、生慧增智,而且还与天象易理、兵法策略、治国安邦等相关联,蕴含着中华文化的丰富内涵在某次国际围棋比赛中,甲、乙两人进入最后决赛比赛采取五局三胜制,即先胜三局的一方获得比赛冠军,比赛结束假设每局比赛甲胜乙的概率都为 , 没有和局,且各局比赛的胜负互不影响,则甲在比赛中以
, 没有和局,且各局比赛的胜负互不影响,则甲在比赛中以 获得冠军的概率为( )
获得冠军的概率为( )
 , 没有和局,且各局比赛的胜负互不影响,则甲在比赛中以
, 没有和局,且各局比赛的胜负互不影响,则甲在比赛中以 获得冠军的概率为( )
获得冠军的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某商场为了促销规定顾客购买满500元商品即可抽奖,最多有3次抽奖机会.每次抽中,可依次获得10元,20元,30元奖金,若没有抽中,不可继续抽奖,顾客每次抽中后,可以选择带走所有奖金,结束抽奖;也可选择继续抽奖,若没有抽中,则连同前面所得奖金全部归零,结束抽奖.小明购买了500元商品并参与了抽奖活动,已知他每次抽中的概率依次为  ,
,  ,
,  ,选择继续抽奖的概率均为
,选择继续抽奖的概率均为  ,且每次是否抽中互不影响.
,且每次是否抽中互不影响.
 ,
,  ,
,  ,选择继续抽奖的概率均为
,选择继续抽奖的概率均为  ,且每次是否抽中互不影响.
,且每次是否抽中互不影响.
-
(1) 求小明第一次抽中,但所得奖金归零的概率;
-
(2) 设小明所得奖金总数为随机变量X,求X的分布列和数学期望.
为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了A,B两种小区管理方案,为了决定选取哪种方案为小区的最终管理方案,随机选取了4名物业人员进行投票,物业人员投票的规则如下:①单独投给A方案,则A方案得1分,B方案得-1分;②单独投给B方案,则B方案得1分,A方案得-1分;③弃权或同时投票给A,B方案,则两种方案均得0分.当前一名物业人员的投票结束,再安排下一名物业人员投票,当其中一种方案比另一种方案多4分或4名物业人员均已投票时,就停止投票,最后选取得分多的方案为小区的最终管理方案.假设A,B两种方案获得每一名物业人员投票的概率分别为 和
和 .
.
 和
和 .
.
-
(1) 在第一名物业人员投票结束后,A方案的得分记为
 , 求
, 求 的分布列;
的分布列;
-
(2) 求最终选取A方案为小区管理方案的概率.
某足球队在对球员的使用上进行数据分析,根据以往的数据统计,甲球员能够胜任前锋、中锋、后卫三个位置,且出场率分别为0.3,0.5,0.2,当甲球员在相应位置时,球队输球的概率依次为0.4,0.2,0.6.据此判断当甲球员参加比赛时,该球队某场比赛不输球的概率为;
北京2022年冬奥会吉祥物冰墩墩,作为北京冬奥会当之无愧的“顶流”,热度一直未减.自2022年冬奥会开始,一系列冰墩墩特许商品新品开始发售.根据百度网站统计:2022年1月28日至2022年2月22日购买冰墩墩人群分布图如下图.

-
(1) 求出频率分布直方图中购买者年龄的众数、平均数;(近似到个位数)
-
(2) 若将年龄
 分别记为A组、B组、C组,用随机抽样的方法从这些人抽取3人,求这三个人至少2人在A组的概率.
分别记为A组、B组、C组,用随机抽样的方法从这些人抽取3人,求这三个人至少2人在A组的概率.
某省会城市为了积极倡导市民优先乘坐公共交通工具绿色出行,切实改善城市空气质量,缓解城市交通压力,公共交通系统推出“2元换乘畅享公交”“定制公交”“限行日免费乘公交”“绿色出行日免费乘公交”等便民服务措施.为了更好地了解人们对出行工具的选择,交管部门随机抽取了1000人,做出如下统计表:
|
出行方式 |
步行 |
骑行 |
自驾 |
公共交通 |
|
比例 |
5% |
25% |
30% |
40% |
同时交管部门对某线路公交车统计整理了某一天1200名乘客的年龄数据,得到的频率分布直方图如图所示:

-
(1) 求m的值和这1200名乘客年龄的50%分位数;
-
(2) 用样本估计总体,将频率视为概率,从该市所有市民中抽取4人,记X为抽到选择公共交通出行方式的人数,求X的分布列和数学期望
 .
.
甲,乙两人进行围棋比赛,采取积分制,规则如下:每胜1局得1分,负1局或平局都不得分,积分先达到2分者获胜;若第四局结束,没有人积分达到2分,则积分多的一方获胜;若第四周结束,没有人积分达到2分,且积分相等,则比赛最终打平.假设在每局比赛中,甲胜的概率为 , 负的概率为
, 负的概率为 , 且每局比赛之间的胜负相互独立.
, 且每局比赛之间的胜负相互独立.
 , 负的概率为
, 负的概率为 , 且每局比赛之间的胜负相互独立.
, 且每局比赛之间的胜负相互独立.
-
(1) 求第三局结束时乙获胜的概率;
-
(2) 求甲获胜的概率.
最近更新
- 为防治荔枝蝽等植食性害虫,减少农药的使用,有人尝试在荔枝园的株间种植矮小的山绿豆。对比研究荔枝-山绿豆复合种植园和荔枝单
- 下列溶液中Cl-浓度与50 mL 1 mol·L-1AlCl3溶液中Cl-的物质的量浓度不相等的是 A.50 mL 3
- 有 CH3CH2OH、CH3CH2Br、NH4Cl溶液四种无色液体,只用一种试剂就能把它们鉴别开,这种试剂是() A.溴
- 阅读下面语段,在横线上填出与括号内词语意思相近的四字词语,不改变原句意思。 毕淑敏散文能通过色彩、声音、韵律、特定的语调
- 在箱子中装有10张卡片,分别写有1到10的10个整数.从箱子中任取1张卡片,记下它的读数x,然后再放回箱子中,第二次再从
- 20.a和b属于同一动物体内的两个细胞,通过对其DNA分子含量的测定,发现a细胞中DNA含量是b细胞的两倍,最可能的解释
- Our money is limited and we should for the next year.
- 孟德尔用纯种的黄色圆粒豌豆和纯种的绿色皱粒豌豆杂交,F1全部表现为黄色圆粒;F1代自交,在F2代中黄色圆粒、黄色皱粒、绿
- 《中共中央关于制定国民经济和社会发展第十二个五年规划的建议》是在中共中央领导下制定的。《建议》形成过程中,中共中央征求了
- 共价键、离子键和分子间作用力是物质间的不同作用力,下述物质中只含上述一种作用力的是( )A.干冰 B.氯化钠
- 如图所示,一正点电荷周围有A、B、C三点,其中B、C在同一个等势面上,有一个试探电荷q=-1.5×10-6C,则下列说法
- 下列对电磁学的发展起过决定意义的科学家是( ) A、伏特 B、奥斯特 C、法拉第 D、爱迪生
- . The thought worried him much ________ he might fail in the
- Not until all the fish died in the river ___ how serious the
- 阅读下面的内容,完成下面3题 北京:中轴线上的都城 “中国”的“中”字,是对于古代城市中轴线的最好的图示。从这个
- 张謇就任农商总长后说:“謇意自今为始,凡隶属本部(农商部)之官业,概行停罢.或予 掇商承办。惟择一、二大宗实业…为一私人
- 已知函数f(x)的图像与曲线C关于y轴对称,把曲线C沿x轴负方向平移一个单位恰好与函数y=|log2(-x-2)|的图像
- 若函数的导函数在区间上是增函数,则函数在区间上的图象可能是 y ( )
- 除去下列各物质中的少量杂质所选用的试剂及操作方法均正确的是( ▲ )项目 物质 杂质(少量) 试剂 操作方法 A KNO
- ......





