4.1 二项分布 知识点题库
将甲、乙等5名交警分配到三个不同路口疏导交通,每个路口至少一人,且甲、乙在同一路口的分配方案共有( )
A . 18种
B . 24种
C . 36种
D . 72种
某群体中的每位成员使用移动支付的概率都为  ,各成员的支付方式相互独立,设
,各成员的支付方式相互独立,设  为该群体的10位成员中使用移动支付的人数,
为该群体的10位成员中使用移动支付的人数,  则
则 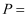 ( )
( )
 ,各成员的支付方式相互独立,设
,各成员的支付方式相互独立,设  为该群体的10位成员中使用移动支付的人数,
为该群体的10位成员中使用移动支付的人数,  则
则 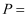 ( )
( )
A . 0.7
B . 0.6
C . 0.4
D . 0.3
随机变量  服从二项分布
服从二项分布  ,且
,且  ,则
,则  等于
等于
 服从二项分布
服从二项分布  ,且
,且  ,则
,则  等于
等于
A .  B .
B .  C . 1
D . 0
C . 1
D . 0
 B .
B .  C . 1
D . 0
C . 1
D . 0
某理财公司有两种理财产品  和
和  ,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
 和
和  ,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立): 产品 
| 投资结果 | 获利20% | 获利10% | 不赔不赚 | 亏损10% |
| 概率 | 0.2 | 0.3 | 0.2 | 0.3 |
产品  (其中
(其中  )
)
| 投资结果 | 获利30% | 不赔不赚 | 亏损20% |
| 概率 | | 0.1 | |
-
(1) 已知甲、乙两人分别选择了产品
 和产品
和产品  进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求
进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求  的取值范围;
的取值范围;
-
(2) 丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品
 和产品
和产品  之中选其一,应选用哪种产品?
之中选其一,应选用哪种产品?
将一颗质地均匀的骰子先后抛掷3次,至少出现一次6点向上的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
2019国际乒联世界巡回赛男子单打决赛在甲、乙两位选手间进行,比赛实行七局四胜制(先获得四局胜利的选手获胜),已知每局比赛甲选手获胜的概率是  ,且前五局比赛甲
,且前五局比赛甲  领先,则甲获得冠军的概率是.
领先,则甲获得冠军的概率是.
 ,且前五局比赛甲
,且前五局比赛甲  领先,则甲获得冠军的概率是.
领先,则甲获得冠军的概率是.
过去五年,我国的扶贫工作进入了“精准扶贫”阶段.目前“精准扶贫”覆盖了全部贫困人口,东部帮西部,全国一盘棋的扶贫格局逐渐形成.到2020年底全国830个贫困县都将脱贫摘帽,最后4335万贫困人口将全部脱贫,这将超过全球其他国家过去30年脱贫人口总和.2020年是我国打赢脱贫攻坚战收官之年,越是到关键时刻,更应该强调“精准”.为落实“精准扶贫”政策,某扶贫小组,为一“对点帮扶”农户引种了一种新的经济农作物,并指导该农户于2020年初开始种植.已知该经济农作物每年每亩的种植成本为1000元,根据前期各方面调查发现,该经济农作物的市场价格和亩产量均具有随机性,且两者互不影响,其具体情况如下表:
|
该经济农作物亩产量(kg) |
900 |
1200 |
该经济农作物市场价格(元/kg) |
15 |
20 |
|
|
概率 |
0.5 |
0.5 |
概率 |
0.4 |
0.6 |
-
(1) 设2020年该农户种植该经济农作物一亩的纯收入为X元,求X的分布列;
-
(2) 若该农户从2020年开始,连续三年种植该经济农作物,假设三年内各方面条件基本不变,求这三年中该农户种植该经济农作物一亩至少有两年的纯收入不少于16000元的概率;
-
(3) 2020年全国脱贫标准约为人均纯收入4000元.假设该农户是一个四口之家,且该农户在2020年的家庭所有支出与其他收入正好相抵,能否凭这一亩经济农作物的纯收入,预测该农户在2020年底可以脱贫?并说明理由.
甲、乙两人独立地对同一目标各射击一次,命中率分别为0.6和0.7,在目标被击中的情况下,甲、乙同时击中目标的概率为( )
A .  B .
B .  C .
C .  D .
D . 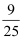
 B .
B .  C .
C .  D .
D . 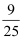
某学校高二年级有2000名学生进行了一次物理测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生作为样本,记录他们的成绩数据,将数据分成7组:[30,40),[40,50),…[90,100],整理得到如图频率分布直方图.

-
(1) 若该样本中男生有60人,试估计该学校高二年级女生总人数;
-
(2) 根据频率分布直方图,求样本中物理成绩在[70,90)的频率;
-
(3) 用频率估计概率,现从该校高二年级学生中随机抽取2人,求恰有一名学生的物理成绩在[70,90)的概率.
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
|
日均浓度 | | | | | | |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:

(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.每局比赛甲队获胜的概率是  ,没有平局.假设各局比赛结果互相独立.甲队以3:2胜利的概率是( )
,没有平局.假设各局比赛结果互相独立.甲队以3:2胜利的概率是( )
 ,没有平局.假设各局比赛结果互相独立.甲队以3:2胜利的概率是( )
,没有平局.假设各局比赛结果互相独立.甲队以3:2胜利的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某批种子,如果每粒种子的发芽概率是 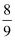 ,则播下5粒种子恰有3粒发芽的概率为.
,则播下5粒种子恰有3粒发芽的概率为.
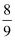 ,则播下5粒种子恰有3粒发芽的概率为.
,则播下5粒种子恰有3粒发芽的概率为.
甲、乙两队进行友谊赛,采取三局两胜制,每局都要分出胜负,根据以往经验,单局比赛中甲队获胜的概率为  ,设各局比赛相互间没有影响,则甲队战胜乙队的概率为( )
,设各局比赛相互间没有影响,则甲队战胜乙队的概率为( )
 ,设各局比赛相互间没有影响,则甲队战胜乙队的概率为( )
,设各局比赛相互间没有影响,则甲队战胜乙队的概率为( )
A . 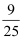 B .
B .  C .
C .  D .
D . 
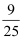 B .
B .  C .
C .  D .
D . 
已知随机变量  ,则
,则  .
.
 ,则
,则  .
.
设随机变量  ,且
,且  ,则
,则  .
.
 ,且
,且  ,则
,则  .
.
在一个坛子中装有16个除颜色之外完全相同的玻璃球,其中有2个红的,3个蓝的,5个绿的,6个黄的,从中任取一球,放回后,再取一球,则第一次取出红球且第二次取出黄球的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
为充分感受冬奥的运动激情,领略奥运的拼搏精神,甲、乙、丙三人进行短道速滑训练.已知每一场比赛甲、乙、丙获胜的概率分别为 ,
,  ,
,  , 则3场训练赛过后,甲、乙获胜场数相同的概率为( )
, 则3场训练赛过后,甲、乙获胜场数相同的概率为( )
 ,
,  ,
,  , 则3场训练赛过后,甲、乙获胜场数相同的概率为( )
, 则3场训练赛过后,甲、乙获胜场数相同的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
进入2021年以来,大学生学理财成为一种新的趋势,已知年初小赵买进某个理财产品,设该产品每年收益率为 , 根据历史数据可知,
, 根据历史数据可知, , 则小赵在大学期间投资该产品4年,至少有2年收益为正的概率为.
, 则小赵在大学期间投资该产品4年,至少有2年收益为正的概率为.
 , 根据历史数据可知,
, 根据历史数据可知, , 则小赵在大学期间投资该产品4年,至少有2年收益为正的概率为.
, 则小赵在大学期间投资该产品4年,至少有2年收益为正的概率为.
甲、乙两人每次投篮命中的概率分别 , 甲、乙两人投中与否互不影响.现若两人各投篮一次,则至少有一人命中的概率为;若每人投篮两次,两人共投中三次的概率为.
, 甲、乙两人投中与否互不影响.现若两人各投篮一次,则至少有一人命中的概率为;若每人投篮两次,两人共投中三次的概率为.
 , 甲、乙两人投中与否互不影响.现若两人各投篮一次,则至少有一人命中的概率为;若每人投篮两次,两人共投中三次的概率为.
, 甲、乙两人投中与否互不影响.现若两人各投篮一次,则至少有一人命中的概率为;若每人投篮两次,两人共投中三次的概率为.
某大型工厂有5台大型机器,在1个月中,1台机器至多出现 次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修.每台机器出现故障的概率为
次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修.每台机器出现故障的概率为 . 已知1名工人每月只有维修1台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得10万元的利润,否则将亏损3万元.该工厂每月需支付给每名维修工人1.5万元的工资.
. 已知1名工人每月只有维修1台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得10万元的利润,否则将亏损3万元.该工厂每月需支付给每名维修工人1.5万元的工资.
 次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修.每台机器出现故障的概率为
次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修.每台机器出现故障的概率为 . 已知1名工人每月只有维修1台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得10万元的利润,否则将亏损3万元.该工厂每月需支付给每名维修工人1.5万元的工资.
. 已知1名工人每月只有维修1台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得10万元的利润,否则将亏损3万元.该工厂每月需支付给每名维修工人1.5万元的工资.
-
(1) 若每台机器在当月不出现故障或出现故障时有工人进行维修,则称工厂能正常运行.若该厂只有2名维修工人,求工厂每月能正常运行的概率;
-
(2) 已知该厂现有4名维修工人.
(ⅰ)记该厂每月获利为
 万元,求
万元,求 的分布列与数学期望;
的分布列与数学期望;(ⅱ)以工厂每月获利的数学期望为决策依据,试问该厂是否应再招聘1名维修工人?
最近更新
- ---Jim isn’t in the classroom. Where is he?--- He ____ to th
- 学习光学知识后,小科对有关实验进行了思考和创新:(1)在如图所示的“探究平面镜成像规律”实验中,小科用玻璃板代替平面镜来
- 读图18“我国环境问题分布示意图”,完成下列要求。(1)将下列地区面临的主要环境问题填在相应地区后的括号里(填字母):
- 下列词语没有错别字的一项是 A.静穆 羸弱 步履 变幻多姿 B.遮蔽 协奏 崔嵬 迫不急待 C.疆域
- 如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是() A.12π B.11πC.10π D.
- 若以图甲代表与生命系统相关概念的范围,其中正确的是 ( ) 供选项 a b c A 生物大分子 细
- Polar bears live mostly on ________ sea ice, which they use
- 显微镜是生物实验中重要的观察工具,下列关于显微镜的说法错误的是 A.调节粗准焦螺旋和细准焦螺旋都能使镜筒上升或下降 B.
- “蝴蝶效应”由气象学家洛伦兹于1963年提出,其大意是:南美洲亚马孙河流域热带雨林中的一只蝴蝶,偶尔扇动几下翅膀,可能在
- 如图,AB = AD,CB = CD. 求证:∠B =∠D.
- 如图2-1-19,空间四边形ABCD中,AB=AD=2,BC=DC=1,AD和BC所成角为60°,E、F分别为AB、CD
- 下列句式不同于其他三句的是( ) A、蚓无爪牙之利,筋骨之强 B、虽有槁暴,不复
- 植物的光合作用和呼吸作用都要受到外界环境因素的影响,下图所示有关曲线表示正确的是()
- 下图是《 科学》 教材中的几个实验,其中图文描述不一致的是A.磁极间相互作用 B.铁棒被磁化 C.通电导体周围存
- 如图,将一张边长为6cm的正方形纸片按虚线裁剪后,恰好围成底面是正六边形的棱柱,则这个六棱柱的侧面积为cm2.
- 下列说法正确的是 ▲ A.黑体辐射电磁波的强度按波长的分布只与黑体的温度有关 B.粒子散射实验说明原子核是有内部结
- 阅读下面文字,完成1—3题。 纺 车 万方 人类区别于动物的特征之一,便是能以衣着保暖和遮羞。制衣不能离开纺织
- A very large gymnasium(体育馆) is under c________________ in ou
- 解方程:(-1)(+1)x=4-2(x+2).
- 科学家从烟草花叶病毒(TMV)中分离出a、b两个不同品系,它们感染植物产生的病斑形态不同。下列4组实验(见下表)中,不可











