4.1 二项分布 知识点题库
位于坐标原点的一个质点P,其移动规则是:质点每次移动一个单位,移动的方向向上或向右,并且向上、向右移动的概率都是 . 质点P移动5次后位于点(2,3)的概率是( )
. 质点P移动5次后位于点(2,3)的概率是( )
 . 质点P移动5次后位于点(2,3)的概率是( )
. 质点P移动5次后位于点(2,3)的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
随机变量 服从二项分布
服从二项分布 ~
~ , 且
, 且 则
则 等于( )
等于( )
 服从二项分布
服从二项分布 ~
~ , 且
, 且 则
则 等于( )
等于( )
A . 4
B . 12
C . 4或12
D . 3
化简逻辑函数式A +B
+B +BC+AB=
+BC+AB=
 +B
+B +BC+AB=
+BC+AB=
以下是新兵训练时,某炮兵连8周中炮弹对同一目标的命中情况的柱状图:

-
(1) 计算该炮兵连这8周中总的命中频率p0 , 并确定第几周的命中频率最高;
-
(2) 以(1)中的p0作为该炮兵连炮兵甲对同一目标的命中率,若每次发射相互独立,且炮兵甲发射3次,记命中的次数为X,求X的数学期望;
-
(3) 以(1)中的p0作为该炮兵连炮兵对同一目标的命中率,试问至少要用多少枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99?(取lg0.4=﹣0.398)
已知随机变量X服从二项分布B(n,p),若E(X)=30,D(X)=20,则n,p分别等于( )
A . n=45,p=  B . n=45,p=
B . n=45,p=  C . n=90,p=
C . n=90,p=  D . n=90,p=
D . n=90,p= 
 B . n=45,p=
B . n=45,p=  C . n=90,p=
C . n=90,p=  D . n=90,p=
D . n=90,p= 
为有效预防新冠肺炎对老年人的侵害,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,根据测试成绩(百分制)绘制茎叶图如下.根据老年人体质健康标准,可知成绩不低于80分为优良,且体质优良的老年人感染新冠肺炎的可能性较低.

(Ⅰ)从抽取的12人中随机选取3人,记  表示成绩优良的人数,求
表示成绩优良的人数,求  的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)将频率视为概率,根据用样本估计总体的思想,在该社区全体老年人中依次抽取10人,若抽到  人的成绩是优良的可能性最大,求
人的成绩是优良的可能性最大,求  的值.
的值.
在某次考试中,甲、乙通过的概率分别为0.7,0.4,若两人考试相互独立,则甲未通过而乙通过的概率为( )
A . 0.28
B . 0.12
C . 0.42
D . 0.16
新冠肺炎病毒可以通过飞沫传染,佩戴口罩可以预防新冠肺炎病毒传染,已知  三人与新冠肺炎病人甲近距离接触,由于
三人与新冠肺炎病人甲近距离接触,由于  三人都佩戴了某种类型的口罩,若佩戴了该种类型的口罩,近距离接触病人被感染的概率为
三人都佩戴了某种类型的口罩,若佩戴了该种类型的口罩,近距离接触病人被感染的概率为  ,记
,记  三人中被感染的人数为X,则X的数学期望
三人中被感染的人数为X,则X的数学期望  ( )
( )
 三人与新冠肺炎病人甲近距离接触,由于
三人与新冠肺炎病人甲近距离接触,由于  三人都佩戴了某种类型的口罩,若佩戴了该种类型的口罩,近距离接触病人被感染的概率为
三人都佩戴了某种类型的口罩,若佩戴了该种类型的口罩,近距离接触病人被感染的概率为  ,记
,记  三人中被感染的人数为X,则X的数学期望
三人中被感染的人数为X,则X的数学期望  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设随机变量  ,则
,则  .
.
 ,则
,则  .
.
已知甲每次投篮命中率是0.8,乙每次投篮命中率是0.6,且各次投篮互不影响.
-
(1) 求甲投篮3次,投中2次的概率;
-
(2) 若甲和乙轮流投篮,每人每次投1球,约定甲先投篮,且先投中者获胜,一直到有人获胜或者每人都已投球3次时投篮结束.设投篮结束时,乙投球的次数为X,求P(X=0),P(X≥2).
甲、乙两人进行羽毛球单打比赛,根据以往比赛的胜负情况知道,每一局甲获胜的概率为  ,乙获胜的概率为
,乙获胜的概率为  ,如果比赛采用“三局二胜”制(先胜二局者获胜),则前两局打平且甲获胜的概率为.
,如果比赛采用“三局二胜”制(先胜二局者获胜),则前两局打平且甲获胜的概率为.
 ,乙获胜的概率为
,乙获胜的概率为  ,如果比赛采用“三局二胜”制(先胜二局者获胜),则前两局打平且甲获胜的概率为.
,如果比赛采用“三局二胜”制(先胜二局者获胜),则前两局打平且甲获胜的概率为.
已知甲、乙两名运动员试跳某个高度成功的概率分别是0.7、0.6,且每次试跳成功与否之间互不影响.
-
(1) 求甲试跳两次,两次均成功的概率;
-
(2) 求甲、乙两人在一次试跳中,至少有一人成功的概率.
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
-
(1) 若厂家库房中(视为数量足够多)的每件产品合格的概率为0.7,从中任意取出3件进行检验,求至少有2件是合格品的概率;
-
(2) 若厂家发给商家20件产品,其中有4件不合格,按合同规定商家从这20件产品中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.
①求该商家可能检验出的不合格产品的件数X的分布列和数学期望;
②求该商家拒收这批产品的概率.
十三届全国人大四次会议表决通过了关于国民经济和社会发展第十四个五年规划和2035年远景目标纲要的决议,决定批准这个规划纲要,纲要指出:“加强原创性引领性科技攻关”.某企业集中科研骨干,攻克系列“卡脖子”技术,已成功实现离子注入机全谱系产品国产化,包括中束流、大束流、高能、特种应用及第三代半导体等离子注入机,工艺段覆盖至28nm,为我国芯片制造产业链补上重要一环,为全球芯片制造企业提供离子注入机一站式解决方案.此次技术的突破可以说为国产芯片的制造做出了重大贡献.该企业使用新技术对某款芯片进行试生产,在试产初期,生产一件该款芯片有三道工序,每道工序的生产互不影响,这三道工序的次品率分别为 ,
,  ,
,  .
.
 ,
,  ,
,  .
. 附: ,
,  .
.
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
-
(1) ①求生产一件该芯片的次品率
 .
. ②试产100件该芯片,估计次品件数
 的期望.
的期望. -
(2) 某手机生产厂商将该款芯片投入到某新款手机上使用,并对部分芯片做了技术改良,推出了两种型号的手机,甲型号手机采用没有改良的芯片,乙型号手机采用改良了的芯片,现对使用这两种型号的手机用户进行回访,就他们对开机速度进行满意度调查.据统计,回访的100名用户中,使用甲型号手机的有30人,其中对开机速度满意的有15人;使用乙型号手机的有70人,其中对开机速度满意的有55人.完成下列
 列联表,并判断是否有99.5%的把握认为该项技术改良与用户对开机速度的满意度有关.
列联表,并判断是否有99.5%的把握认为该项技术改良与用户对开机速度的满意度有关.甲型号
乙型号
合计
满意
不满意
合计
猜灯谜又称打灯谜,是我国从古代就开始流传的元宵节特色活动.在一次元宵节猜灯谜活动中,共有20道灯谜,三位同学独立竞猜,甲同学猜对了12道,乙同学猜对了8道,丙同学猜对了 道.假设每道灯谜被猜对的可能性都相等.
道.假设每道灯谜被猜对的可能性都相等.
 道.假设每道灯谜被猜对的可能性都相等.
道.假设每道灯谜被猜对的可能性都相等.
-
(1) 任选一道灯谜,求甲,乙两位同学恰有一个人猜对的概率;
-
(2) 任选一道灯谜,若甲,乙,丙三个人中至少有一个人猜对的概率为
 , 求
, 求 的值.
的值.
2022年,是中国共产主义青年团成立100周年,为引导和带动青少年重温共青团百年光辉历程,某校组织全体学生参加共青团百年历史知识竞赛,现从中随机抽取了100名学生的成绩组成样本,并将得分分成以下6组:[40,50)、[50,60)、[60,70)、 、[90,100],统计结果如图所示:
、[90,100],统计结果如图所示:
 、[90,100],统计结果如图所示:
、[90,100],统计结果如图所示:
-
(1) 试估计这100名学生得分的平均数(同一组中的数据用该组区间中点值代表);
-
(2) 试估计这100名学生得分的中位数(结果保留两位小数);
-
(3) 现在按分层抽样的方法在[80,90)和[90,100]两组中抽取5人,再从这5人中随机抽取2人参加这次竞赛的交流会,试求两组各有一人被抽取的概率.
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.7,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
-
(1) 求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
-
(2) 求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率.
制造一种零件,甲机床的正品率为0.9,乙机床的正品率为0.8.从它们制造的产品中各任抽1件,则两件都是正品的概率是.
已知随机变量X服从二项分布X~B  ,则P(X=2)=( )
,则P(X=2)=( )
 ,则P(X=2)=( )
,则P(X=2)=( )
A .  B .
B .  C .
C . 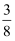 D .
D . 
 B .
B .  C .
C . 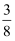 D .
D . 
某品牌电脑售后保修期为一年,根据1000台电脑的维修记录资料(保修期内所有电脑维修次数均不超2次),这1000台电脑在保修期内需要维修1次的有300台,需要维修2次的占20%.以这1000台电脑维修次数的频率代替1台电脑维修次数的概率.
-
(1) 求1台电脑保修期内不需要维修的概率;
-
(2) 若某人购买2台这个品牌的电脑,2台电脑在保修期内是否需要维修互不影响,如果2台电脑保修期内需要维修的次数总和不超过2次的概率大于0.8,则认为该品牌电脑“值得信赖”,请判断该品牌电脑是否“值得信赖”,并说明理由.
最近更新
- 已知m是方程x2-x-1=0的一个根,则代数式m2-m的值为() A.-1B.0C.1D.2
- —What will you donate for the charity? —I’ll ________ some c
- 读下面这首诗,完成①—③题。 送魏万之京 李颀 朝闻游子唱离歌,昨夜微霜初渡河。 鸿雁不堪愁里听,云山况是客中过。 关
- 家蚕是二倍体,体细胞中有28对染色体,其中一对是性染色体,雄蚕含有两个同型的性染色体ZZ,雌蚕含有两个异型的性染色体ZW
- 在2FeBr2+3Cl22FeCl3+2Br2的反应中,被氧化的元素是() A.Fe B.Br C.Fe和Br D.Cl
- 2010年中央农村工作会议指出,要继续深化集体林权制度改革,继续推进草原基本经营制度改革。材料体现的唯物史观道理是 A.
- Onlyin this way _______remember the day _______we first met
- 卢瑟福提出了原子的核式结构模型,这一模型建立的基础是(A)粒子的散射实验 (B)
- Great efforts to increase grain production if food sho
- 如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B。现给B一个沿垂直AB方向的速度v0,
- 元素的性质随着原子序数的递增呈现周期性变化的根本原因是 A.元素相对原子质量的递增,量变引起质变 B.元素的
- 羟基水杨胺(Z)可以治疗胆囊炎、胆管炎等。合成羟苯水杨胺的反应如下图,下列说法正确的是 A. X能和NaHCO3溶
- 亚洲战争策源地形成的标志是:( )A.“九一八”事变 B.“二二六”兵变C
- 18.阅读下面的材料,按要求写一篇不少于800字的文章。(60分) 袁苏妹,学历,没有读过小学,除了自己的姓名,她当时还
- 将一定量的化学式为xFeSO4•y(NH4)2SO4.6H2O的晶体加入到过量的NaOH溶液中加热,得到NH3 0.85
- The managers discussed the plan that they would like to see
- 已知芦花鸡基因B在性染色体上,对非芦花鸡基因b是显性,为了尽早而准确地知道小鸡的性别,应选用() A.非芦花母鸡和芦花公
- 如图5所示,将物体A放在容器B中,以某一速度把容器B竖直上抛,不计空气阻力,运动过程中容器B的地面始终保持水平,下列说法
- (10分)如图所示,在竖直方向上A、B物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上,B、C两物体通过细绳绕过轻质
- 一木块静置于光滑水平面上,一颗子弹沿水平方向飞来射入木块中。当子弹进入木块的深度达到最大值3.0cm时,木块沿水平面恰好




