4.1 二项分布 知识点题库
甲从学校乘车回家,途中有3个交通岗,假设在各交通岗遇红灯的事件是相互独立的,并且概率都是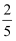 , 则甲回家途中遇红灯次数的期望为( )
, 则甲回家途中遇红灯次数的期望为( )
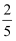 , 则甲回家途中遇红灯次数的期望为( )
, 则甲回家途中遇红灯次数的期望为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
现有4个人去参加娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ.
某人有5把钥匙,其中只有一把可以打开房门,他随意地进行试开,若试过的钥匙放在一旁,打开门时试过的次数ξ为随机变量,则P(ξ=3)等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某居民小区有  三个相互独立的消防通道,通道
三个相互独立的消防通道,通道  在任意时刻畅通的概率分别为
在任意时刻畅通的概率分别为  .
.
 三个相互独立的消防通道,通道
三个相互独立的消防通道,通道  在任意时刻畅通的概率分别为
在任意时刻畅通的概率分别为  .
.
-
(1) 求在任意时刻至少有两个消防通道畅通的概率;
-
(2) 在对消防通道
 的三次相互独立的检查中,记畅通的次数为随机变量
的三次相互独立的检查中,记畅通的次数为随机变量  ,求
,求  的分布列和数学期望
的分布列和数学期望  .
.
设事件A在每次试验中发生的概率相同,且在三次独立重复试验中,若事件A至少发生一次的概率为  ,则事件A恰好发生一次的概率为.
,则事件A恰好发生一次的概率为.
 ,则事件A恰好发生一次的概率为.
,则事件A恰好发生一次的概率为.
设  ,其中
,其中  ,且
,且  ,则
,则  ( )
( )
 ,其中
,其中  ,且
,且  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
据相关部门统计,随着电商网购的快速普及,快递包装业近年来实现了超过50%的高速年均增长,针对这种大好形式,某化工厂引进了一条年产量为1000万个包装胶带的生产线.已知该包装胶带的质量以某项指标值  为衡量标准.为估算其经济效益,该化工厂先进行了试生产,并从中随机抽取了1000个包装胶带,统计了每个包装胶带的质量指标值k,并分成以下5组,其统计结果及产品等级划分如下表所示:
为衡量标准.为估算其经济效益,该化工厂先进行了试生产,并从中随机抽取了1000个包装胶带,统计了每个包装胶带的质量指标值k,并分成以下5组,其统计结果及产品等级划分如下表所示:
 为衡量标准.为估算其经济效益,该化工厂先进行了试生产,并从中随机抽取了1000个包装胶带,统计了每个包装胶带的质量指标值k,并分成以下5组,其统计结果及产品等级划分如下表所示:
为衡量标准.为估算其经济效益,该化工厂先进行了试生产,并从中随机抽取了1000个包装胶带,统计了每个包装胶带的质量指标值k,并分成以下5组,其统计结果及产品等级划分如下表所示: | 质量指标 | | | | | |
| 产品等级 | | | | | 废品 |
| 频数 | 160 | 300 | 400 | 100 | 40 |
试利用该样本的频率分布估计总体的概率分布,并解决下列问题(注:每组数据取区间的中点值).
参考数据:若随机变量  ,则
,则  ,
,  ,
,  ,
,  ,
,  .
.
-
(1) 由频数分布表可认为,该包装胶带的质量指标值
 近似地服从正态分布
近似地服从正态分布  ,其中
,其中 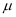 近似为样本平均数
近似为样本平均数  ,
,  近似为样本的标准差
近似为样本的标准差  ,并已求得
,并已求得  .记
.记  表示某天从生产线上随机抽取的30个包装胶带中质量指标值
表示某天从生产线上随机抽取的30个包装胶带中质量指标值  在区间
在区间  之外的包装胶带个数,求
之外的包装胶带个数,求  及
及  的数学期望(精确到0.001);
的数学期望(精确到0.001);
-
(2) 已知每个包装胶带的质量指标值
 与利润
与利润  (单位:元)的关系如下表所示:
(单位:元)的关系如下表所示:  .
. 质量指标






利润






假定该化工厂所生产的包装胶带都能销售出去,且这一年的总投资为5000万元(含引进生产线、兴建厂房等等一切费用在内),问:该化工厂能否在一年之内通过生产包装胶带收回投资?试说明理由.
某学校为了了解学生对新冠病毒的传播和预防知识的掌握情况,学校决定组织一次有关新冠病毒预防知识竞答.竞答分为必答题(共5题)和选答题(共2题)两部分.每位同学答题相互独立,且每道题答对与否互不影响.已知甲同学答对每道必答题的概率为  ,答对每道选答题的概率为
,答对每道选答题的概率为  .
.
 ,答对每道选答题的概率为
,答对每道选答题的概率为  .
.
-
(1) 求甲恰好答对4道必答题的概率;
-
(2) 在选答阶段,若选择回答且答对奖励5分,答错扣2分,选择放弃回答得0分.已知甲同学对于选答的两道题,选择回答和放弃回答的概率均为
 ,试求甲同学在选答题阶段,得分
,试求甲同学在选答题阶段,得分  的分布列.
的分布列.
若A,B互为对立事件,其概率分别为P(A)=  ,P(B)=
,P(B)=  ,且x>0,y>0,则x+y的最小值为.
,且x>0,y>0,则x+y的最小值为.
 ,P(B)=
,P(B)=  ,且x>0,y>0,则x+y的最小值为.
,且x>0,y>0,则x+y的最小值为.
某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.规则如下:从大小形状完全相同的4个红球6个白球的甲箱中摸取2个球,若摸中2个白球,获纪念奖10元;若摸中1个白球和1个红球,则获二等奖20元;若摸中2个红球,则获一等奖50元.
-
(1) 某顾客参与一次抽奖获得奖金金额为
 元,求
元,求  的分布列和期望;
的分布列和期望;
-
(2) 若某顾客有3次抽奖机会,求该顾客获得总奖金不少于50元的概率.
某商城玩具柜台元旦期间促销,购买甲、乙系列的盲盒,并且集齐所有的产品就可以赠送元旦礼品.而每个甲系列盲盒可以开出玩偶  ,
,  ,
,  中的一个,每个乙系列盲盒可以开出玩偶
中的一个,每个乙系列盲盒可以开出玩偶 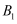 ,
,  中的一个.
中的一个.
 ,
,  ,
,  中的一个,每个乙系列盲盒可以开出玩偶
中的一个,每个乙系列盲盒可以开出玩偶 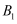 ,
,  中的一个.
中的一个.
-
(1) 记事件
 :一次性购买
:一次性购买  个甲系列盲盒后集齐
个甲系列盲盒后集齐  ,
,  ,
,  玩偶;事件
玩偶;事件  :一次性购买
:一次性购买  个乙系列盲盒后集齐
个乙系列盲盒后集齐 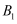 ,
,  玩偶;求概率
玩偶;求概率  及
及  ;
;
-
(2) 礼品店限量出售甲、乙两个系列的盲盒,每个消费者每天只有一次购买机会,且购买时,只能选择其中一个系列的一个盲盒.通过统计发现:第一次购买盲盒的消费者购买甲系列的概率为
 ,购买乙系列的概率为
,购买乙系列的概率为  ;而前一次购买甲系列的消费者下一次购买甲系列的概率为
;而前一次购买甲系列的消费者下一次购买甲系列的概率为  ,购买乙系列的概率为
,购买乙系列的概率为  ;前一次购买乙系列的消费者下一次购买甲系列的概率为
;前一次购买乙系列的消费者下一次购买甲系列的概率为  ,购买乙系列的概率为
,购买乙系列的概率为  ;如此往复,记某人第
;如此往复,记某人第  次购买甲系列的概率为
次购买甲系列的概率为  .
. ①
 ;
;②若每天购买盲盒的人数约为100,且这100人都已购买过很多次这两个系列的盲盒,试估计该礼品店每天应准备甲、乙两个系列的盲盒各多少个.
我国抗疫期间,素有“南抖音,北快手”之说的小视频除了给人们带来生活中的快乐外,更在于传递了一种正能量,为抗疫起到了积极的作用,但一个优秀的作品除了需要有很好的素材外,更要有制作上的技术要求,某同学学习利用“快影”软件将已拍摄的素材进行制作,每次制作分三个环节来进行,其中每个环节制作合格的概率分别为  ,
,  ,
,  ,只有当每个环节制作都合格才认为一次成功制作,该小视频视为合格作品.该同学进行3次制作,恰有一次合格作品的概率为(用数字作答).
,只有当每个环节制作都合格才认为一次成功制作,该小视频视为合格作品.该同学进行3次制作,恰有一次合格作品的概率为(用数字作答).
 ,
,  ,
,  ,只有当每个环节制作都合格才认为一次成功制作,该小视频视为合格作品.该同学进行3次制作,恰有一次合格作品的概率为(用数字作答).
,只有当每个环节制作都合格才认为一次成功制作,该小视频视为合格作品.该同学进行3次制作,恰有一次合格作品的概率为(用数字作答).
设随机变量  ,记
,记  .在研究
.在研究  的最大值时,某数学兴趣小组的同学发现:若
的最大值时,某数学兴趣小组的同学发现:若  为正整数,则
为正整数,则  时,
时,  ,此时这两项概率均为最大值;若
,此时这两项概率均为最大值;若  为非整数,当
为非整数,当  取
取  的整数部分,则
的整数部分,则  是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的股子并实时记录点数1出现的次数.当投郑到第30次时,记录到此时点数1出现7次,若继续再进行70次投掷试验,则当投掷到第100次时,点数1总共出现的次数为( )的概率最大
是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的股子并实时记录点数1出现的次数.当投郑到第30次时,记录到此时点数1出现7次,若继续再进行70次投掷试验,则当投掷到第100次时,点数1总共出现的次数为( )的概率最大
 ,记
,记  .在研究
.在研究  的最大值时,某数学兴趣小组的同学发现:若
的最大值时,某数学兴趣小组的同学发现:若  为正整数,则
为正整数,则  时,
时,  ,此时这两项概率均为最大值;若
,此时这两项概率均为最大值;若  为非整数,当
为非整数,当  取
取  的整数部分,则
的整数部分,则  是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的股子并实时记录点数1出现的次数.当投郑到第30次时,记录到此时点数1出现7次,若继续再进行70次投掷试验,则当投掷到第100次时,点数1总共出现的次数为( )的概率最大
是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的股子并实时记录点数1出现的次数.当投郑到第30次时,记录到此时点数1出现7次,若继续再进行70次投掷试验,则当投掷到第100次时,点数1总共出现的次数为( )的概率最大
A . 16
B . 17
C . 18
D . 19
在4次独立重复试验中,事件A发生的概率相同,若事件A至少发生1次的概率为  ,则事件A在一次试验中发生的概率为( )
,则事件A在一次试验中发生的概率为( )
 ,则事件A在一次试验中发生的概率为( )
,则事件A在一次试验中发生的概率为( )
A .  B .
B .  C .
C . 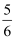 D .
D . 
 B .
B .  C .
C . 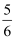 D .
D . 
某地为了解高三学生运动量是否达标,随机抽取了200名同学进行调查,得到数据如下:在120名男生中,运动量达标的有60人;在80名女生中,运动量未达标的有50人.
-
(1) 完成下面的列联表,并判断是否有
 的把握认为运动量达标与性别有关.
的把握认为运动量达标与性别有关. 运动量达标
运动量未达标
合计
男生人数
女生人数
合计
-
(2) 以上述数据样本来估计总体,现从该地的所有高三学生(人数众多)中逐一随机抽取3人,记这3人中运动量达标的男生人数为随机变量X , 若每次抽取的结果是相互独立的,求X的分布列和数学期望.
参考公式与数据:
 ,其中
,其中  .
.
0.100
0.050
0.025
0.010
0.005

2.706
3.841
5.024
6.635
7.879
某机构的招聘面试有3道难度相当的问题,假设小明答对每个问题的概率都是0.6.按照规则,每位面试者共有3次机会,一旦答对所抽到的问题,则面试通过,否则继续抽取下一个问题,依次类推,直到第3个问题为止.用G表示答对问题,用B表示答错问题,假设问题是否答对相互之间不影响.
-
(1) 请写出这个面试的样本空间;
-
(2) 求小明不能通过面试的概率.
将8株某种果树的幼苗分种在4个坑内,每坑种2株,每株幼苗成活的概率为0.5.若一个坑内至少有1株幼苗成活,则这个坑不需要补种,若一个坑内的幼苗都没成活,则这个坑需要补种,每补种1个坑需15元,用X表示补种费用.
-
(1) 求一个坑不需要补种的概率;
-
(2) 求4个坑中恰有2个坑需要补种的概率;
-
(3) 求X的数学期望.
2022年是中国共产主义青年团建团100周年.100年栉风沐雨,共青团始终坚定不移跟党走,团结带领共青团员和广大青年前赴后继、勇当先锋,书写了中国青年运动的华章.实践证明,共青团不愧为党和人民事业的生力军和突击队,不愧为党的得力助手和可靠后备军.为庆祝共青团建团100周年,我校举行团史知识竞赛活动,比赛共20道题,答对一题得5分,答错一题扣2分,学生李华参加了这次活动,假设每道题李华能答对的概率都是 , 且每道题答对与否相互独立.
, 且每道题答对与否相互独立.
 , 且每道题答对与否相互独立.
, 且每道题答对与否相互独立.
-
(1) 求李华开始答题后直到第3题才答对的概率:
-
(2) 求李华得分的期望值.
2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市!为迎接冬奥会的到来,某地很多中小学开展了模拟冬奥会赛事的活动,为了深入了解学生在“自由式滑雪”和“单板滑雪”两项活动的参与情况,在该地随机选取了10所学校进行研究,得到如下数据:

-
(1) 在这10所学校中随机选取3所来调查研究,求这3所学校参与“自由式滑雪”都超过40人的概率;
-
(2) “单板滑雪”参与人数超过45人的学校可以作为“基地学校”,现在从这10所学校中随机选出3所,记
 为选出可作“基地学校”的学校个数,求X的分布列和数学期望;
为选出可作“基地学校”的学校个数,求X的分布列和数学期望;
-
(3) 现在有一个“单板滑雪”集训营,对“滑行、转弯、停止”这3个动作技巧进行集训,且在集训中进行了多轮测试.规定:在一轮测试中,这3个动作中至少有2个动作达到“优秀”,则该轮测试记为“优秀”.在集训测试中,小明同学3个动作中每个动作达到“优秀”的概率均为
 ,每个动作互不影响且每轮测试互不影响.如果小明同学在集训测试中要想获得“优秀”的次数的平均值达到5次,那么理论上至少要进行多少轮测试?
,每个动作互不影响且每轮测试互不影响.如果小明同学在集训测试中要想获得“优秀”的次数的平均值达到5次,那么理论上至少要进行多少轮测试?
随着社会的发展与进步,人们更加愿意奉献自己的力量,积极参与各项志愿活动.某地单位甲有10名志愿者(其中8名男志愿者,2名女志愿者),单位乙有15名志愿者(其中9名男志愿者,6名女志愿者).若从单位甲任选2名志愿者参加某项活动,则恰是一男一女志愿者的概率为;若从两单位任选一个单位,然后从中随机选1名志愿者参加某项活动,则该志愿者为男志愿者的概率为(以上两空用数字作答).
最近更新
- 有机物分子中,所有原子不可能都在同一平面上的是() A.
- 人体内有免疫系统,它是人体抵御病原体侵犯最重要的保卫系统,下列有关叙述正确的是 A.吞噬细胞和淋巴细胞属于免疫细胞 B.
- 某学者描述中国史上的一种制度是:“虽无相名,实有相职,既有相职,却无相权,既无相权,却有相实。”这种制度是指 A.宗法制
- 读“下列天象景观照片”,完成下列问题。(1)照片A、B、C、D所展示的主要天体类型分别是什么?(2)2005年7月4日,
- 中国服饰在不同历史时期特征各异,如商的“威严庄重”,周的“秩序井然”,战国的“清新”,汉的“凝重”,六朝的“清瘦”,唐的
- 在括号内填入适当的整式,使等式成立: = ;
- “非学无以广才,非志无以成学。”肖志国由一个儿时捕捉萤火虫、怀揣无限遐想的孩子,历经求学苦读、艰辛探索,研发出第一代性能
- 图3所示的实例中,目的是为了增大压强的是 图3
- 我国面积最大的省级行政区的简称是( ) A.新 B.沪 C.蜀 D.藏
- 已知数列{an}满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则当n≥2时,an的值为A.
- (21)某突发事件,在不采取任何预防措施的情况下发生的概率为0.3,一旦发生,将造成400万元的损失.现有甲、乙两种相互
- 下图为我国西北地区土地荒漠化扩大的人为因素示意图。读图回答问题影响因素中比重最大的是 A.过度樵采 B.过度放牧
- 下列结构中存在突触的是( ) ① 一个神经元内 ②脊髓 ③大脑皮层 ④树突→轴突
- D1 如图,长方体中,,点E是AB的中点. (1)证明:平面 C1 (2)证明: A1 (3)求二面角的正
- If you can’t get to sleep,get up and try to do something
- 如图2,小物块A位于光滑的斜面上,斜面位于光滑的水平面上,从地面上看,在小物块沿斜面下滑的过程中,斜面对小物块的作用力A
- 14.阅读下面这首诗,然后回答问题。(8分) 望江南 超然台作 苏 轼 春未老,风细柳斜斜。试上超然台上看,半壕
- 用图中装置进行实验,实验一段时间后,现象与预测不一致的是( ) A.A B.B
- It is not polite to enter others’ rooms knocking on
- 湿地有“地球之肾”之称,也是鸟类集中的栖息地,越来越被人们所关注。分析“长江中游湿地50年的变迁”图(阴影部分表示湿地)
 级
级 级
级 级
级


