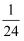4.1 二项分布 知识点题库
两个实习生每人加工一个零件.加工为一等品的概率分别为  和
和  ,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
 和
和  ,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
A .  B .
B . 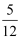 C .
C .  D .
D . 
 B .
B . 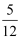 C .
C .  D .
D . 
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6、0.5、0.5、0.4,各人是否需使用设备相互独立.
-
(1) 求同一工作日至少3人需使用设备的概率;
-
(2) X表示同一工作日需使用设备的人数,求X的数学期望.
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为  ,乙,丙做对的概率分别为m,n(m>n),且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为:
,乙,丙做对的概率分别为m,n(m>n),且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为:
 ,乙,丙做对的概率分别为m,n(m>n),且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为:
,乙,丙做对的概率分别为m,n(m>n),且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为: ξ | 0 | 1 | 2 | 3 |
P | | a | b | |
-
(1) 求至少有一位学生做对该题的概率;
-
(2) 求m,n的值;
-
(3) 求ξ的数学期望.
西安世园会志愿者招骋正如火如荼进行着,甲、乙、丙三名大学生跃跃欲试,已知甲能被录用的概率为  ,甲、乙两人都不能被录用的概率为
,甲、乙两人都不能被录用的概率为 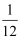 ,乙、丙两人都能被录用的概率为
,乙、丙两人都能被录用的概率为 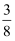 .
.
 ,甲、乙两人都不能被录用的概率为
,甲、乙两人都不能被录用的概率为 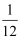 ,乙、丙两人都能被录用的概率为
,乙、丙两人都能被录用的概率为 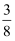 .
.
-
(1) 乙、丙两人各自能被录用的概率;
-
(2) 求甲、乙、丙三人至少有两人能被录用的概率.
从某小组的5名女生和4名男生中任选3人去参加一项公益活动.
-
(1) 求所选3人中恰有一名男生的概率;
-
(2) 求所选3人中男生人数ξ的分布列,并求ξ的期望.
某次考试共有12个选择题,每个选择题的分值为5分,每个选择题四个选项且只有一个选项是正确的,  学生对12个选择题中每个题的四个选择项都没有把握,最后选择题的得分为
学生对12个选择题中每个题的四个选择项都没有把握,最后选择题的得分为  分,
分,  学生对12个选择题中每个题的四个选项都能判断其中有一个选项是错误的,对其它三个选项都没有把握,选择题的得分为
学生对12个选择题中每个题的四个选项都能判断其中有一个选项是错误的,对其它三个选项都没有把握,选择题的得分为  分,则
分,则  的值为( )
的值为( )
 学生对12个选择题中每个题的四个选择项都没有把握,最后选择题的得分为
学生对12个选择题中每个题的四个选择项都没有把握,最后选择题的得分为  分,
分,  学生对12个选择题中每个题的四个选项都能判断其中有一个选项是错误的,对其它三个选项都没有把握,选择题的得分为
学生对12个选择题中每个题的四个选项都能判断其中有一个选项是错误的,对其它三个选项都没有把握,选择题的得分为  分,则
分,则  的值为( )
的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为  .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品. (Ⅰ)随机选取1件产品,求能够通过检测的概率;
(Ⅱ)随机选取3件产品,其中一等品的件数记为 ![]() ,求
,求 ![]() 的分布列;
的分布列;
(Ⅲ)随机选取3件产品,求这三件产品都不能通过检测的概率.
某学生参加一次选拔考试,有5道题,每题10分.已知他解题的正确率为  ,若40分为最低分数线,则该生被选中的概率是( )
,若40分为最低分数线,则该生被选中的概率是( )
 ,若40分为最低分数线,则该生被选中的概率是( )
,若40分为最低分数线,则该生被选中的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某小区超市采取有力措施保障居民正常生活的物资供应.为做好日常生活必需的甲类物资的供应,超市对社区居民户每天对甲类物资的购买量进行了调查,得到了以下频率分布直方图(如图),现从小区超市某天购买甲类物资的居民户中任意选取5户.

(Ⅰ)若将频率视为概率,求至少有两户购买量在  单位:
单位: 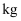 )的概率;
)的概率;
(Ⅱ)若抽取的5户中购买量在  单位:
单位: 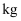 )的户数为2户,从这5户中选出3户进行生活情况调查,记3户中需求量在
)的户数为2户,从这5户中选出3户进行生活情况调查,记3户中需求量在  单位:
单位: 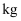 )的户数为ξ,求ξ的分布列和期望.
)的户数为ξ,求ξ的分布列和期望.
某社区为了更好的开展便民服务,对一周内居民办理业务所需要的时间进行统计,结果如下表.假设居民办理业务所需要的时间相互独立,且都是整数分钟.
| 办理业务所需要的时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.3 | 0.4 | 0.1 | 0.1 |
则在某一天,第三位居民恰好等待4分钟才开始办理业务的概率为( )
A . 0.04
B . 0.08
C . 0.17
D . 0.26
随着人民生活水平的提高,人们对牛奶品质要求越来越高,某牛奶企业针对生产的鲜奶和酸奶,在一地区进行了质量满意调查,现从消费者人群中随机抽取500人次作为样本,得到下表(单位:人次):
|
满意度 |
老年人 |
中年人 |
青年人 |
|||
|
酸奶 |
鲜奶 |
酸奶 |
鲜奶 |
酸奶 |
鲜奶 |
|
|
满意 |
100 |
120 |
120 |
100 |
150 |
120 |
|
不满意 |
50 |
30 |
30 |
50 |
50 |
80 |
-
(1) 从样本中任取1个人,求这个人恰好对生产的酸奶质量满意的概率;
-
(2) 从该地区的老年人中抽取2人,青年人中随机选取1人,估计这三人中恰有2人对生产的鲜奶质量满意的概率;
-
(3) 依据表中三个年龄段的数据,你认为哪一个消费群体鲜奶的满意度提升0.1,使得整体对鲜奶的满意度提升最大?(直接写结果).
下列关于说法正确的是( )
A . 抛掷均匀硬币一次,出现正面的次数是随机变量
B . 某人射击时命中的概率为  ,此人射击三次命中的次数
,此人射击三次命中的次数  服从两点分布
C . 小赵.小钱.小孙.小李到4个景点旅游,每人只去一个景点,设事件
服从两点分布
C . 小赵.小钱.小孙.小李到4个景点旅游,每人只去一个景点,设事件  “
“  个人去的景点不相同”,事件
个人去的景点不相同”,事件  “小赵独自去一个景点”,则
“小赵独自去一个景点”,则  D . 抛掷一枚质地均匀的骰子所得的样本空间为
D . 抛掷一枚质地均匀的骰子所得的样本空间为  ,令事件
,令事件  ,事件
,事件  ,则事件A ,
,则事件A ,  独立
独立
 ,此人射击三次命中的次数
,此人射击三次命中的次数  服从两点分布
C . 小赵.小钱.小孙.小李到4个景点旅游,每人只去一个景点,设事件
服从两点分布
C . 小赵.小钱.小孙.小李到4个景点旅游,每人只去一个景点,设事件  “
“  个人去的景点不相同”,事件
个人去的景点不相同”,事件  “小赵独自去一个景点”,则
“小赵独自去一个景点”,则  D . 抛掷一枚质地均匀的骰子所得的样本空间为
D . 抛掷一枚质地均匀的骰子所得的样本空间为  ,令事件
,令事件  ,事件
,事件  ,则事件A ,
,则事件A ,  独立
独立
为大力发展绿色农产品,保证农产品的质量安全,某农业生态园对某种农产品的种植方式进行了甲、乙两种方案的改良,为了检查改良效果,分别在实施甲、乙方案的农场中,各随机抽取60家的该农产品进行检测,并把结果转化为质量指标x(x越小,产品质量越好),所得数据如下表所示.若质量指标满足  ,则认定该农产品为“优质品”,否则认定该农产品为“合格品”.已知此次调查中,实行甲方案的农场中该农产品为“优质品”的农场占20%.
,则认定该农产品为“优质品”,否则认定该农产品为“合格品”.已知此次调查中,实行甲方案的农场中该农产品为“优质品”的农场占20%.
 ,则认定该农产品为“优质品”,否则认定该农产品为“合格品”.已知此次调查中,实行甲方案的农场中该农产品为“优质品”的农场占20%.
,则认定该农产品为“优质品”,否则认定该农产品为“合格品”.已知此次调查中,实行甲方案的农场中该农产品为“优质品”的农场占20%. | x | | | | | |
| 频数 | 5 | 10 | 15 | 60 | 30 |
-
(1) 完成下面列联表,并判断是否有90%的把握认为该农产品为“优质品”与种植方案有关:
甲方案
乙方案
总计
“优质品”农场数
“合格品”农场数
总计
-
(2) 某调研员决定从实施方甲、乙案的所有农场中,随机抽取2家的农产品进行分析,记抽到的农产品是“优质品”的农场数为X,以样本频率作为概率,求X的分布列和数学期望.
附:
 ,其中
,其中  .
.P(K2≥k0)
0.15
0.10
0.05
0.025
k0
2.072
2.706
3.841
5.024
一个盒中装有大小相同的2个黑球,2个白球,从中任取一球,若是白球则取出来,若是黑球则放回盒中,直到把白球全部取出,则在此过程中恰有两次取到黑球的概率为
A .  B .
B .  C .
C . 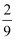 D .
D . 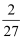
 B .
B .  C .
C . 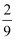 D .
D . 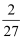
某单位响应“创建国家森林城市”的号召,栽种了甲、乙两种大树各两棵.设甲、乙两种大树的成活率分别为  和
和  ,两种大树成活与否互不影响.
,两种大树成活与否互不影响.
 和
和  ,两种大树成活与否互不影响.
,两种大树成活与否互不影响.
-
(1) 求甲种大树成活两棵的概率;
-
(2) 求甲种大树成活一棵的概率;
-
(3) 求甲、乙两种大树一共成活三棵的概率.
已知随机变量X,Y满足  ,且
,且  ,则
,则  ( )
( )
 ,且
,且  ,则
,则  ( )
( )
A . 2.4
B . 3.4
C . 4.2
D . 4.4
2022年春节后,新冠肺炎的新变种奥密克戎在我国部分地区爆发.该病毒是一种人传人,不易被人们直接发现,潜伏期长且传染性极强的病毒.我们把与该病毒感染者有过密切接触的人群称为密切接触者.一旦发现感染者,社区会立即对其进行流行性病医学调查,找到其密切接触者进行隔离观察.调查发现某位感染者共有10位密切接触者,将这10位密切接触者隔离之后立即进行核酸检测.核酸检测方式既可以采用单样本检测,又可以采用“k合1检测法”.“k合1检测法”是将k个样本混合在一起检测,若混合样本只要呈阳性,则该组中各个样本再全部进行单样本检测;若混合样本呈阴性,则可认为该混合样本中每个样本都是阴性.通过病毒指标检测,每位密切按触者为阴性的概率为 , 且每位密切接触者病毒指标是否为阴性相互独立.
, 且每位密切接触者病毒指标是否为阴性相互独立.
 , 且每位密切接触者病毒指标是否为阴性相互独立.
, 且每位密切接触者病毒指标是否为阴性相互独立.
-
(1) 现对10个样本进行单样本检测,求检测结果最多有2个样本为阳性的概率
 的表达式;
的表达式;
-
(2) 若对10个样本采用“5合1检测法”进行核酸检测.
①求某个混合样本呈阳性的概率;
②设总检测次数为X,求X的分布列和数学期望
 .
.
如图,已知正方体 顶点处有一质点Q,点Q每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同.从一个顶点沿一条棱移动到相邻顶点称为移动一次.若质点Q的初始位置位于点A处,记点Q移动n次后仍在底面ABCD上的概率为
顶点处有一质点Q,点Q每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同.从一个顶点沿一条棱移动到相邻顶点称为移动一次.若质点Q的初始位置位于点A处,记点Q移动n次后仍在底面ABCD上的概率为 , 则下列说法正确的是( )
, 则下列说法正确的是( )
 顶点处有一质点Q,点Q每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同.从一个顶点沿一条棱移动到相邻顶点称为移动一次.若质点Q的初始位置位于点A处,记点Q移动n次后仍在底面ABCD上的概率为
顶点处有一质点Q,点Q每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同.从一个顶点沿一条棱移动到相邻顶点称为移动一次.若质点Q的初始位置位于点A处,记点Q移动n次后仍在底面ABCD上的概率为 , 则下列说法正确的是( )
, 则下列说法正确的是( )
A .  B .
B .  C . 点Q移动4次后恰好位于点
C . 点Q移动4次后恰好位于点 的概率为0
D . 点Q移动10次后仍在底面ABCD上的概率为
的概率为0
D . 点Q移动10次后仍在底面ABCD上的概率为
 B .
B .  C . 点Q移动4次后恰好位于点
C . 点Q移动4次后恰好位于点 的概率为0
D . 点Q移动10次后仍在底面ABCD上的概率为
的概率为0
D . 点Q移动10次后仍在底面ABCD上的概率为
国际排球比赛的规则如下:每场比赛采用“5局3胜制”(即有一支球队先胜3局就获胜,比赛结束).比赛排名采用积分制,积分规则如下:比赛中,以 或
或 取的球队积3分,负队积0分;以
取的球队积3分,负队积0分;以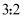 取胜的球队积2分,负队积1分,已知甲、乙两队比赛,甲每局获胜的概率为
取胜的球队积2分,负队积1分,已知甲、乙两队比赛,甲每局获胜的概率为 , 甲、乙两队比赛1场后,设甲队的积分为X,乙队的积分为Y,则
, 甲、乙两队比赛1场后,设甲队的积分为X,乙队的积分为Y,则 的概率为( )
的概率为( )
 或
或 取的球队积3分,负队积0分;以
取的球队积3分,负队积0分;以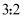 取胜的球队积2分,负队积1分,已知甲、乙两队比赛,甲每局获胜的概率为
取胜的球队积2分,负队积1分,已知甲、乙两队比赛,甲每局获胜的概率为 , 甲、乙两队比赛1场后,设甲队的积分为X,乙队的积分为Y,则
, 甲、乙两队比赛1场后,设甲队的积分为X,乙队的积分为Y,则 的概率为( )
的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
小红、小明、小芳参加技能展示比赛,他们约定用“石头、剪子、布”的方式确定出场的先后顺序.问在1个回合中3个人都出“布”的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- _____ around Zhongshan Park, the tourists were taken to visi
- H7N9 controland prevention is a________to China as well as t
- 被虫蛀过的种子,一般不能萌发的原因是()。 A.种子被细菌感染 B.种子的胚被咬坏 C.种皮被破坏
- X元素最高价氧化物对应的水化物为H3XO4,则它对应的气态氢化物为( ) A.HX B.H2X
- 对于柯尔贝反应RCOOK+H20R—R+H2↑+CO2↑+KOH(R为烃基),下列说法正确的是( ) A.含氢元素
- 下列说法正确的是( ) A.原子最外层电子数为2的元素一定处于周期表第ⅡA族 B.主族元素X、Y能形成XY2型化合物
- 下列反应肯定不属于氧化还原反应的是 A.化合反应 B.分解反应 C.置换反应 D.复分解反应
- A+、B2—、C— 三种离子具有相同的电子层结构,以下比较中正确的是
- Was it in the village _______ we used to live _______ the a
- 某人面北而立,左为东半球,右为西半球,前为热带地区,后为温带地区,其位置是( )。
- 下列溶液中各微粒的浓度关系正确的是A.等pH值的氨水、KOH溶液、Ba(OH)2溶液中:c(NH4+)=c(K+)=2c
- 某溶液中投入铝片后有大量H2放出,则溶液中不可能大量存在的离子是A.Cl- B.H+
- 书面表达 袁隆平被称为“杂交水稻之父”。由于他的努力,中国的水稻产量大幅度提高。请根据以下提示对他进行介绍。 提示:F
- 阅读下面这首宋诗,然后回答问题。 金陵驿二首(其一) 文天祥 草合离宫转夕晖,孤云飘泊复何依? 山河风景元无异,城郭人
- 写作(50分)以“胜过金”为题,写一篇文章。要求:(1)请将题目补充完整。例如 “承诺”、“诚信”、“心静”、“智慧”、
- 下列计算中,结果正确的是( ▲ ) A. B. C. D.
- 下列实验现象的描述中,正确的是 A.红磷在氧气中剧烈燃烧,生成大量白色烟雾 B.水通电后,正极产生氧气,负极
- 面对严峻的就业形势,许多大学生通过到农村就业、到民营企业就业、自主创业等形式,主动破解就业难题。这给我们未来择业的启示是
- 右图是某海区海水表层等温线示意图。图中纵横直线表示经纬线, 曲线表示海水等温线(单位:℃),箭头表示洋流流向。读图回答
- Have you ever had a troubling problemthat has left you wonde