4.1 二项分布 知识点题库
某班学生在一次月考中数学不及格的占16%,语文不及格的占7%,两门都不及格的占4%,已知该班某学生在月考中语文不及格,则该学生在月考中数学不及格的概率是( )
A .  B .
B . 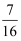 C .
C .  D .
D . 
 B .
B . 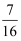 C .
C .  D .
D . 
汽车租赁业被称为“朝阳产业”,因为它具有无须办理保险、无须年检维修、车型可随意更换等优点,以租车代替买车来控制陈本,正慢慢受到国内企事业单位和个人用户的青睐,可以满足人民群众个性化出行、商务活动需求和保障重大社会活动.2013年国庆长假期间某汽车租赁公司为了调查P、Q两种车型的出租情况,现随机抽取了这两种车型各100辆,分别统计了每辆车某个星期内的出租天数,统计数据如表:
P型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
Q型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
-
(1) 根据一周内的统计数据,预测该公司一辆P型车,一辆Q型车一周内合计出租天数恰好为4天的概率;
-
(2) 如果两种车型每辆车每天出租获得的利润相同,该公司需要从P、Q两种车型中购买一辆,请你给出建议应该购买哪一种车型,并说明理由.
甲和乙参加有奖竞猜闯关活动,活动规则:①闯关过程中,若闯关成功则继续答题;若没通关则被淘汰;②每人最多闯3关;③闯第一关得10万奖金,闯第二关得20万奖金,闯第三关得30万奖金,一关都没过则没有奖金.已知甲每次闯关成功的概率为  ,乙每次闯关成功的概率为
,乙每次闯关成功的概率为 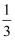 .
.
 ,乙每次闯关成功的概率为
,乙每次闯关成功的概率为 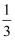 .
.
-
(1) 设乙的奖金为ξ,求ξ的分布列和数学期望;
-
(2) 求甲恰好比乙多30万元奖金的概率.
清华大学自主招生考试题中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如下表:
|
题 |
A |
B |
C |
|
答卷数 |
180 |
300 |
120 |
(Ⅰ)负责招生的教授为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)测试后的统计数据显示,A题的答卷得优的有60份,若以频率作为概率,在(Ⅰ)问中被抽出的选择A题作答的答卷中,记其中得优的份数为  ,求
,求  的分布列及其数学期望
的分布列及其数学期望  .
.
面对H1N1病毒,各国医疗科研机构都在研究疫苗,现有A、B、C三个独立的研究机构在一定的时期内能研制出疫苗的概率分别是  、
、  、
、  .求:
.求:
 、
、  、
、  .求:
.求:
-
(1) 他们都研制出疫苗的概率;
-
(2) 他们都失败的概率;
-
(3) 只有一个机构研制出疫苗的概率;
-
(4) 至多有一个机构研制出疫苗的概率.
甲、乙两人参加“社会主义价值观”知识竞赛,两人获一等奖的概率分别为  和
和  ,若两人是否获得一等奖相互独立,则这两人中恰有一人获得一等奖的概率为.
,若两人是否获得一等奖相互独立,则这两人中恰有一人获得一等奖的概率为.
 和
和  ,若两人是否获得一等奖相互独立,则这两人中恰有一人获得一等奖的概率为.
,若两人是否获得一等奖相互独立,则这两人中恰有一人获得一等奖的概率为.
设随机变量  ,且
,且  ,则n为( )
,则n为( )
 ,且
,且  ,则n为( )
,则n为( )
A . 4
B . 6
C . 8
D . 10
某学校有戏曲和书法两个国学文化校本课程班,高二一班有四名学生报名,每人必须且只能报一个班,每个人报名戏曲班的概率都是  ,用
,用  分别表示这4个人中参加戏曲和书法班的人数.
分别表示这4个人中参加戏曲和书法班的人数.
 ,用
,用  分别表示这4个人中参加戏曲和书法班的人数.
分别表示这4个人中参加戏曲和书法班的人数.
-
(1) 求4个人都报名书法班的概率;
-
(2) 求
 和
和  ;
;
-
(3) 记
 ,求随机变量
,求随机变量  的分布列与数学期望
的分布列与数学期望  .
.
为了普及安全教育,某校组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,甲、乙两班代表队狭路相逢,假设甲队每人回答问题正确的概率均为  ,乙队每人回答问题正确的概率分别为
,乙队每人回答问题正确的概率分别为  ,
,  ,
,  ,且两队各人回答问题正确与否互不影响,则乙队总得分为3分的概率是,甲队总得分为2分且乙队总得分为3分的概率是.
,且两队各人回答问题正确与否互不影响,则乙队总得分为3分的概率是,甲队总得分为2分且乙队总得分为3分的概率是.
 ,乙队每人回答问题正确的概率分别为
,乙队每人回答问题正确的概率分别为  ,
,  ,
,  ,且两队各人回答问题正确与否互不影响,则乙队总得分为3分的概率是,甲队总得分为2分且乙队总得分为3分的概率是.
,且两队各人回答问题正确与否互不影响,则乙队总得分为3分的概率是,甲队总得分为2分且乙队总得分为3分的概率是.
设每个工作日甲、乙两人需使用某种设备的概率分别为0.4、0.5,各人是否需使用设备相互独立,则同一工作日至少1人需使用这种设备的概率为( )
A . 0.3
B . 0.5
C . 0.7
D . 0.9
某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果,某采购商从采购的一批水果中随机抽取100个,利用水果的等级分类标准得到的数据如下:
|
等级 |
标准果 |
优质果 |
精品果 |
礼品果 |
|
个数 |
10 |
30 |
40 |
20 |
-
(1) 若将频率视为概率,从这100个水果中有放回地随机抽取3个,求恰好有2个水果是礼品果的概率;(结果用分数表示)
-
(2) 用分层抽样的方法从这100个水果中抽取10个,再从抽取的10个水果中随机抽取2个,若
 表示抽到的精品果的数量,求
表示抽到的精品果的数量,求  的分布列和期望.
的分布列和期望.
排球比赛的规则是5局3胜制(5局比赛中,先取得3局胜利的一方,获得最终胜利,无平局),在某次排球比赛中,甲队在每局比赛中获胜的概率都相等,均为  ,前2局中乙队以2:0领先,则最后乙队获胜的概率是.
,前2局中乙队以2:0领先,则最后乙队获胜的概率是.
 ,前2局中乙队以2:0领先,则最后乙队获胜的概率是.
,前2局中乙队以2:0领先,则最后乙队获胜的概率是.
 、
、 是治疗同一种疾病的两种新药,某研发公司用若干试验组进行对比试验.每个试验组由4只小白鼠组成,其中2只服用
是治疗同一种疾病的两种新药,某研发公司用若干试验组进行对比试验.每个试验组由4只小白鼠组成,其中2只服用 , 另2只服用
, 另2只服用 , 然后观察疗效.若在一个试验组中,服用
, 然后观察疗效.若在一个试验组中,服用 有效的小白鼠的只数比服用
有效的小白鼠的只数比服用 有效的多,就称该试验组为优类组.设每只小白鼠服用
有效的多,就称该试验组为优类组.设每只小白鼠服用 有效的概率为
有效的概率为 , 服用
, 服用 有效的概率为
有效的概率为 .
.
-
(1) 求一个试验组为优类组的概率;
-
(2) 观察3个试验组,用
 表示这3个试验组中优类组的个数,求
表示这3个试验组中优类组的个数,求 的分布列和数学期望.
的分布列和数学期望.
甲、乙、丙、丁4名棋手进行象棋比赛,赛程如下面的框图所示,其中编号为 的方框表示第
的方框表示第 场比赛,方框中是进行该场比赛的两名棋手,第
场比赛,方框中是进行该场比赛的两名棋手,第 场比赛的胜者称为“胜者
场比赛的胜者称为“胜者 ”,负者称为“负者
”,负者称为“负者 ”,第6场为决赛,获胜的人是冠军.已知甲每场比赛获胜的概率均为
”,第6场为决赛,获胜的人是冠军.已知甲每场比赛获胜的概率均为  , 而乙、丙、丁相互之间胜负的可能性相同.
, 而乙、丙、丁相互之间胜负的可能性相同.
 的方框表示第
的方框表示第 场比赛,方框中是进行该场比赛的两名棋手,第
场比赛,方框中是进行该场比赛的两名棋手,第 场比赛的胜者称为“胜者
场比赛的胜者称为“胜者 ”,负者称为“负者
”,负者称为“负者 ”,第6场为决赛,获胜的人是冠军.已知甲每场比赛获胜的概率均为
”,第6场为决赛,获胜的人是冠军.已知甲每场比赛获胜的概率均为  , 而乙、丙、丁相互之间胜负的可能性相同.
, 而乙、丙、丁相互之间胜负的可能性相同.
(Ⅰ)求甲获得冠军的概率;
(Ⅱ)求乙进入决赛,且乙与其决赛对手是第二次相遇的概率.
惠州市某高中学校组织航天科普知识竞赛,分小组进行知识问题竞答.甲乙两个小组分别从6个问题中随机抽取3个问题进行回答,答对题目多者为胜.已知这6个问题中,甲组能正确回答其中4个问题,而乙组能正确回答每个问题的概率均为 .甲、乙两个小组的选题以及对每题的回答都是相互独立,互不影响的.
.甲、乙两个小组的选题以及对每题的回答都是相互独立,互不影响的.
 .甲、乙两个小组的选题以及对每题的回答都是相互独立,互不影响的.
.甲、乙两个小组的选题以及对每题的回答都是相互独立,互不影响的.
-
(1) 求甲小组至少答对2个问题的概率;
-
(2) 若从甲乙两个小组中选拔一组代表学校参加全市决赛,请分析说明选择哪个小组更好?
某班在一次以“弘扬伟大的抗疫精神,在抗疫中磨炼成长”为主题的班团活动中,拟在2名男生和4名女生这六名志愿者中随机选取3名志愿者分享在参加抗疫志愿者活动中的感悟,则所选取的3人中女生人数的均值为( )
A . 1
B . 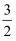 C . 2
D .
C . 2
D . 
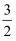 C . 2
D .
C . 2
D . 
某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为  ,且
,且  .记该棋手连胜两盘的概率为p,则( )
.记该棋手连胜两盘的概率为p,则( )
 ,且
,且  .记该棋手连胜两盘的概率为p,则( )
.记该棋手连胜两盘的概率为p,则( )
A . p与该棋手和甲、乙、丙的此赛次序无关
B . 该棋手在第二盘与甲比赛,p最大
C . 该棋手在第二盘与乙比赛,p最大
D . 该棋手在第二盘与丙比赛,p最大
足球比赛淘汰赛阶段常规比赛时间为90分钟,若在90分钟结束时进球数持平,需进行30分钟的加时赛,若加时赛仍是平局,则采用“点球大战”的方式决定胜负.“点球大战”的规则如下:①两队各派5名队员,双方轮流踢点球,累计进球个数多者胜;②如果在踢满5轮前,一队的进球数已多于另一队踢满5轮最多可能射中的球数,则不需要再踢(例如:第4轮结束时,双方“点球大战”的进球数比为2:0,则不需要再踢第5轮了);③若前5轮“点球大战”中双方进球数持平,则从第6轮起,双方每轮各派1人罚点球,若均进球或均不进球,则继续下一轮,直到出现一方进球另一方不进球的情况,进球方胜出.
-
(1) 假设踢点球的球员等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也只有
 的可能性将球扑出,若球员射门均在门内,在一次“点球大战”中,求门将在前三次扑出点球的个数
的可能性将球扑出,若球员射门均在门内,在一次“点球大战”中,求门将在前三次扑出点球的个数 的分布列和期望:
的分布列和期望:
-
(2) 现有甲、乙两队在半决赛中相遇,常规赛和加时赛后双方战平,需进行“点球大战”来决定胜负,设甲队每名队员射进点球的概率均为
 , 乙队每名队员射进点球的概率均为
, 乙队每名队员射进点球的概率均为 , 假设每轮点球中进球与否互不影响,各轮结果也互不影响.
, 假设每轮点球中进球与否互不影响,各轮结果也互不影响.(i)若甲队先踢点球,求在第3轮结束时,甲队踢进了3个球(不含常规赛和加时赛进球)并胜出的概率;
(ii)求“点球大战”在第6轮结束,且乙队以5:4(不含常规赛和加时赛得分)胜出的概率.
为了使更多人参与到冰雪运动中,某校组织了一次简易冰壶比赛.每场比赛由两支队伍对抗进行,每队由2名成员组成,共进行3局.每局比赛时,两队成员交替发球,每名成员只能从发球区( 左侧)掷冰壶一次.当所有成员全部掷完冰壶后,开始计分.若冰壶未到达营垒区,计
左侧)掷冰壶一次.当所有成员全部掷完冰壶后,开始计分.若冰壶未到达营垒区,计 分;若冰壶能准确到达营垒区,计2分,整场比赛累计得分多者获得比赛胜利.已知
分;若冰壶能准确到达营垒区,计2分,整场比赛累计得分多者获得比赛胜利.已知 队两名成员甲、乙每次将冰壶投掷到营垒区的概率分别为
队两名成员甲、乙每次将冰壶投掷到营垒区的概率分别为 和
和 ,
,  队两名成员丙、丁每次将冰壶投掷到营垒区的概率均为
队两名成员丙、丁每次将冰壶投掷到营垒区的概率均为 .假设两队投掷的冰壶在运动过程中无碰撞,每名成员投掷冰壶相互独立,每局比赛互不影响.
.假设两队投掷的冰壶在运动过程中无碰撞,每名成员投掷冰壶相互独立,每局比赛互不影响.
 左侧)掷冰壶一次.当所有成员全部掷完冰壶后,开始计分.若冰壶未到达营垒区,计
左侧)掷冰壶一次.当所有成员全部掷完冰壶后,开始计分.若冰壶未到达营垒区,计 分;若冰壶能准确到达营垒区,计2分,整场比赛累计得分多者获得比赛胜利.已知
分;若冰壶能准确到达营垒区,计2分,整场比赛累计得分多者获得比赛胜利.已知 队两名成员甲、乙每次将冰壶投掷到营垒区的概率分别为
队两名成员甲、乙每次将冰壶投掷到营垒区的概率分别为 和
和 ,
,  队两名成员丙、丁每次将冰壶投掷到营垒区的概率均为
队两名成员丙、丁每次将冰壶投掷到营垒区的概率均为 .假设两队投掷的冰壶在运动过程中无碰撞,每名成员投掷冰壶相互独立,每局比赛互不影响.
.假设两队投掷的冰壶在运动过程中无碰撞,每名成员投掷冰壶相互独立,每局比赛互不影响.
-
(1) 求
 队每局得分
队每局得分 的分布列及期望;
的分布列及期望;
-
(2) 若第一局比赛结束后,
 队得1分,
队得1分, 队得4分,求
队得4分,求 队最终获得本场比赛胜利且总积分比
队最终获得本场比赛胜利且总积分比 队高3分的概率.
队高3分的概率.
某高中学校鼓励学生自发组织各项体育比赛活动,甲、乙两名同学利用课余时间进行乒乓球比赛,比赛采用七局四胜制(即有一方先胜四局即获胜,比赛结束).假设每局比赛甲获胜的概率都是 .
.
 .
.
-
(1) 求比赛结束时恰好打了5局的概率;
-
(2) 若甲以3:1的比分领先时,记
 表示到结束比赛时还需要比赛的局数,求
表示到结束比赛时还需要比赛的局数,求 的分布列及期望.
的分布列及期望.
最近更新
- 执手相看泪眼, 。(《雨霖铃》)
- 7......
- 已知点P是抛物线y2=-8x上一点,设P到此抛物线准线的距离是d1,到直线x+y-10=0的距离是d2,则d1+d2的最
- 2010年4月14日青海玉树发生大地震。面对突然的灾难,藏族、汉族及其他各民族群众挺身而出,生死相依,互帮互助,迅速展开
- 台湾出口导向型经济特征比较明显 ( )
- 如下图所示,两小球A和B均带正电q,质量均为m,连接两小球的绝缘细线长为l.当两个小球都静止时,细线OA的张力T1=__
- 已知函数①,②,③,④,⑤,其中二次函数的个数为( ).A.1B.2C.3D.4
- 辨别固体石蜡和脂肪的方法是A.加热熔化后,滴入有酚酞的烧碱溶液共煮 B.加热熔化后,加入碳酸钠溶液共煮C.加热熔化
- 实验室用碳酸钠晶体配制1.00mol•L﹣1的Na2CO3溶液100mL,造成所配溶液浓度偏低的原因是() A. 暴露在
- 1......
- 用1molMnO2和含HCl为4mol的浓盐酸充分反应(共热),在不考虑HCl挥发的情况下,得到的氯气 A. 等于2mo
- 下列计算正确的是 ( ) A. B. C. D.
- 常温常压下,两个容积相同的烧瓶中分别盛满X和Y两种气体,打开开关a,使两烧瓶内的气体相通,最后容器内的压强由大到小的顺序
- 下列有关遗传学知识的叙述中,正确的是 A.一种性状只有一种表现型
- 以下是有关人体生命活动调节方面的问题,请分析回答:(1)当你走在路上,前方突然出现一辆飞速奔驰的车朝你开来,你会赶快躲开
- 设计植物体细胞杂交实验时,如果期望获得性状优良的作物新品种,不需要考虑的是() A.亲本体细胞去除细胞壁 B.选择具有优
- 已知数列{an}的前n项和Sn=a[2-()n-1]-b[2-(n+1)()n-1](n=1,2,…),其中a、b是非零
- 越来越多的个人在网上开店和网上购物,但是人们对网上交易是否应该缴税有不同的认识。对此,正确的认识是 A.应该纳税,因为税
- 下列读音全对的一项是( ) A.循规蹈矩(jù) 擢(zhuó)发难数 人才济济(jǐ) B.毛遂(s
- 在2011年“两会”召开之前,各地的人大代表、政协委员深入基层,广泛了解民意,听取群众呼声,积极酝酿建议、提案,为制定和



