八年级(初二)数学试题
如图,  ,
, 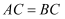 ,
,  于点E,
于点E,  于点D,
于点D,  ,
,  ,则
,则  的长是( )
的长是( )
 ,
, 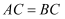 ,
,  于点E,
于点E,  于点D,
于点D,  ,
,  ,则
,则  的长是( )
的长是( ) 
A . 8  B . 4
B . 4  C . 3
C . 3  D . 2
D . 2 
 B . 4
B . 4  C . 3
C . 3  D . 2
D . 2 
货车和轿车分别沿同一路线从A地出发去B地,已知货车先出发10分钟后,轿车才出发,当轿车追上货车5分钟后,轿车发生了故障,花了20分钟修好车后,轿车按原来速度的 继续前进,在整个行驶过程中,货车和轿车均保持各自的速度匀速前进,两车相距的路程y(米)与货车出发的时间x(分钟)之间的关系的部分图象如图所示,对于以下说法:①货车的速度为1500米/分;②
继续前进,在整个行驶过程中,货车和轿车均保持各自的速度匀速前进,两车相距的路程y(米)与货车出发的时间x(分钟)之间的关系的部分图象如图所示,对于以下说法:①货车的速度为1500米/分;② ;③点D的坐标为
;③点D的坐标为 ;④图中a的值是
;④图中a的值是 , 其中正确的结论有( )个
, 其中正确的结论有( )个
 继续前进,在整个行驶过程中,货车和轿车均保持各自的速度匀速前进,两车相距的路程y(米)与货车出发的时间x(分钟)之间的关系的部分图象如图所示,对于以下说法:①货车的速度为1500米/分;②
继续前进,在整个行驶过程中,货车和轿车均保持各自的速度匀速前进,两车相距的路程y(米)与货车出发的时间x(分钟)之间的关系的部分图象如图所示,对于以下说法:①货车的速度为1500米/分;② ;③点D的坐标为
;③点D的坐标为 ;④图中a的值是
;④图中a的值是 , 其中正确的结论有( )个
, 其中正确的结论有( )个
A . 1
B . 2
C . 3
D . 4
如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 185 | 180 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A . 甲
B . 乙
C . 丙
D . 丁
分解因式: .
.
 .
.
已知函数y=ax+b和y=kx的图象交于点P,则根据图象可知,关于x,y的二元一次方程组  的解是.
的解是.
 的解是.
的解是. 
阅读、理解、应用.
例:计算:
解:设 , 则原式
, 则原式 .
.
请你利用上述方法解答下列问题:
-
(1) 计算:
 ;
;
-
(2) 若
 ,
,  , 请比较M,N的大小;
, 请比较M,N的大小;
-
(3) 计算:

如图,△ABC的面积为16,点D是BC边上一点,且BD=  BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )

A . 3
B . 4
C . 5
D . 6
如图,△ABC≌△DEF,若∠A=65° ,则∠EDC的度数为.

计算:(x-y)(x2+xy+y2)=
计算: .
.
 .
.
如图,四边形  内接于
内接于  ,
,  为
为  的直径,
的直径,  .
.
 内接于
内接于  ,
,  为
为  的直径,
的直径,  .
. 
-
(1) 试判断
 的形状,并给出证明;
的形状,并给出证明;
-
(2) 若
 ,
,  ,求
,求  的长度.
的长度.
无论a取何值,点P(a-1,2a-3)都在直线l上,若点Q(m,n)在直线l上,则(2m-n+3)2的值为.
如图所示,直线y=x+2与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,当△CDE周长最小时,点D的坐标为.

如图,已知双曲线y=  与直角三角形OAB的斜边OB相交于D,与直角边AB相交于C. 若BC:CA=2:1,△OAB的面积为8,则△OED的面积为如图,已知双曲线y=
与直角三角形OAB的斜边OB相交于D,与直角边AB相交于C. 若BC:CA=2:1,△OAB的面积为8,则△OED的面积为如图,已知双曲线y=  与直角三角形OAB的斜边OB相交于D,与直角边AB相交于C. 若BC:CA=2:1,△OAB的面积为8,则△OED的面积为( )
与直角三角形OAB的斜边OB相交于D,与直角边AB相交于C. 若BC:CA=2:1,△OAB的面积为8,则△OED的面积为( )
 与直角三角形OAB的斜边OB相交于D,与直角边AB相交于C. 若BC:CA=2:1,△OAB的面积为8,则△OED的面积为如图,已知双曲线y=
与直角三角形OAB的斜边OB相交于D,与直角边AB相交于C. 若BC:CA=2:1,△OAB的面积为8,则△OED的面积为如图,已知双曲线y=  与直角三角形OAB的斜边OB相交于D,与直角边AB相交于C. 若BC:CA=2:1,△OAB的面积为8,则△OED的面积为( )
与直角三角形OAB的斜边OB相交于D,与直角边AB相交于C. 若BC:CA=2:1,△OAB的面积为8,则△OED的面积为( ) 
A .  B . 2
C .
B . 2
C . 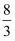 D . 4
D . 4
 B . 2
C .
B . 2
C . 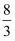 D . 4
D . 4
篮球队5名场上队员的身高(单位:cm)分别是:189,191,193,195,196.现用一名身高为192cm的队员换下身高为196cm的队员,与换人前相比,场上队员的身高( )
A . 平均数变小,方差变小
B . 平均数变小,方差变大
C . 平均数变大,方差变小
D . 平均数变大,方差变大
如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC.若BD=CD,求证:四边形ADCE是矩形.

在如图的计算程序中,y与x之间的函数关系所对应的图象大致是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某商店打算以40元/千克的价格购进一批商品,经市场调查发现,该商品的销售量  (千克)与售价
(千克)与售价  (元)之间的关系如下表:
(元)之间的关系如下表:
 (千克)与售价
(千克)与售价  (元)之间的关系如下表:
(元)之间的关系如下表: | x | 45 | 50 | 55 | 60 | ...... |
| y | 190 | 180 | 170 | 160 | ...... |
-
(1) 求
 关于
关于  的函数关系式;
的函数关系式;
-
(2) 若要控制成本不超过3200元的情况下,保证利润达到3200元,该如何定价?
如果用总长为60m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为p(m),一边长为a(m),那么S,p,a中,常量是( ).
A . a
B . S
C . p
D . p,a
如图所示,点 是菱形
是菱形 对角线的交点,
对角线的交点, ,
,  , 连接
, 连接 , 交
, 交 于点
于点 .
.
 是菱形
是菱形 对角线的交点,
对角线的交点, ,
,  , 连接
, 连接 , 交
, 交 于点
于点 .
. 
-
(1) 求证:四边形
 为矩形;
为矩形;
-
(2) 作
 延长线于点
延长线于点 , 连接
, 连接 , 如果OC:OB=1:2,
, 如果OC:OB=1:2, , 求
, 求 的长.
的长.
最近更新
- 我国境内口前已确认的最早的人类是 ( )A .
- Henry set up a club for football fans, ________ he invited a
- 科学家探索用CO除去SO2,该研究涉及的一个反
- 已知函数 ⑴ 判断函数的单调性,并证明; ⑵
- 已知函数,则__________.
- —Is Mr Brown driving here? —I’m not sure. He _____
- 如图6所示A、B是电容器的两个极板,极是一匀
- (8分)船在400米宽的河中横渡,河水流速是2m
- 下列说法中,不正确的是( ) A.研究物质的性
- 甜菜肉质贮藏根液泡中的花青素使块根呈红色
- I was the middle child of three, and there was a gap of five
- I haven’t seen Ann for ____ long that I’ve forgotten wha
- 鱼缸中装满水,在水中轻轻放入一只小船,小
- 如下图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,
- 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折
- (2010·山东聊城一中高三模块测试) 2
- 能源、信息和材料是现代社会发展的三大支柱
- 读图,回答以下题。 (1)当AB为晨线时,此
- 读右图回答35-36题 35.该水库蓄水的最高水
- 分类法是学习化学的一种方法.下列不属于分



