八年级(初二)数学试题
等腰三角形的底边和腰长分别是10和12,则底边上的高是( )
A . 13
B . 8
C .  D .
D . 
 D .
D . 
如图,在矩形ABCD中,点E是AD上任意一点,则有( )
A . △ABE的周长+△CDE的周长=△BCE的周长
B . △ABE的面积+△CDE的面积=△BCE的面积
C . △ABE∽△DEC
D . △ABE∽△EBC
已知一组数据:21,23,25,25,26,这组数据的平均数和中位数分别是( )
A . 24,25
B . 24,24
C . 25,24
D . 25,25
如图,四边形 内接于
内接于 ,
,  ,
,  为
为 的直径,过D作
的直径,过D作 的切线
的切线 .
.
 内接于
内接于 ,
,  ,
,  为
为 的直径,过D作
的直径,过D作 的切线
的切线 .
.
-
(1) 求证:
 .
.
-
(2) 若
 的半径为5,
的半径为5, , 求
, 求 的长.
的长.
将两块大小相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O.

-
(1) 求证:△BCE≌△B′CF;
-
(2) 当旋转角等于30°时,AB与A′B′垂直吗?请说明理由.
三角形的两边长分别为2cm和9cm,第三边长为奇数,则第三边的长为()
A . 5 cm
B . 7 cm
C . 9 cm
D . 11 cm
如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,则MN的长为 cm.

计算:
-
(1) 2a(a-2a2);
-
(2) (x3)2+(-2x2)3;
-
(3) (2x-1)2-4(x-1)(1+x);
-
(4) (x-2y-1)(x+2y-1).
用直尺和圆规作一个角等于已知角的示意图如图,则要说明  ,需要 证明△
,需要 证明△  ≌△DOC,则这两个三角形全等的依据是(写出全等的简写)
≌△DOC,则这两个三角形全等的依据是(写出全等的简写)
 ,需要 证明△
,需要 证明△  ≌△DOC,则这两个三角形全等的依据是(写出全等的简写)
≌△DOC,则这两个三角形全等的依据是(写出全等的简写)
如图,正比例函数  的图象与反比例函数
的图象与反比例函数 
 在第一象限的图象交于
在第一象限的图象交于  点,过
点,过  点作
点作  轴的垂线,垂足为
轴的垂线,垂足为  ,△
,△  的面积为1.
的面积为1.
 的图象与反比例函数
的图象与反比例函数 
 在第一象限的图象交于
在第一象限的图象交于  点,过
点,过  点作
点作  轴的垂线,垂足为
轴的垂线,垂足为  ,△
,△  的面积为1.
的面积为1. 
-
(1) 求反比例函数的表达式;
-
(2) 如果
 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点  与点
与点  不重合),且
不重合),且  点的横坐标为1,在
点的横坐标为1,在  轴上求一点
轴上求一点  ,使
,使 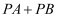 最小.
最小.
以下列各组数据中,能构成直角三角形的是( )
A . 2,3,4
B . 3,4,7
C . 5,12,13
D . 1,2,3
如图,方格纸中每个小正方形的边长均为1, 的顶点和线段
的顶点和线段 的端点均在小正方形的顶点上.
的端点均在小正方形的顶点上.
 的顶点和线段
的顶点和线段 的端点均在小正方形的顶点上.
的端点均在小正方形的顶点上.
⑴在方格纸中面出 , 使
, 使 与
与 关于直线
关于直线 对称(点D在小正方形的顶点上);
对称(点D在小正方形的顶点上);
⑵在方格纸中画出以线段 为一边的平行四边形
为一边的平行四边形 (点G,点H均在小正方形的顶点上),且平行四边形
(点G,点H均在小正方形的顶点上),且平行四边形 的面积为4.连接
的面积为4.连接 , 请直接写出线段
, 请直接写出线段 的长.
的长.
如图,菱形ABCD的面积为12cm2 , 正方形AECF的面积为8cm2 , 则菱形的边长为 cm.

分解因式:2m -32m5=;
如图,在  中,点
中,点  、
、  、
、  的坐标分别为
的坐标分别为  、
、  和
和  ,则当
,则当  的周长最小时,
的周长最小时,  的值为( )
的值为( )
 中,点
中,点  、
、  、
、  的坐标分别为
的坐标分别为  、
、  和
和  ,则当
,则当  的周长最小时,
的周长最小时,  的值为( )
的值为( ) 
A . 0
B . 1
C . 2
D . 3
能把一个三角形分成两个直角三角形的是三角形的( )
A . 高
B . 角平分线
C . 中线
D . 外角平分线
已知点A(4,3)和点B是坐标平面内的两个点,且它们关于过点(-3,0)与y轴平行的直线对称,则点B的坐标是( )
A . (1,3)
B . (-10,3)
C . (4,3)
D . (4,1)
如图,在正方形ABCD中,点G在边AB上(不与点A,B重合),连接DG,作CE⊥DG于点E,AF⊥DG于点F,连接AE,CF.

-
(1) 求证:DE=AF;
-
(2) 若
 设
设  ,求
,求  的值.
的值.
如图:AD=EB,BF=DG,BF∥DG,点A,B,C,D,E在同一直线上.
求证:AF=EG.

如图,在直角坐标系中,有两点  和
和  ,则这两点之间的距离是( )
,则这两点之间的距离是( )
 和
和  ,则这两点之间的距离是( )
,则这两点之间的距离是( ) 
A . 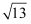 B . 13
C .
B . 13
C .  D . 5
D . 5
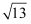 B . 13
C .
B . 13
C .  D . 5
D . 5
最近更新
- 对性腺组织细胞进行荧光标记,等位基因A、a
- 在双曲线中,=.且双曲线与椭圆4x2+9y2=36有公共
- 如图所示,平行板电容器与恒定电源相连,
- 下列句子中加点俗语运用有误的一项是(
- 把除去氧化膜的镁条投入到盛有稀盐酸的试管
- 毛泽东思想被确立为中国共产党的
- 下列关于兴奋沿神经纤维向前传导的叙述中,
- .执行如图所示的程序框图,如果输出,那么
- 先化简,再求值:(﹣)÷,其中x=2.
- 西方学者认为,公元前6—公元前3世纪是人类
- 下图是高中生物有关实验的操作和叙述 ①图
- 某种哺乳动物的直毛(B)对卷毛(b)为显性,黑色
- 制印刷电路版时常用FeCl3溶液作为“腐蚀液”
- 设是实数,则是的 ( ) A.充
- 湖南省所属的温度带和干湿地区是( ) A、
- 如果不等式 无解,那么m的取值范围是( �
- Scientists have found amounts of water molecules inside roc
- 将下列命题用“且”联结成“p∧q”形式的新
- Which do you enjoy ___ your spare time, reading or playing c
- 教育公平是重要的社会公平。今年全国财政安



