七年级(初一)数学：上学期上册　　 下学期下册

七年级(初一)数学下学期下册试题

把下列各数填入它所属的集合内：

3，-200%， $\text{[math]}$ ，|-2|，0，-5.32， $\text{[math]}$ ．

（1）整数集合{…}；
（2）分数集合{…}．
（3）非负数集合{…}．

如图，在平面直角坐标系中，已知点A(2，1)，B(3，－1)，平移线段AB，使点B落在点B₁（－1，－2）处，则点A的对应点A₁的坐标为（）

A . (0，－2) B . （－2，0） C . （0，－4） D . （－4，0）

已知x＞y，则下列不等式不成立的是（　　）

A . x﹣6＞y﹣6 B . 3x＞3y C . ﹣2x＜﹣2y D . ﹣3x+6＞﹣3y+6

$\text{[math]}$ ．

已知 $\text{[math]}$ 与 $\text{[math]}$ 互为相反数．

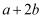（1）求 $\text{[math]}$ 的平方根；
（2）解关于x的方程 $\text{[math]}$

解方程组：

（1） $\text{[math]}$
（2） $\text{[math]}$

一只蚂蚁由（0，0）先向上爬4个单位长度，再向右爬3个单位长度，再向下爬2个单位长度后，它所在位置的坐标是

如图，能判定EB∥AC的条件可以是，也可以是．

关于x、y的方程组 $\text{[math]}$ 的解为整数，则满足这个条件的整数m的个数有（）

A . 4个 B . 3个 C . 2个 D . 无数个

若(x+2019)（x+2018)=1009，则(x+2019)²+(x+2018)²=。

用科学计算器计算： $\text{[math]}$ +2³≈． ( 结果精确到0.01 )

阅读下列解方程组的方法，然后解答问题：

解方程组 $\text{[math]}$ 时，由于x，y的系数及常数项的数值较大，如果用常规的代入消元法、加减消元法来解，不仅计算量大，且易出现运算错误．而采用下面的解法则比较简单：

②﹣①，得3x+3y=3，所以x+y=1，③

③×l4，得l4x+14y=14，④

① ﹣④，得y=2，从而得x=﹣l．

所以原方程组的解是 $\text{[math]}$

请你运用上述方法解方程组： $\text{[math]}$ ．

如图，AB∥CD，EF 分别交AB，CD 于点 J、G.，I为 AB 上一点，连接 FI 交 CD 于点 H，连接GI，若∠EJB=60°，∠IHD=40°，则∠F 的度数为.

图片_x0020_479754867

若点A(2,m)在x轴上，则点B(m-1,m+1)在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

已知关于x的不等式组 $\text{[math]}$ 无解，则m的取值范围是（）

A . m≤3 B . m＞3 C . m＜3 D . m≥3

新定义运算： $\text{[math]}$ ，例如 $\text{[math]}$ ．有以下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④若 $\text{[math]}$ ，则 $\text{[math]}$ ．其中正确的结论有（填序号）．

计算：|﹣3|﹣（5﹣π）⁰+ $\text{[math]}$ ．

布袋中有2个红球.3个黄球，每一个球除颜色外都相同，从袋中任意摸出一个球是黄球的概率是.

若整数 $\text{[math]}$ 同时满足不等式 $\text{[math]}$ 与 $\text{[math]}$ ，则该整数x是（）.

A . 1 B . 2 C . 3 D . 2和3

如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线 $\text{[math]}$ 上一点，则点B与其对应点B′间的距离为．

最近更新

　