七年级(初一)数学下学期下册试题
七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公里化思想.请完成下列证明活动:
-
(1) 活动
 .利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)
.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)
已知:如图,直线
 、
、  被直线
被直线  所截,
所截,  .
.求证:
 .
.证明:假设
 ,则可以过点
,则可以过点  作
作  .
.∵
 ,
,∴
 ().
().∴过
 点存在两条直线
点存在两条直线  、
、  两条直线与
两条直线与  平行,这与基本事实()矛盾.
平行,这与基本事实()矛盾.∴假设不成立.
∴
 .
. -
(2) 活动
 .利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)已知:.
求证:.
证明: .
如果x2=10,则x是一个数,x的整数部分是.
已知,线段  和
和  .用尺规作
.用尺规作  ,使
,使  ,
,  .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)
 和
和  .用尺规作
.用尺规作  ,使
,使  ,
,  .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)

如图,将△ABC沿着点B到点C的方向平移3cm得到△DEF,AB=6cm,BC=9cm,DH=2cm,那么图中阴影部分的面积为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某校设有体育选修课,每位同学必须从羽毛球、篮球、乒乓球、排球、足球五项球类运动中选择一项且只能选择一项球类运动,在该校学生中随机抽取10%的学生进行调查,根据调查结果绘制成如图所示的尚不完整的频数分布表和扇形统计图.
|
运动项目 |
频数 |
|
羽毛球 |
30 |
|
篮球 |
a |
|
乒乓球 |
36 |
|
排球 |
b |
|
足球 |
12 |

请根据以上图、表信息解答下列问题:
-
(1) 频数分布表中的a=,b=;
-
(2) 补全扇形统计图;
-
(3) 排球所在的扇形的圆心角为度;
-
(4) 全校有多少名学生选择参加乒乓球运动?
有下列命题:①两条直线被第三条直线所截,同位角相等;②0.1的算术平方根是0.01;③算术平方根等于它本身的数是1;④如果点 到两坐标轴的距离相等,则
到两坐标轴的距离相等,则 ;⑤若
;⑤若 , 则
, 则 ;⑥若
;⑥若 , 则
, 则 其中假命题的个数是( )
其中假命题的个数是( )
 到两坐标轴的距离相等,则
到两坐标轴的距离相等,则 ;⑤若
;⑤若 , 则
, 则 ;⑥若
;⑥若 , 则
, 则 其中假命题的个数是( )
其中假命题的个数是( )
A . 1个
B . 3个
C . 5个
D . 6个
将一矩形纸片 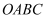 放在直角坐标系中,O为原点,点C在x轴上,点A在Y轴上,
放在直角坐标系中,O为原点,点C在x轴上,点A在Y轴上,  .
.
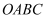 放在直角坐标系中,O为原点,点C在x轴上,点A在Y轴上,
放在直角坐标系中,O为原点,点C在x轴上,点A在Y轴上,  .
. 
-
(1) 如图1,在
 上取一点E,将
上取一点E,将  沿
沿  折叠,使O点落在
折叠,使O点落在  边上的D点处,求直线
边上的D点处,求直线  的解析式;
的解析式;
-
(2) 如图2,在
 边上选取适当的点
边上选取适当的点 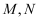 ,将
,将  沿
沿  折叠,使
折叠,使  点落在
点落在  边上的点
边上的点  处,过
处,过  作
作  于点
于点  ,交
,交  于
于  点,连接
点,连接  ,判断四边形
,判断四边形  的形状,并说明理由;
的形状,并说明理由;
-
(3) 、在(2)的条件下,若点
 坐标
坐标  ,点
,点  在
在  直线上,问坐标轴上是否存在点
直线上,问坐标轴上是否存在点  ,使以
,使以  为顶点的四边形是平行四边形,若存在,请直接写出点
为顶点的四边形是平行四边形,若存在,请直接写出点  坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
某工厂要招聘A,B两个工种的工人180人,A,B两个工种的工人的月工资分别为2000元和3000元.现要求B工种的人数不少于A工种人数的2倍.
-
(1) 该工厂招聘A种工人最多多少人?
-
(2) 招聘A工种工人多少人时,可使每月所付的工资总额最少,最少为多少元.
实数a,b在数轴上的位置如图所示,化简|a﹣b|+  =.
=.
 =.
=. ![]()
解方程组: .
.
 .
.
计算:(﹣2)0﹣  =.
=.
 =.
=.
下列调查中,适合用抽样调查的是( )
A . 防疫期间对进入校园的人员进行体温检测
B . 对乘坐高铁的乘客进行安检
C . 调查一批防疫口罩的质量情况
D . 对新研发导弹的零部件进行检查
现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了解学生的视力变化情况,从全市九年级随机抽取了1500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.

解答下列问题:
-
(1) 图中D所在扇形的圆心角度数为 ;
-
(2) 若2015年全市共有30000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
-
(3) 根据扇形统计图信息,你觉得中学生应该如何保护视力?
如图,将三角尺的直角顶点放在直尺的一边上,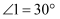 ,
,  , 则
, 则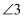 的度数等于( )
的度数等于( )
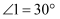 ,
,  , 则
, 则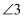 的度数等于( )
的度数等于( ) 
A . 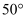 B .
B .  C .
C .  D .
D . 
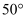 B .
B .  C .
C .  D .
D . 
若点P(m, )关于原点的对称点Q在第三象限,那么m的取值范围是.
)关于原点的对称点Q在第三象限,那么m的取值范围是.
 )关于原点的对称点Q在第三象限,那么m的取值范围是.
)关于原点的对称点Q在第三象限,那么m的取值范围是.
【阅读材料】
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+“是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
-
(1) 【解决问题】
求点A(-2,4),B(
 +
+ -
- )的勾股值[A],[B];
)的勾股值[A],[B]; -
(2) 若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
如图,已知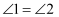 ,
,  , 求
, 求 的度数.
的度数.
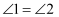 ,
,  , 求
, 求 的度数.
的度数.
已知关于  的一元二次方程
的一元二次方程  ,其中
,其中  ,
,  在数轴上的对应点如图所示,则这个方程的根的情况是( )
在数轴上的对应点如图所示,则这个方程的根的情况是( )
 的一元二次方程
的一元二次方程  ,其中
,其中  ,
,  在数轴上的对应点如图所示,则这个方程的根的情况是( )
在数轴上的对应点如图所示,则这个方程的根的情况是( ) ![]()
A . 有两个不相等的实数根
B . 有两个相等的实数根
C . 无实数根
D . 只有一个实数根
已知  与
与  互为相反数,求
互为相反数,求  的平方根.
的平方根.
 与
与  互为相反数,求
互为相反数,求  的平方根.
的平方根.
先化简,再求值:  ,其中
,其中  ,
,  .
.
 ,其中
,其中  ,
,  .
.
最近更新
- 读图回答:下面的四幅图中,与上图中甲地气候类型相符的是A. B. C.
- 面对就业难,从国家的角度看,解决的根本途径是( ) A.大力发展生产力,促进就业 B.延长退休年龄
- 如图,菱形的边长为,,为的中点,若为菱形内任意一点(含边界),则的最大值为( )A. B.
- To his,the MP4 which hehas had repaired not long before does
- (21) (本小题满分12分) 已知函数的图象过点(-1,-6),且函数的图象关于y轴对称. (Ⅰ)求m、n的值及函数
- 下列说法错误的是( ) A.将一块晶体敲碎后,得到的小颗粒也是晶体 B.固体可以分为晶体和非晶体两类,有些晶体在不同的
- 下列各组元素的原子结构示意图中,具有相似化学性质的一组元素是
- X、Y、Z三种主族元素的单质在常温下都是常见的无色气体,在适当条件下三者之间可以两两发生反应生成物分别是双核、三核和四核
- 已知命题p:∀x∈[1,+∞),lnx>0,那么命题¬p为.
- 完形填空One day, Peter went to see his doctor . “I am always tir
- 下列物质合成时,需要模板的是() A.磷脂和蛋白质 B.DNA和酶 C.性激素和胰岛素D.神经递质和受体
- 18.下面的图表一和图表二,是有关机构对我国不同群体通过电视获取科技信息情况的调查:请根据图表反映的情况,补充下面义段中
- 由熔盐电解法获得的粗铝含有一定量的金属钠和氢气,这些杂质可采用吹气精炼法除去,产生的尾气经处理后可用钢材镀铝。工艺流程如
- 《四川省老年人权益保障条例(修订)》规定:老年人患病住院期间不能自理的,用人单位应当给予独生子女每年累计不超过十五日的护
- 24 ______ for some time after a tiring day is very enjoyabl
- 2015年3月,我国作出把“一带一路”建设与区域开发开放结合起来的决策,并将“一带一路”发展战略列为构筑全方位对外开放新
- 世界上使用人数最多和使用最广泛的语言分别是( ) A、英语和汉语 B、汉语和英语C、俄语和英语
- 北京时间2012年6月16日18时37分神舟九号飞船从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器在轨成功
- 下列函数中,在区间(1,+)上为增函数的是( )A. B. C.
- The job is great _________ salary. It has its disadvantages,



